Библиотека
Теология
Конфессии
Иностранные языки
Другие проекты
|
Ваш комментарий о книге
Мокров Ю. Метрология, стандартизация, сертификация
Глава 4. Погрешности измерений
4.1 Понятие погрешности измерений
Непосредственной задачей измерения является определение значений измеряемой величины. В результате измерения физической величины с истинным значением Хи мы получаем оценку этой величины Хизм. - результат измерений. При этом следует четко различать два понятия: истинные значения физических величин и их эмпирические проявления – действительные значения, которые являются результатами измерений и в конкретной измерительной задаче могут приниматься в качестве истинных значений. Истинное значение величины неизвестно и оно применяют только в теоретических исследованиях.Результаты измерений являются продуктами нашего познания и представляют собой приближенные оценки значений величин, которые находятся в процессе измерений. Степень приближения полученных оценок к истинным (действительным) значениям измеряемых величин зависит от многих факторов: метода измерений, использованных средств измерений и их погрешностей, от свойств органов чувств операторов, проводящих измерения, от условий, в которых проводятся измерения и т.д. Поэтому между истинным значением физической величины и результатом измерений всегда имеется различие, которое выражается погрешностью измерений (то же самое, что погрешностью результата измерений).
Погрешность результата измерения — отклонение результата измерения от истинного (действительного) значения измеряемой величины:
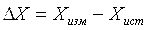
Так как истинное значение измеряемой величины всегда неизвестно и на практике мы имеем дело с действительными значениями величин Хд, то формула для определения погрешности в связи с этим приобретает вид:
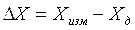
4.2 Модели объекта и погрешности измерений
Задачей измерений является получение значений физической величины, характеризующей соответствующие свойства реального объекта измерений. Однако, вследствие того, что истинное значение измеряемой величины нам неизвестно, возникает вопрос - а что же тогда мы должны измерить? Для ответа на этот вопрос вводится некий идеализированный образ объекта измерений - модель объекта измерений, соответствующие параметры которой можно наилучшим образом представить в качестве истинного значения измеряемой величины. Модель реального объекта измерений обычно представляет собой некоторую его абстракцию и ее определение формируется на основе логических, физических и математических представлений. В качестве примера рассмотрим решение часто рассматриваемой в литературе простейшей измерительной задачи - определение диаметра диска. Реальный объект измерения - диск, представляется его математической моделью - кругом. При этом делается предположение, что диаметр круга идеальным образом отражает то свойство реального диска, которое мы называет его диаметром. По определению диаметр круга одинаков во всех направлениях, поэтому, чтобы проверить соответствие нашей модели реальному объекту (диску), мы должны провести измерения диска в нескольких направлениях. Из полученных результатов измерений могут следовать два вывода.
Если разброс измеренных значений, то есть разности результатов измерений между собой, не превышают заданную в измерительной задаче погрешность измерений диаметра диска, то в качестве результата измерений можно принять любое из полученных значений.
Если же разность результатов измерений превышает заданную погрешность измерений, то это означает, что для данной измерительной задачи принятая модель не подходит и необходимо ввести новую модель объекта измерений. Такой моделью, например, может быть круг, имеющий диаметр, равный наибольшему измеренному значению (описывающий круг).
Другой пример - измерение площади комнаты. Представив пол комнаты в виде прямоугольника, ее площадь можно найти как произведение длины комнаты на ширину. Но если окажется, что ширина комнаты неодинакова по ее длине, то необходимо принять другую модель — например, представить пол комнаты в виде трапеции и определять площадь уже по другой формуле.
Аналогично модели измерений вводится и понятие модели погрешности измерений. Например, деление погрешностей по их происхождению, свойствам, способам выражения и т.д. Так, для выражения случайных погрешностей чаще всего используются вероятностные модели. При этом случайная погрешность характе-ризуется не одним значением, а тем диапазоном значений, в кото-ром она может находиться с определенной вероятностью. Для выбранной модели погрешностей устанавливаются законы ее распределения и те параметры этих распределений, которые являют-ся показателями погрешности, а также статистические методы оценки этих параметров по результатам измерений. Подробнее модели погрешности измерений будут рассмотрены ниже.
4.3 Источники погрешности измерений
Погрешность результата измерения имеет много составляю-щих, каждая из которых обусловлена различными факторами и источниками. Типичный подход к анализу и оцениванию погреш-ностей состоит в выделении этих составляющих, их изучении по отдельности и суммировании по принятым правилам. Определив количественные параметры всех составляющих погрешности и зная способы их суммирования, можно правильно оценить погрешность результата измерений и при возможности скорректировать его с помощью введения поправок.
Ниже приводятся некоторые источники появления погре-ностей измерений:
- неполное соответствие объекта измерений принятой его модели;
- неполное знание измеряемой величины;
- неполное знание влияния условий окружающей среды на измерение;
- несовершенное измерение параметров окружающей среды;
- конечная разрешающая способность прибора или порог его чувствительности;
- неточность передачи значения единицы величины от эталонов к рабочим средствам измерений;
- неточные знания констант и других параметров, используемых в алгоритме обработки результатов измерения;
- аппроксимации и предположения, реализуемые в методе измерений;
- субъективная погрешность оператора при проведении измерений;
- изменения в повторных наблюдениях измеряемой величины при очевидно одинаковых условиях и другие.
Группируя перечисленные выше и другие причины появления погрешностей измерений, их можно разделить на погрешности метода измерений, средств измерений (инструмен-та) и оператора, проводящего измерения. Несовершенство каждо-го этого компонента измерения вносит вклад в погрешность измерения. Поэтому в общем виде погрешность можно выразить следующей формулой:
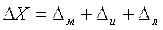
где DМ – методическая погрешность (погрешность метода); DИ - инструментальная погрешность (погрешность средств измерений); DЛ - личная (субъективная) погрешность.
Основные причины возникновения инструментальной погрешности приведены в разделе о средствах измерений.
Методическая погрешность возникает из-за недостатков используемого метода измерений. Чаще всего это является следстви-ем различных допущений при использовании эмпирических зави-симостей между измеряемыми величинами или конструктив-ных упрощений в приборах, используемых в данном методе измерений.
Субъективная погрешность связана с такими индивидуальными особенностями операторов, как внимательность, сосредоточенность, быстрота реакции, степень профессиональной подготовленности. Такие погрешности чаще встречаются при большой доле ручного труда при проведении измерений и почти отсутствуют при использовании автоматизированных средств измерений.
4.4 Классификация погрешностей измерений
Представленная выше классификация погрешностей измерений связана с причинами их возникновения. Кроме этого существуют и другие признаки, по которым классифицируются погрешности.
По характеру проявления (свойствам погрешностей) они разделяются на систематические и случайные, по способам выражения - на абсолютные и относительные.
Абсолютная погрешность выражается в единицах измеряемой величины, а относительная погрешность представляет собой отношение абсолютной погрешности к измеренному (действительному) значению величины и ее численное значение выражается либо в процентах, либо в долях единицы.
Опыт проведения измерений показывает, что при многократ-ных измерениях одной и той же неизменной физической величины при постоянных условиях погрешность измерений можно представить в виде двух слагаемых, которые по-разному проявляются от измерения к измерению. Существуют факторы, постоянно или закономерно изменяющиеся в процессе проведения измерений и влияющие на результат измерений и его погрешность. Погрешности, вызываемые такими факторами, называются систематическими.
Систематическая погрешность – составляющая погреш-ности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. В зависимости от характера изменения систематические погрешности подразделяются на постоянные, прогрессирующие, периодические, изменяющиеся по сложному закону.
Близость к нулю систематической погрешности отражает правильность измерений.
Систематические погрешности обычно оцениваются либо путем теоретического анализа условий измерения, основываясь на известных свойствах средств измерений, либо использованием более точных средств измерений. Как правило, систематические погрешности стараются исключить с помощью поправок. Поправка представляет собой значение величины, вводимое в неисправленный результата измерения с целью исключения систематической погрешности. Знак поправки противоположен знаку величины. На возникновение погрешностей влияют также и факторы, нерегулярно появляющиеся и неожиданно исчезающие. Причем интенсивность их тоже не остается постоянной. Результаты измерения в таких условиях имеют различия, которые индивидуально непредсказуемы, а присущие им закономерности проявляются лишь при значительном числе измерений. Погрешности, появляющиеся в результате действия таких факторов, называются случайными погрешностями.
Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же величины, проведенных с одинаковой тщательностью.
Незначительность случайных погрешностей говорит о хорошей сходимости измерений, то есть о близости друг к другу результатов измерений, выполненных повторно одними и теми же средствами, одним и тем же методом, в одинаковых условиях и с одинаковой тщательностью.
Обнаруживаются случайные погрешности путем повторных измерений одной и той же величины в одних и тех же условиях. Они не могут быть исключены опытным путем, но могут быть оценены при обработке результатов наблюдений. Деление погрешностей измерений на случайные и систематические очень важно, т.к. учет и оценка этих составляющих погрешности требует разных подходов.
Факторы, вызывающие погрешности, как правило, можно свести к общему уровню, когда влияние их на формирование погрешности является более или менее одинаковым. Однако некоторые факторы могут проявляться неожиданно сильно, например, резкое падение напряжения в сети. В таком случае могут возникать погрешности, существенно превышающие погрешности, оправданные условиями измерений, свойствами средств измерений и метода измерений, квалификацией оператора. Такие погрешности называются грубыми, или промахами.
Грубая погрешность (промах) – погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных значений погрешности. Грубые погрешности необходимо всегда исключать из рассмотрения, если известно, что они являются результатом очевидных промахов при проведении измерений. Если же причины появления резко выделяющихся наблюдений установить нельзя, то для решения вопроса об их исключении используют статистические методы. Существует несколько критериев, которые позволяют выявить грубые погрешности. Некоторые из них рассмотрены ниже в разделе об обработке результатов измерений.
4.5 Случайные погрешности
4.5.1 Статистическая устойчивость распределения наблюдений
При наличии случайных погрешностей измерений прибегают к многократным наблюдениям и последующей статистической обработке их результатов. При этом результаты наблюдений и измерений и случайные погрешности рассматриваются как случайные величины, то есть величины, которые характеризуют случайное явление и в результате измерений принимают то или иное значение. Обработка результатов таких наблюдений возможна, если их рассеивание обнаруживает определенные статистические закономерности. Если же результаты наблюдений разбросаны произвольно, то использовать какие-либо способы обработки таких наблюдений и получить результат измерения не представляется возможным.
Поэтому при формулировании конкретной задачи измерений и при получении результатов наблюдений необходимо прежде всего проверить наличие закономерностей в распределении наблюдений. Если такие закономерности обнаруживаются, то распределение наблюдений обладает статистической устойчивостью и для их обработки возможно применение методов теории вероятностей и математической статистики. При этом необходимо отметить, что обнаружение статистических закономерностей в распределении результатов наблюдений проводится после исключения из них всех известных систематических погрешностей.
4.5.2 Дифференциальные и интегральные законы распределения случайной величины
Случайная величина наилучшим и исчерпывающим образом характеризуется в теории вероятностей законом ее распределения. Этот закон устанавливает связь между возможными значениями случайной величины и соответствующими этим значениям вероятностям их появления. Существует две формы описания закона распределения случайной величины - дифференциальная и интегральная. Причем, в метрологии в основном используется дифференциальная форма - закон распределения плотности вероятностей случайной величины.
Дифференциальный закон распределения характеризуется плотностью распределения вероятностей f(x) случайной величины х. Вероятность Р попадания случайной величины в интервал от х1 до х2 при этом дается формулой:

Графически эта вероятность представляет собой отношение площади под кривой f(x) в интервале от х1 до х2 к общей площади, ограниченной всей кривой распределения. Как правило, площадь под всей кривой распределения вероятностей нормируют на единицу.
В данном случае представлено распределение непрерывной случайной величины. Кроме них существуют и дискретные случайные величины, принимающие ряд определенных значений, которые можно пронумеровать.
Интегральный закон распределения случайной величины представляет собой функцию F(x), определяемую формулой
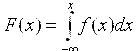
Вероятность, что случайная величина будет меньше х1 дается значением функции F(х) при х = х1 :
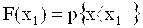
Хотя закон распределения случайных величин является их полной вероятностной характеристикой, нахождение этого закона является довольно трудной задачей и требует проведения многочисленных измерений. Поэтому на практике для описания свойств случайной величины используют различные числовые характеристики распределений. К ним относятся моменты слу-чайных величин: начальные и центральные, которые представляют собой некоторые средние значения. При этом если усредняются величины, отсчитываемые от начала координат, то моменты называются начальными, а если от центра распределения – то центральными.
Начальный момент k-го порядка определяется формулой:
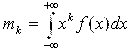
Наибольший практический интерес представляет начальный момент первого порядка - математическое ожидание случайной величины m1 (k=1):
  
Математическое ожидание определяет положение центра группирования случайной величины, вокруг которого наблюдается ее рассеяние. Экспериментальной оценкой математического ожидания при многократных измерениях является среднее арифметическое значение измеряемой величины.
Центральный момент k-го порядка определяется формулой:

Особую роль играет центральный момент второго порядка. Он называется дисперсией D случайной величины и характеризует рассеяние отдельных ее значений:

На практике чаще используется среднее квадратическое отклонение σ (СКО) случайной величины, определяемое формулой:
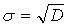
При более подробном изучении распределений случайной величины используются моменты более высоких порядков. Так, любой нечетный центральный момент характеризует асимметрию распределения. Например, третий момент используют для нахождения коэффициента асимметрии кривой распределения относительно математического ожидания. Четвертый центральный момент характеризует остроту вершины кривой распределения.
4.5.3 Характеристики оценки измеряемой величины
Задачей измерения является нахождение по полученным наблюдениям наилучшей оценки измеряемой величины - результата измерения и оценки точности этого результата, т.е. степени его близости к истинному значению величины - погрешности измерений. При этом считается, что закон распределения наблюдений и погрешностей известен. Под оценкой в данном случае понимается нахождение значений параметров этих распределений случайных величин по ограниченному числу наблюдений. Полученные оценки параметров распределений являются лишь приближениями к истинным значениям этих параметров и используются в качестве результата измерений и его погрешности. Для того чтобы оценку, получаемую по результатам многократных наблюдений, можно было использовать в качестве параметра функции распределения случайной величины, она должна отвечать ряду требований — быть состоятельной, несмещенной и эффективной.
Состоятельная оценка – это оценка, которая при увеличении числа наблюдений стремится к истинному значению оцениваемого параметра.
Несмещенная оценка - оценка, математическое ожидание которой равно истинному значению оцениваемого параметра.
Эффективная оценка – оценка, имеющая наименьшую дисперсию по сравнению с любой другой оценкой данного параметра.
Методы нахождения оценок параметров распределений, а по ним результатов измерений и их погрешностей зависят от вида функции распределения и от тех соглашений по обработке результатов измерений, которые нормируются в рамках законодательной метрологии в нормативной документации.
4.5.4 Примеры распределения случайных величин
Способы нахождения значений случайной величины зависят от вида функции ее распределения. Однако на практике такие функции, как правило, неизвестны. Если же случайный характер результатов наблюдений обусловлен погрешностями измерений, то полагают, что наблюдения имеют нормальное распределение. Это обусловлено тем, что погрешности измерений складываются из большого числа небольших возмущений, ни одно из которых не является преобладающим. Согласно же центральной предельной теореме сумма бесконечно большого числа взаимно независимых бесконечно малых случайных величин с любыми распределениями имеет нормальное распределение. Нормальное распределение для 
случайной величины х с математическим ожиданием 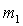 и диспер-сией s имеет вид: и диспер-сией s имеет вид:
Реально даже воздействие ограниченного числа возмущений приводит к нормальному распределению результатов измерений и их погрешностей. В настоящее время наиболее полно разработан математический аппарат именно для случайных величин, имеющих нормальное распределение. Если же предположение о нормальности распределения отвергается, то статистическая обработка наблюдений существенно усложняется и в таком случае невозможно рекомендовать общую методику статистической обработки наблюдений. Часто даже не известно, какая характеристика распределения может служить оценкой истинного значения измеряемой величины.
Выше приведено аналитическое выражение нормального распределения для случайной измеряемой величины х. Переход к нормальному распределению случайных погрешностей 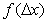 осуществляется переносом центра распределений в осуществляется переносом центра распределений в 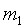 и откладывания по оси абсцисс погрешности и откладывания по оси абсцисс погрешности 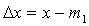 . .
Нормальное распределение характеризуется двумя парамет-рами: математическим ожиданием m1 и средним квадратическим отклонением σ.
При многократных измерениях несмещенной, состоятельной и эффективной оценкой m1 для группы из n наблюдений является среднее арифметическое 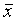 : :
 . .
Нужно сказать, что среднее арифметическое дает оценку математического ожидания результата наблюдений и может быть оценкой истинного (действительного) значения измеряемой величины только после исключения систематических погрешностей.
Оценка S среднего квадратического отклонения (СКО) дается формулой:
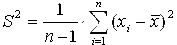
Эта оценка характеризует рассеяние единичных результатов измерений в ряду равноточных измерений одной и той же величины около их среднего значения.
Другими оценками рассеяния результатов в ряду измерений являются размах (разница между наибольшим и наименьшим значением), модуль средней арифметической погрешности (арифметическая сумма погрешностей, деленная на число измерений) и доверительная граница погрешности (подробно рассматривается ниже).
СКО является наиболее удобной характеристикой погрешности в случае ее дальнейшего преобразования. Например, для нескольких некоррелированных слагаемых СКО суммы определяется по формуле:
 . .
Оценка S характеризует рассеяние единичных результатов наблюдений относительно среднего значения, то есть в случае, если мы за результат измерений примем отдельный исправленный результат наблюдений. Если же в качестве результата измерений принимается среднее арифметическое, то СКО этого среднего  определяется по формуле: определяется по формуле:

Нормальное распределение погрешностей имеет следующие свойства:
- симметричность, т.е. погрешности, одинаковые по величине, но противоположные по знаку, встречаются одинаково часто;
- математическое ожидание случайной погрешности равно нулю;
- малые погрешности более вероятны, чем большие;
- чем меньше s, тем меньше рассеяние результатов наблюдений и больше вероятность малых погрешностей.
Другим распространенным в метрологии распределением случайной величины является равномерное распределение - распределение, при котором случайная величина принимает значения в пределах конечного интервала от х1 до х2 с постоянной плотностью вероятностей.
Дифференциальная функция равномерного распределения имеет вид:
f(x) = с при х1 £x£ х2
f(x) = 0 при х2 <x< х1
При нормировке площади кривой распределения на единицу, получаем, что с(х2 – х1) = 1 и с = 1/ (х2 – х1).
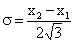 Равномерное распределение характеризуется математичес-ким ожиданием Равномерное распределение характеризуется математичес-ким ожиданием 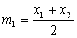 , дисперсией , дисперсией 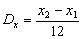 или СКО . или СКО .
Кроме рассмотренных примеров распределений случайных величин существуют и другие важные для практического использования распределения дискретных случайных величин, например, биномиальное распределение и распределение Пуассона. В настоящем курсе они не рассматриваются.
4.5.5 Доверительные интервалы
Приведенные выше оценки параметров распределения случайных величин в виде среднего арифметического для оценки математического ожидания и СКО для оценки дисперсии называются точечными оценками, так как они выражаются одним числом. Однако в некоторых случаях знание точечной оценки является недостаточным. Наиболее корректной и наглядной оценкой случайной погрешности измерений является оценка с помощью доверительных интервалов.
Симметричный интервал в границами ± Δх(Р) называется доверительным интервалом случайной погрешности с довери-тельной вероятностью Р, если площадь кривой распределения между абсциссами –Δх и +Δх составляет Р-ю часть всей площади под кривой плотности распределения вероятностей. При нормировке всей площади на единицу Р представляет часть этой площади в долях единицы (или в процентах). Другими словами, в интервале от -Dх(Р) до +Dх(Р) с заданной вероятностью Р встречаются Р×100% всех возможных значений случайной погрешности.
Доверительный интервал для нормального распределения находится по формуле:
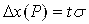
где коэффициент t зависит от доверительной вероятности Р.
Для нормального распределения существуют следующие соотношения между доверительными интервалами и доверительной вероятностью: 1s (Р=0,68), 2s (Р= 0,95), 3s (Р= 0,997), 4s (Р=0,999).
Доверительные вероятности для выражения результатов измерений и погрешностей в различных областях науки и техники принимаются равными. Так, в технических измерениях принята доверительная вероятность 0,95. Лишь для особо точных и ответственных измерений принимают более высокие доверительные вероятности. В метрологии используют, как правило, доверитель-ные вероятности 0,97, в исключительных случаях 0,99. Необходимо отметить, что точность измерений должна соответствовать поставленной измерительной задаче. Излишняя точность ведет к неоправданному расходу средств. Недостаточная точность измерений может привести к принятию по его результатам ошибочных решений с самыми непредсказуемыми последствиями, вплоть до серьезных материальных потерь или катастроф.
При проведении многократных измерений величины х, подчиняющейся нормальному распределению, доверительный интервал может быть построен для любой доверительной вероятности по формуле:
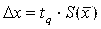
где tq– коэффициент Стьюдента, зависящий от числа наблюдений n и выбранной доверительной вероятности Р. Он определяется с помощью таблицы q-процентных точек распределения Стьюдента, которая имеет два параметра: k = n – 1 и q= 1 – P; 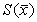 – оценка среднего квадратического отклонения среднего арифметического. – оценка среднего квадратического отклонения среднего арифметического.
Доверительный интервал для погрешности Dх(Р) позволяет построить доверительный интервал для истинного (действи-тельного) значения измеряемой величины , оценкой которой является среднее арифметическое 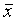 . Истинное значение измеряемой величины находится с доверительной вероятностью Р внутри интервала: . Истинное значение измеряемой величины находится с доверительной вероятностью Р внутри интервала: 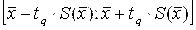 . Доверительный интервал позволяет выяснить, насколько может измениться полученная в результате данной серии измерений оценка измеряемой величины при проведении повторной серии измерений в тех же условиях. Необходимо отметить, что доверительные интервалы строят для неслучайных величин, значения которых неизвестны. Такими являются истинное значение измеряемой величины и средние квадратические отклонения. В то же время оценки этих величин, получаемые в результате обработки данных наблюдений, являются случайными величинами. . Доверительный интервал позволяет выяснить, насколько может измениться полученная в результате данной серии измерений оценка измеряемой величины при проведении повторной серии измерений в тех же условиях. Необходимо отметить, что доверительные интервалы строят для неслучайных величин, значения которых неизвестны. Такими являются истинное значение измеряемой величины и средние квадратические отклонения. В то же время оценки этих величин, получаемые в результате обработки данных наблюдений, являются случайными величинами.
Недостатком доверительных интервалов при оценке случай-ных погрешностей является то, что при произвольно выбираемых доверительных вероятностях нельзя суммировать несколько погреш-ностей, т.к. доверительный интервал суммы не равен сумме довери-тельных интервалов. Суммируются дисперсии независимых случай-ных величин: Då = åDi. То есть, для возможности суммирования составляющие случайной погрешности должны быть представлены своими СКО, а не предельными или доверительными погрешностями.
4.6 Систематические погрешности
Обнаружение и исключение систематических погрешностей представляет собой сложную задачу, требующую глубокого анализа всей совокупности результатов наблюдений, используемых средств, методов и условий измерений. При этом необходимо отметить, что устранение систематических погрешностей осуществляется не путем математической обработки результатов наблюдений, а применением соответствующих методов измерений. В частности, проведением измерений различными независимыми методами или выполнением измерений с параллельным применением более точных средств измерений.
Существуют некоторые специальные приемы проведения измерений, которые позволяют исключить части систематических погрешностей:
- Исключение самого источника погрешностей.
- Замещение измеряемой величины равновеликой ей известной величиной так, чтобы при этом в состоянии и действии всех используемых средств измерений не происходило никаких изменений. Таким путем может быть исключена погрешность компаратора.
- Компенсация погрешности по знаку путем проведения измерений в прямом и обратных направлениях одним и тем же прибором. Например, определяя значение измеряемой величины при подходе к определенной точке шкалы слева и справа от нее и вычисляя среднее значение.
- Наблюдения через период изменения влияющей величины. Это позволяет исключить погрешности, изменяющиеся по периодическому закону.
- Измерения одной величины несколькими независимыми методами с последующим вычислением среднего взвешенного значения измеряемой величины.
- Измерения одной величины несколькими приборами с последующим вычислением среднего арифметического из показаний всех приборов.
Систематические погрешности устраняются путем введения поправок, которые находятся разными путями и представляют собой значения абсолютных погрешностей, которые вычитаются из результата измерений. Так, инструментальные составляющие систематической погрешности находят по результатам поверки средств измерений.
Поправки для учета влияющих величин вычисляют с использованием известных функций или коэффициентов влияния по результатам вспомогательных измерений этих величин. Но введение поправок не исключает полностью систематические погрешности, так как остаются, например, погрешности определения поправок. Эти неисключенные части представляют собой неисключенные остатки систематических погрешностей (НСП).
Так как полностью исключить систематические погрешности невозможно, то возникает задача оценивания границ или других параметров этих погрешностей. Как правило, систематическая погрешность результата измерения оценивается по ее состав-ляющим. Эти составляющие бывают либо известны заранее, либо могут быть определены с помощью вспомогательных данных, например, вычислены для каждой из влияющих величин. В качестве их могут выступать и погрешности определения поправок. Неисключенная систематическая погрешность характеризуется границей каждой ее составляющей.
В связи с этим возникает задача суммирования составляю-щих систематической погрешности. При этом составляющие должны рассматриваться как случайные величины и суммироваться методами теории вероятностей, что предполагает знание функции распределения этих составляющих. Однако, закон распределения элементарных составляющих погрешности, как правило, неизвестен. Поэтому при суммировании руководствуются следующим практи-ческим правилом, основанном на здравом смысле и интуиции:
- если известна оценка границ погрешности, то ее распределение следует считать равномерным;
- если же известна оценка СКО погрешности, распределение следует считать нормальным.
Применение этого правила позволяет статистически суммировать составляющие систематической погрешности. В соответствии с ним при отсутствии дополнительной информации неисключенные остатки систематической погрешности рассматриваются как случайные величины, имеющие равномерное распределение.
Границы неисключенной систематической погрешности Q при числе слагаемых большим или равным 4 вычисляются по формуле:
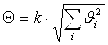
где 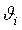 - граница i-ой составляющей погрешности; k - коэффициент, определяемый доверительной вероятностью. При Р = 0,95 k = 1.1, при Р = 0,99 k = 1,4. - граница i-ой составляющей погрешности; k - коэффициент, определяемый доверительной вероятностью. При Р = 0,95 k = 1.1, при Р = 0,99 k = 1,4.
При числе слагаемых меньших или равных 3 значения 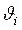 суммируются арифметически по модулю. Если же суммировать НСП арифметически при любом числе слагаемых, то полученная оценка будет хотя и надежной, но завышенной. суммируются арифметически по модулю. Если же суммировать НСП арифметически при любом числе слагаемых, то полученная оценка будет хотя и надежной, но завышенной.
Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что при вычислении доверительных границ случайной погрешности.
4.7 Методы обработки результатов прямых измерений
Основные положения методов обработки результатов прямых измерений с многократными наблюдениями определены в ГОСТ 8.207-76.
За результат измерения принимают среднее арифмети-ческое данных nнаблюдений, из которых исключены систематичес-кие погрешности. При этом предполагается, что результаты наблю-дений после исключения из них систематических погрешностей принадлежат нормальному распределению. Для вычисления резуль-тата измерения следует из каждого наблюдения исключить система-тическую погрешность и получить в итоге исправленный результат i–го наблюдения. Затем вычисляется среднее арифметическое этих исправленных результатов, которое принимается за результат измерения. Среднее арифметическое является состоятельной, несмещенной и эффективной оценкой измеряемой величины при нормальном распределении данных наблюдений.
Следует отметить, что иногда в литературе вместо термина результат наблюдения иногда применяют термин результат отдельного измерения, из которого исключены систематические погрешности. При этом за результат измерения в данной серии из нескольких измерений понимают среднее арифметическое значение. Это не меняет сути излагаемых ниже процедур обработки результатов.
При статистической обработке групп результатов наблюдений следует выполнять следующие операции:
- Исключить из каждого наблюдения известную систематическую погрешность и получить исправленный результат отдельного наблюдения x.
- Вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения:
Т  
- Вычислить оценку
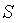 среднего квадратического отклонения среднего квадратического отклонения
группы наблюдений:

Проверить наличие грубых погрешностей – нет ли значений 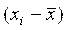 , которые выходят за пределы ±3S. При нормальном законе распределений с вероятностью, практически равной 1 (0,997), ни одно из значений этой разности не должно выйти за указанные пределы. Если они имеются, то следует исключить из рассмотрения соответствующие значения , которые выходят за пределы ±3S. При нормальном законе распределений с вероятностью, практически равной 1 (0,997), ни одно из значений этой разности не должно выйти за указанные пределы. Если они имеются, то следует исключить из рассмотрения соответствующие значения 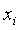 и заново повторить вычисления и заново повторить вычисления 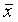 и оценку S. и оценку S.
- Вычислить оценку СКО
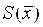 результата измерения (среднего результата измерения (среднего
арифметического)

- Проверить гипотезу о нормальности распределения результатов наблюдений.
Существуют различные приближенные методы проверки нормальности распределения результатов наблюдений. Некоторые из них приведены в ГОСТ 8.207-76. При числе наблюдений меньше 15 в соответствии с этим ГОСТ принадлежность их к нормальному распределению не проверяют. Доверительные границы случайной погрешности определяют лишь в том случае, если заранее известно, что результаты наблюдений принадлежат этому распределению. Приближенно о характере распределения можно судить, построив гистограмму результатов наблюдений. Математические методы проверки нормальности распределения рассматриваются в специальной литературе.
- Вычислить доверительные границы e случайной погрешности (случайной составляющей погрешности) результата измерения
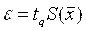
где tq - коэффициент Стьюдента, зависящий от числа наблюдений и доверительной вероятности. Например, при n = 14, P = 0,95 tq = 2,16. Значения этого коэффициента приведены в приложении к указанному стандарту.
- Вычислить границы суммарной неисключенной систематической погрешности (НСП) результата измерений Q (по формулам раздела 4.6).
- Проанализировать соотношение Q и
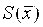 : :
Если 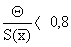 , то НСП по сравнению со случайными погрешностя-ми пренебрегают, и граница погрешности результата D = e.. Если , то НСП по сравнению со случайными погрешностя-ми пренебрегают, и граница погрешности результата D = e.. Если 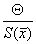 > 8, то случайной погрешностью можно пренебречь и граница погрешности результата D = Θ. Если оба неравенства не выполняются, то границу погрешности результата находят путем построения композиции распределений случайных погрешностей и НСП по формуле: > 8, то случайной погрешностью можно пренебречь и граница погрешности результата D = Θ. Если оба неравенства не выполняются, то границу погрешности результата находят путем построения композиции распределений случайных погрешностей и НСП по формуле: 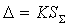 , где К – коэффициент, зависящий от соотношения случайной погрешности и НСП; Så - оценка суммарного СКО результата измерения. Оценку суммарного СКО вычисляют по формуле: , где К – коэффициент, зависящий от соотношения случайной погрешности и НСП; Så - оценка суммарного СКО результата измерения. Оценку суммарного СКО вычисляют по формуле:
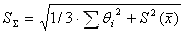 . .
Коэффициент К вычисляют по эмпирической формуле:
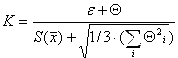 . .
Доверительная вероятность для вычисления 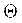 и и 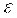 должна быть одной и той же. должна быть одной и той же.
Погрешность от применения последней формулы для композиции равномерного (для НСП) и нормального (для случайной погрешности) распределений достигает 12 % при доверительной вероятности 0,99.
9. Записать результат измерений. Написание результата измерений предусмотрено в двух вариантах, так как следует различать измерения, когда получение значения измеряемой величины является конечной целью, и измерения, результаты которых будут использоваться для дальнейших вычислений или анализа.
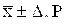 В первом случае достаточно знать общую погрешность результата измерения и при симметричной доверительной погреш-ности результаты измерений представляют в форме: , где В первом случае достаточно знать общую погрешность результата измерения и при симметричной доверительной погреш-ности результаты измерений представляют в форме: , где
где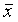 – результат измерения. – результат измерения.
Во втором случае должны быть известны характеристики составляющих погрешности измерения – оценка среднего квадратического отклонения результата измерения 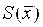 , границы НСП , границы НСП 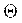 , число выполненных наблюдений , число выполненных наблюдений 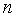 . При отсутствии данных о виде функций распределения составляющих погрешности результата и необходимости дальнейшей обработки результатов или анализа погрешностей, результаты измерений представляют в форме: . При отсутствии данных о виде функций распределения составляющих погрешности результата и необходимости дальнейшей обработки результатов или анализа погрешностей, результаты измерений представляют в форме:
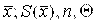
Если границы НСП вычислены в соответствии с п.4.6, то дополнительно указывают доверительную вероятность Р.
Оценки 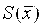 , , 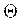 и производные от их величины могут быть выражены как в абсолютной форме, то есть в единицах измеряемой величины, так и относительной, то есть как отношение абсолютного значения данной величины к результату измерения. При этом вычисления по формулам настоящего раздела следует проводить с использованием величин, выраженных только в абсолютной или в относительной форме. и производные от их величины могут быть выражены как в абсолютной форме, то есть в единицах измеряемой величины, так и относительной, то есть как отношение абсолютного значения данной величины к результату измерения. При этом вычисления по формулам настоящего раздела следует проводить с использованием величин, выраженных только в абсолютной или в относительной форме.
4.8 Однократные измерения
В технике большинство измерений являются однократ-ными, т.е. для получения результата измерения используется одно показание прибора. К такому виду относятся, например, измерения при проведении индивидуального дозиметрического контроля, при которых часто используется один детектор. Результат однократного измерения включает в себя все присущие ему погрешности (инструментальную, методическую, субъективную), в каждой из которых могут быть как систематические, так и случайные составляющие. Если при этом необходимо точно оценить погрешность результата измерений, то следует выявить и оценить все составляющие погрешностей и просуммировать их.
Случайная составляющая погрешности не может быть рассчитана по результатам измерения, хотя она неявно присутствует в нем. В качестве оценки случайной составляющей погрешности может быть использован, например, коэффициент вариации, определяемый предварительно в процессе многократных измерений при изучении воспроизводимости показаний данного прибора. Коэффициент вариации находится как отношение оценки среднего квадратического отклонения к среднему арифметическому показа-ний прибора при многократных измерениях. В некоторых случаях случайная погрешность может определяться доверительными границами.
Оценку систематических погрешностей можно получить по характеристикам используемого прибора (по паспортным данным или из свидетельства о поверке) и метода измерения (путем его анализа). Из документации на прибор можно оценить и учесть дополнительные систематические погрешности.
Основные этапы оценки погрешности при однократных измерениях с точным оцениванием погрешности следующие:
- Учитывается систематическая погрешность прибора.
- Оценивается систематическая погрешность метода измерений.
- Оцениваются по документации на прибор дополнительные систематические погрешности, обусловленные влияющими величинами.
- Из отсчета прибора исключаются все известные система-тические погрешности (в соответствии с пп. 1, 2, 3) и опреде-ляется исправленный результат измерения, который содержит НСП и случайные составляющие погрешности.
- Оцениваются границы Qi составляющих НСП, распределение которых принимается равномерным. Ими могут быть, например, погрешности эталонов при поверке СИ, погрешности поправок и т.п. После этого определяются границы Q суммарной НСП по приведенным выше формулам.
- Предварительно перед использованием прибора определяется коэффициент вариации - оценка случайной погрешности, которая используется при последующих однократных измерениях с прибором.
- Сопоставляются оценки НСП и случайной погрешности по критериям предыдущего раздела и при возможности пренебрежения какой-либо из них определяются границы погрешности результата D.
Если необходимо учитывать обе составляющие, то в качестве границы погрешности результата измерения D принимается суммарная средняя квадратическая погрешность Så, , вычисляемая по формуле раздела 4.7 с определением СКО результата измерений и полуэмпирического коэффициента К. Для исключения грубых погрешностей однократное измерение следует повторять 2-3 раза и за результат принимать среднее арифметическое.
На практике часто встречаются измерения, для которых нет необходимости точно оценивать погрешность. В таких измерениях в качестве результата принимают значение отсчета х, а для оценивания погрешности измерения используются предел допускаемой основной погрешности прибора Dпр и дополнительные погрешности прибора Yiот влияющих величин. Субъективные погрешности при этом считаются малыми и ими пренебрегают.
Оценка погрешности результата измерения Då определяется как сумма абсолютных величин основной погрешности и суммарной систематической по формуле:
Då = |Dпр| + å|Yi|.
Более точная оценка погрешности может быть получена статистическим сложением составляющих по формуле раздела 4.7 в предположении их равномерного распределения.
4.9 Определение результатов косвенных измерений и оценивание их погрешностей
Методы обработки результатов косвенных измерений изложены в Методических указаниях РД 50-555-85 «Измерения косвенные. Определение результатов измерений и оценивание их погрешностей».
Основные этапы обработки результатов косвенных измерений следующие.
 1. Искомое значение величины Y находят на основании результатов измерений аргументов x1, …, xi, …, xm, связанных с искомой величиной нелинейной зависимостью . . Вид функ-ции f должен быть известен из теоретических предпосылок или установлен экспериментально. Погрешность неизвестной величины Y зависит от погрешностей измерения аргументов. Ниже рассматри-вается случай, когда аргументы независимы друг от друга. 1. Искомое значение величины Y находят на основании результатов измерений аргументов x1, …, xi, …, xm, связанных с искомой величиной нелинейной зависимостью . . Вид функ-ции f должен быть известен из теоретических предпосылок или установлен экспериментально. Погрешность неизвестной величины Y зависит от погрешностей измерения аргументов. Ниже рассматри-вается случай, когда аргументы независимы друг от друга.
2. Оценка СКО случайной погрешности S(Y) вычисляют по формуле:
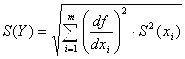
где xi– результат измерения аi-го аргумента; S(xi) – оценка СКО результата измерения xi-го аргумента (определяется по формулам раздела 4.6.7).
3. Доверительные границы случайной погрешности e, при условии, что распределение погрешностей результатов измерений аргументов не противоречит нормальному распределению, определяют по формуле: 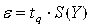
4. Границу неисключенной систематической погрешности резуль-тата измерения вычисляют по формуле
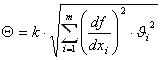
где k – поправочный коэффициент для принятой доверительной вероятности и числа m составляющих НСП, для Р=0,95 коэффициент k = 1,1.
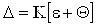 5. Погрешность результата измерения вычисляют в зависимости от соотношения границ НСП и случайной погрешности. При 5. Погрешность результата измерения вычисляют в зависимости от соотношения границ НСП и случайной погрешности. При 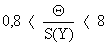 доверительную границу результата косвенного изме-рения D вычисляют по формуле , где К – коэффициент, зависящий от отношения доверительную границу результата косвенного изме-рения D вычисляют по формуле , где К – коэффициент, зависящий от отношения 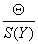 и доверительной вероятности (значения К приведены в указанных РД). и доверительной вероятности (значения К приведены в указанных РД).
6. Результат измерений вычисляется по приведенной выше формуле. Если предполагается исследование и сопоставление результатов измерений или анализ погрешностей, то результат измерения и его погрешность представляют в виде
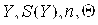 . .
Если границы погрешности результата измерения симмет-ричны, то результат измерения и его погрешность представляют в виде U ± D.
7. При неизвестных распределениях погрешностей измерений аргументов и при наличии корреляции между ними результат косвенного измерения и его погрешность определяются методом приведения, основанном на приведении ряда отдельных значений косвенно измеряемой величины к ряду прямых измерений. Подробно этот метод описан в упомянутых выше РД.
4.10 Записи погрешностей и правила округления
Для единообразия выражения результатов измерений и погрешностей формы их представления стандартизируются. Основные правила при этом следующие.
Так как погрешности определяют лишь зону недостоверности результата измерений, знать их очень точно не требуется. Поэтому в окончательной записи погрешность выражается одной или двумя значащими цифрами. Значащими цифрами числа являются цифры, остающиеся после отбрасывания стоящих впереди нулей. Так, в числах 0,12 и 0,012 находится по две значащие цифры. Принято, что наименьшие разряды числовых значений результата измерений и погрешности должны быть одинаковы: 20,56±0,25 или 2,1±0,1. Одной из самых распространенных ошибок при оценивании результатов и погрешностей измерений является вычисление их с чрезмерно большим числом значащих цифр. Как правило, в этом нет необходимости и только при промежуточных вычислениях можно удерживать по 3-4 значащие цифры.
Лишь при наиболее точных вычислениях оставляют две цифры. Результат измерения должен быть записан так, чтобы он оканчивался десятичным знаком того же разряда, что и значение погрешности. Большее число разрядов не нужно, так как это не уменьшит неопределенности результата, характеризуемого этой погрешностью. Уменьшение же числа разрядов путем округления увеличивает неопределенность результата измерений и уменьшает его точность. Например, погрешность округления погрешности до двух значащих цифр составляет 5 %, а до одной значащей цифры – не более 50 %.
Установлены следующие правила округления результатов и погрешностей измерений:
1. Результат измерения округляется так, чтобы он оканчивался цифрой того же разряда, что и значение его погрешности. Если десятичная дробь в числовом значении результата измерений оканчивается нулями, то их отбрасывают только до того разряда, который соответствует разряду числового значения погрешности. Например, результат 3, 2800 при погрешности 0,001 округляют до 3,280.
2. Если цифра старшего из отбрасываемых разрядов меньше 5, то остающиеся цифры числа не изменяют, лишние цифры в целых числах заменяют нулями, а в десятичных дробях отбрасывают. Например, число 267 245 при сохранении четырех значащих цифр должно быть округлено до 267 200; число 165,245 до165,2.
3. Если цифра старшего отбрасываемого разряда больше или равна 5, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу: 14597®14600; 123,58®124;
4. Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или равны нулю, то последнюю сохраняемую цифру не изменяют, если она четная, и увеличивают, если она нечетная: 10,5®10; 11,5®12.
Ваш комментарий о книге
Обратно в раздел Наука
|
|
