Библиотека
Теология
Конфессии
Иностранные языки
Другие проекты
|
Ваш комментарий о книге
Бирюков С., Чередов А. Метрология: Тексты лекций
3. СРЕДСТВА ИЗМЕРЕНИЙ
-
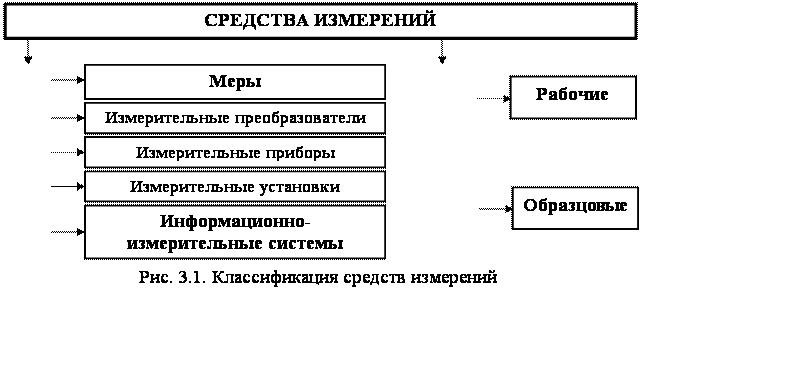
Классификация средств измерений
Средства измерений - технические средства, используемые при измерениях и имеющие нормированные метрологические свойства.
По назначению средства измерений разделяют на меры, измерительные преобразователи, измерительные приборы, измерительные установки и измерительные системы (рис. 3.1) [1]. По метрологическому назначению средства измерений делят на образцовые и рабочие [4].
Образцовые средства измерений предназначены для поверки по ним как рабочих, так и образцовых средств измерений менее высокой точности. Процесс передачи размера единиц от образцовых средств измерений высшей точности рабочим и образцовым средствам измерений более низкой точности
представляет собой поверку средств измерений, поэтому все образцовые средства измерения являются средствами поверки.
Рабочие средства измерений применяются для измерений, не связанных с передачей размера единиц. Они предназначены для измерений размеров величин, необходимых в разнообразной деятельности человека.
Каждое средство измерения должно применяться только по своему прямому назначению. Не разрешается применять рабочие средства измерений для проведения поверочных работ; точно так же запрещается использование образцовых средств для измерений, не связанных с поверкой.
Запрещение применять образцовые средства измерений для практических измерений - одно из важнейших требований метрологии. Однако им нередко пренебрегают или недооценивают его значение. Каким бы точным не было бы средство измерений, применяемое для практических измерений, его нельзя использовать для поверки других средств измерений. Само оно должно поверяться по образцовому средству измерений, имеющему более высокую точность [4].
Мерой называется средство измерений, предназначенное для воспроизведения физической величины заданного размера. Примерами мер являются аттенюаторы - меры затухания, магазины сопротивлений - меры сопротивления, измерительные генераторы — меры напряжения (мощности) и частоты сигналов и т.д. К мерам относятся также образцы и образцовые вещества [6].
Существуют однозначные и многозначные (переменные) меры (рис. 3.2). Мера, воспроизводящая физическую величину одного размера, называется однозначной, например, гиря, плоскопараллельная концевая мера длины, измерительная колба, мера ЭДС. - нормальный элемент, конденсатор постоянной емкости. Величины, для которых операция сложения выполняется сравнительно легко, воспроизводятся с помощью многозначных или однозначных мер, объединяемых в наборы или магазины мер [4].
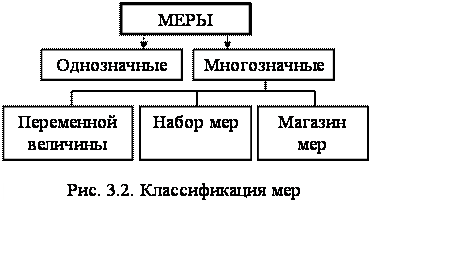
Мера, воспроизводящая ряд одноименных величин различного размера, называется многозначной. Этот ряд может быть непрерывным или дискретным. Наиболее распространенными многозначными мерами являются миллиметровая линейка, вариометр индуктивности, конденсатор переменной емкости.
В качестве многозначной меры может быть использован набор мер - специально подобранный комплект мер, применяемых не только по отдельности, но и в различных сочетаниях с целью воспроизведения ряда одноименных величин различного размера; например набор гирь, набор образцовых конденсаторов и т. д.
Магазин мер - это набор мер, конструктивно объединенных в одно целое. Магазин мер имеет коммутирующее устройство для получения требуемого значения воспроизводимой величины, например магазин активных сопротивлений как набор резисторов.
При изготовлении наборов или магазинов мер к выбору ряда значений предъявляют особые требования. При этом стремятся наиболее рационально, используя наименьшее число мер, обеспечить возможность получения числа сочетаний. Например, набор гирь строится по ряду 1; 2; 2; 5 (в каждом десятичном числовом разряде), что дает возможность воспроизвести все значения от 1 до 10. Такой ряд признан более рациональным, чем ряд 1; 2; 3; 4, содержащий гири четырех размеров вместо трех. Это имеет большее значение при массовом производстве. Кроме того, гири 2 и 3, а особенно 3 и 4 не очень заметно отличаются по размерам, что усложняет пользование ими.
К наборам плоскопараллельных концевых мер длины предъявляется другое требование: любое значение длины (в заданных пределах) должно воспроизводиться с помощью не более чем четырех-пяти мер. Так, набор из 87 концевых мер от 0,5 до 100 мм позволяет воспроизводить длину от 0,5 до 340 мм с интервалами 0,005; 0,01 и 0,1 мм, применяя не более четырех концевых мер. Меры применяются как самостоятельные средства, так и в качестве элементов других средств измерений (приборов, преобразователей).
-
Измерительные преобразователи
Согласно ГОСТ 16263 - 70 измерительный преобразователь - это средство измерений, предназначенное для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и (или) хранения, но не поддающейся непосредственному восприятию наблюдателем. Принцип их действия основан на различных физических явлениях. Измерительные преобразователи преобразуют любые физические величины х (электрические, неэлектрические, магнитные) в выходной электрический сигнал Y = f(х).
Измерительные преобразователи являются составными частями измерительных приборов, установок и систем. Измерительные преобразователи можно классифицировать по характеру входной и выходной величин, месту в измерительной цепи, физическим явлениям, положенным в их принцип действия, и другим признакам (рис. 3.3).
Физические величины могут быть непрерывными по значению и квантованными (они представляются обычно кодовыми сигналами). Если входная и выходная величины измерительного преобразователя – непрерывные величины, такой преобразователь называют – аналоговым. Измерительный преобразователи одного кодового сигнала в другой получили название кодовых. Преобразователи аналог-код превращают непрерывную величину в кодовый сигнал, а преобразователи код-аналог - кодовый сигнал в сигнал, непрерывный по значению (например, преобразователь двоичного числа в постоянное напряжение).
  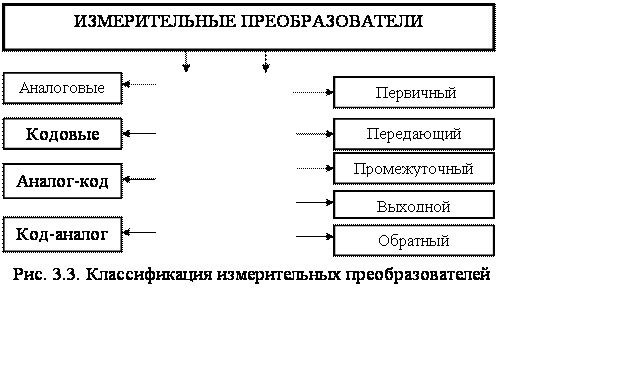
По месту, занимаемому в измерительной цепи, средства измерения, преобразователи подразделяются на первичные, передающие, промежуточные, выходные и обратные.
Первичный преобразователь — это преобразователь, к которому подведена измеряемая величина. Для первичных преобразователей характерно то, что на них воздействует непосредственно измеряемая величина. Физическая величина, в которую преобразует измеряемую величину первичный преобразователь, может быть подведена к измерительному механизму, может быть подана на другой преобразователь или использована, например, для целей телеизмерений.
Примером первичного преобразователя может служить термопара в цепи термоэлектрического термометра.
Конструктивно обособленный первичный измерительный преобразователь, от которого поступают сигналы измерительной информации, называется датчиком [3].
Датчик может быть вынесен на значительное расстояние от средства измерений, принимающего его сигналы. Например, датчики запущенного метеорологического радиозонда передают измерительную информацию о температуре, давлении, влажности и других параметрах атмосферы; тензопреобразователь, наклеенный на упругий элемент и воспринимающий его деформацию, также является датчиком [8].
Передающий преобразователь - измерительный преобразователь, служащий для дистанционной передачи измерительной информации. Для этих преобразователей характерно назначение величины, образуемой на его «выходе». Очевидно, что преобразователь может одновременно выполнять функции первичного и передающего.
Промежуточный преобразователь — преобразователь, занимающий в измерительной цепи место после первичного.
Выходной преобразователь – преобразователь, стоящий последним в измерительной цепи. Он снабжается отсчетным или регистрирующим устройством, фиксирующим значение измеряемой величины.
Измерительные приборы сравнения (см. п. 3.4) имеют две цепи – прямого преобразования, начиная от входной величины, и обратного преобразования – к входной величине. Измерительные преобразователи, стоящие в цепи обратного преобразования, получили название обратных.
Для изменения в определенное число раз значения одной из величин, действующих в измерительной цепи, без изменения ее физической природы используют масштабные преобразователи: делители напряжения, измерительные трансформаторы тока, измерительные усилители и т. п.
Полезно также все измерительные преобразователи разделить на две группы: генераторные (энергетические) и параметрические. Первые характеризуются тем, что для осуществления преобразования не требуется постороннего источника энергии. Измерительный преобразователь её вырабатывает сам за счет воздействия преобразуемой величины. Параметрические же преобразователи должны быть возбуждены от постороннего источника энергии. Например, преобразователь в виде термопары для измерения температуры сам вырабатывает электрическую энергию, а термометр сопротивления (нагреваемая проволока) может осуществлять преобразование температуры в сопротивление только будучи нагретым источником электрического тока.
Измерительные преобразователи могут быть встроены в корпус прибора и вместе с другими его устройствами образовать единую конструкцию. В этом случае метрологические характеристики нормируются для измерительного прибора в целом. В тех случаях, когда измерительные преобразователи (один или несколько) являются конструктивно обособленными элементами, метрологические характеристики нормируются на эти элементы. Это очень важно при построении измерительных средств на базе блочно-модульного принципа, при построении измерительных установок и систем, которые могут включать десятки различных измерительных преобразователей.
Измерительные преобразователи бывают взаимозаменяемыми, ограниченно-взаимозаменяемыми и невзаимозаменяемыми или индивидуальными.
Взаимозаменяемые преобразователи могут без каких-либо ограничений заменять друг друга. При такой замене свойства прибора не должны измениться. Для того чтобы обеспечивалась такая взаимозаменяемость, нормируют ряд характеристик преобразователей. Для них устанавливают и стандартизуют рациональный ряд коэффициентов преобразования. Под коэффициентом преобразования понимается отношение значения величины на входе преобразователя к значению соответствующей ей величины на выходе.
Важные характеристики взаимозаменяемых преобразователей следующие: - значение входной и выходной величин каждой в отдельности. Так, напри-
мер, государственными стандартами устанавливаются следующие диапазоны изменения входных и выходных величин: сила постоянного электрического тока I= = 0…5 мA; 0…20 мA, постоянное напряжение U= = 0…10 В, переменное напряжение U~ = 0…2 В, частота электрических колебаний f = 1500…2500 Гц; 4000…8000 Гц [8]. Установление определенного ряда этих значений и обеспечивает широкую взаимозаменяемость преобразователей. Благодаря установлению таких рядов значительно сокращается количество разновидностей первичных преобразователей и вторичных устройств (конструктивно обособленная остальная часть элементов измерительной цепи).
- точность и постоянство коэффициента преобразования на всем диапазоне его работы.
Для большинства взаимозаменяемых преобразователей устанавливают классы точности. При выборе преобразователя стремятся к тому, чтобы его класс точности, если это возможно, был выше класса точности измерительного прибора, применяемого с преобразователем, иначе говоря, чтобы применение преобразователя как можно меньше снижало общую точность измерения данным прибором.
Требования, предъявляемые к взаимозаменяемым преобразователям, весьма высоки. В ряде случаев некоторые из них невыполнимы или выполнение их экономически нецелесообразно. Тогда их применяют ограниченно, причем ограничение накладывают на какое-либо одно требование.
Чаще всего взаимозаменяемые преобразователи используют только для измерительного прибора одного вида или типа, а иногда даже только одной его конструкции, о чем на преобразователе делается соответствующая надпись.
Применение индивидуальных (невзаимозаменяемых) преобразователей позволяет улучшить метрологические характеристики измерительного прибора и установки за счет специальных регулировок.
Измерительный прибор - средство измерения, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем.
Выработка измерительной информации может основываться на использовании различных физических принципов. Например, для измерения длины применяют механические, оптические, пневматические и электрические измерительные приборы.
Физический принцип, положенный в основу построения измерительного прибора, называют принципом действия прибора, который часто отражается в названии прибора, например, электродинамический ваттметр, термоэлектрический термометр.
Принципиально измерительный прибор состоит из ряда измерительных преобразователей, каналов связи, согласующих элементов, измерительного механизма, которые в совокупности образуют измерительную цепь прибора. Измерительная цепь осуществляет все преобразования сигнала измерительной информации.
Измерительная цепь начинается чувствительным элементом, являющимся составной частью первичного преобразователя. На элемент непосредственно воздействует измеряемая величина. Оканчивается цепь отсчетным устройством, с помощью которого наблюдатель определяет значение измеряемой величины, выраженное в принятых единицах измерения. Это значение называют показанием средства измерения, которое образуется от отсчета (отвлеченного числа), снятого при измерении с отсчетного устройства прибора. Переход от отсчета к показанию осуществляется умножением отсчета на цену деления шкалы, под которой понимается разность значений величины, соответствующих двум соседним отметкам шкалы.
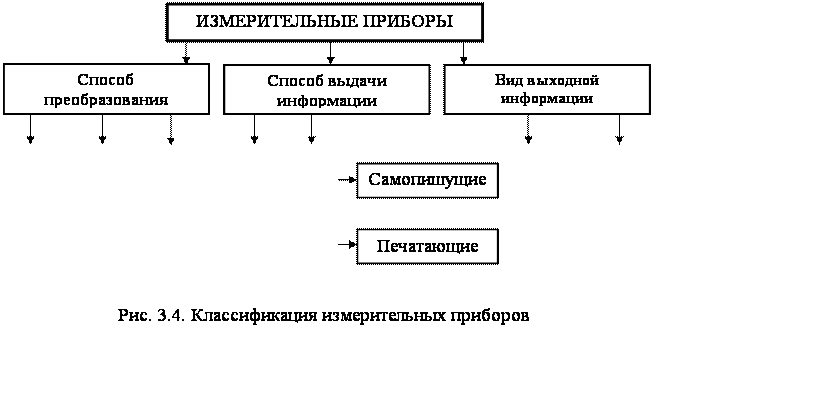
Измерительные приборы можно классифицировать по различным признакам: структуре преобразования; виду выходной информации; способу ее выдачи; роду измеряемой величины; условиям применения и т.д.
Классификация измерительных приборов с учетом этих признаков представлена на рис. 3.4.
Измерительные приборы по своей структуре представляют собой определенное сочетание измерительных преобразователей и устройства сравнения. Для условного изображения структуры прибора используется функциональная схема. По ней можно проследить все преобразования, которым
подвергается измеряемая величина в процессе работы прибора.
По структуре преобразования все измерительные приборы можно разделить на три вида: приборы прямого преобразования, приборы уравновешивающего преобразования и приборы смешанного преобразования.
Средства измерений прямого преобразования. Структурная схема прибора прямого преобразования показана на рас. 3.5, где ИП1, ИП2,…,ИПn -звенья; х, х1, х2,..., хn - информативные параметры сигналов.

Как видно из рис. 3.5, входной сигнал х последовательно претерпевает несколько преобразований и в итоге на выходе получается сигнал хn .
Для измерительного прибора сигнал xn получается в форме, доступной для непосредственного восприятия наблюдателем, например, в виде отклонения указателя отсчетного устройства. Для измерительного преобразователя сигнал хn получается в форме, удобной для передачи, дальнейшего преобразования, обработки и (или) хранения.
Примером электроизмерительного прибора, имеющего структурную схему прямого преобразования, может быть амперметр для измерения больших постоянных токов. В этом приборе измеряемый ток вначале с помощью шунта преобразуется в падение напряжения на шунте, затем в малый ток, который измеряется измерительным механизмом, т.е. преобразуется в отклонение указателя [11].
Структурная схема прибора прямого преобразования разомкнутая, в ней отсутствует общая обратная связь с выхода на вход. Если все измерительные преобразователи имеют линейную функцию преобразования (хi = ki×хi-1 ), то выходная величина связана с измеряемой величиной соотношением
хn = k1×k2¼kn×x = k×x , (3.1)
где k1 , k2 ,¼, kn - коэффициенты преобразования измерительных преобразователей.
Чувствительность (коэффициент преобразования) средства измерений, имеющего структурную схему прямого преобразования:
 k1×k2×k3¼kn . (3.2) k1×k2×k3¼kn . (3.2)
При нелинейной функции преобразования чувствительность и коэффициенты преобразования зависят от входного сигнала.
Мультипликативная погрешность возникает при изменении коэффициентов преобразования. С течением времени и под действием внешних факторов коэффициенты k1, k2, k3 ,¼, kn могут изменяться соответственно на Dk1, Dk2, Dk3 ,¼, Dkn. При достаточно малых изменениях этих коэффициентов можно пренебречь членами второго и большего порядков малости, тогда относительное изменение чувствительности
 . (3.3) . (3.3)
Изменение чувствительности приводит к изменению выходного сигнала на Dxn = (S + DS)×x -S×x=DS×x . Этому изменению выходного сигнала соответствует абсолютная погрешность измерения входной величины
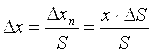 . (3.4) . (3.4)
Как видно из выражения (3.4), погрешность, вызванная изменением чувствительности, является мультипликативной. Относительная мультипликативная погрешность измерения dь = DS/S .
Аддитивная погрешность вызывается дрейфом «нуля» звеньев, наложением помех на полезный сигнал и т.д., приводящих к смещению графика характеристики преобразования i-гo звена на ±Dx0i; (как показано на рис. 3.6). Аддитивную погрешность можно найти, введя на структурной схеме после соответствующих звеньев дополнительные внешние сигналы Dx01 , Dx02, …, Dx0n , равные смещениям характеристик преобразования звеньев.
Для оценки влияния этих дополнительных сигналов пересчитаем (приведем) их ко входу структурной схемы. Результирующее действие всех дополнительных сигналов равно действию следующего дополнительного сигнала на входе: 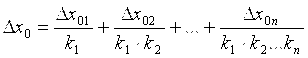 . (3.5) . (3.5)
 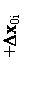 
Результирующая аддитивная погрешность равна Dx0. Таким образом, как следует из (3.3) и (3.5), в средствах измерений, имеющих структурную схему прямого преобразования, происходит суммирование погрешностей, вносимых отдельными звеньями, и это затрудняет изготовление средств измерений прямого преобразования с высокой точностью.
Средства измерений уравновешивающего преобразования. Структурная схема средства измерений уравновешивающего преобразования показана на рис. 3.7.
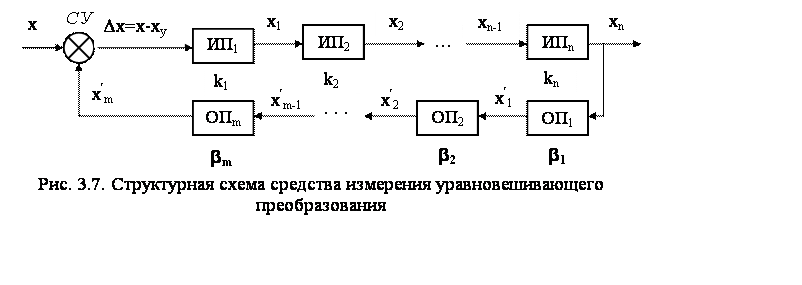
Структурная схема такого прибора содержит две цепи - цепь прямого преобразования и цепь обратного преобразования, т.е. в приборе имеется общая отрицательная обратная связь с выхода на вход.
Для цепи обратного преобразования (обратной связи)
x¢m = xn×b1×b2×…×bm = xn× b , (3.6)
где b - коэффициент преобразования цепи обратного преобразования; b1, b2, …, bm - коэффициенты преобразования звеньев обратной связи.
На входе цепи прямого преобразования в узле СУ происходит сравнение (компенсация) входного сигнала х и выходного сигнала цепи обратного преобразования х'm и при этом на выходе СУ получается разностный сигнал Dх = х—х'm .
При подаче на вход сигнала х выходной сигнал xn , а следовательно, и х'm , будут возрастать до тех пор, пока х и х'm не станут равны. При этом по значению xn можно судить об измеряемой величине х.
Средства измерений, имеющие такую структурную схему, могут работать как с полной, так и с неполной компенсацией.
При полной компенсации (астатическое преобразование) в установившемся режиме Dх = х—х'm =0 . (3.7)
Это возможно в тех устройствах, у которых в цепи прямого преобразования предусмотрено интегрирующее звено с характеристикой преобразования 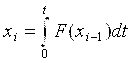 . Примером такого звена является электродвигатель, для которого угол поворота вала определяется приложенным напряжением и временем. . Примером такого звена является электродвигатель, для которого угол поворота вала определяется приложенным напряжением и временем.
В этом случае, учитывая (3.6) и (3.7), получим
xn = x/(b1×b2…bm) = x/b . (3.8)
Таким образом, в момент компенсации сигнал на выходе средства измерений пропорционален входному сигналу и не зависит от коэффициента преобразования цепи прямого преобразования.
Чувствительность (коэффициент преобразования)
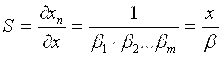 . (3.9) . (3.9)
Мультипликативная относительная погрешность, обусловленная нестабильностью коэффициентов преобразования звеньев, при достаточно малых изменениях этих коэффициентов
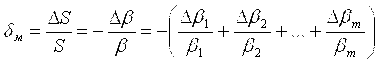 . (3.10) . (3.10)
Как видно из этого выражения, относительная мультипликативная погрешность обусловлена только относительным изменением коэффициента преобразования цепи обратного преобразования.
Аддитивная погрешность в средствах измерений с полной компенсацией практически обусловливается порогом чувствительности звеньев, расположенных до интегрирующего звена, и порогом чувствительности самого интегрирующего звена.
Под порогом чувствительности звена понимается то наименьшее изменение входного сигнала, которое способно вызвать появление сигнала на выходе звена. Порог чувствительности имеют, например, электродвигатели, часто применяемые в рассматриваемых устройствах. Для реальных звеньев график характеристики преобразования может иметь вид, как показано на рис.3.8, где ± Dх i-1 - порог чувствительности.
 Порог чувствительности средства измерений с полной компенсацией Порог чувствительности средства измерений с полной компенсацией 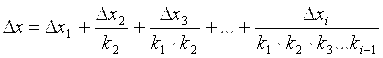 , (3.11) , (3.11)
где Dx1, Dx2 , … , Dxi-1 - пороги чувствительности
звеньев цепи прямого преобразования; Dxi - порог чувствительности интегрирующего звена.
При наличии порога чувствительности средства измерении состояние компенсации наступает при х - х'm =Dх. Таким образом, изменение входного сигнала в пределах ±Dx не вызывает изменения выходного сигнала, т.е. появляется абсолютная аддитивная погрешность, значение которой может быть в пределах ±Dx.
Из выражения (3.11) очевидно, что для уменьшения аддитивной погрешности, обусловленной порогом чувствительности звеньев, следует увеличивать коэффициенты преобразования k1 ,k2 , ..., ki-1. Предел увеличения этих коэффициентов обусловлен динамической устойчивостью средства измерений.
При неполной компенсации (статическое преобразование) в средствах измерений интегрирующего звена нет и обычно выполняется условие (3.6), а также
xn = k×Dx, (3.12)
где k=k1× k2 ... kn - коэффициент преобразования цепи прямого преобразования. В этом случае установившийся режим наступает при некоторой разности
Dх = х—х'm (3.13)
Зависимость между выходным и входным сигналами, находимая путем решения уравнений (3.6), (3.12) и (3.13),
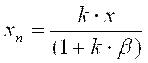 (3.14) (3.14)
Как видно из выражения (3.14), при установившемся режиме выходной сигнал пропорционален входному и зависит от коэффициентов цепи как обратного, так и прямого преобразования.
Если выполняется условие k×b » 1, то уравнение (3.14) переходит в (3.8) и при этом нестабильность коэффициента преобразования цепи прямого преобразования не влияет на работу устройства. Практически, чем выше k×b , тем меньше влияние k. Предел увеличения k×b обусловлен динамической устойчивостью средства измерений.
Чувствительность (коэффициент преобразования) средства измерений с неполной компенсацией
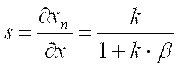 . (3.15) . (3.15)
Мультипликативная погрешность, обусловленная изменением коэффициентов преобразования звеньев при достаточно малых изменениях этих коэффициентов:
 , (3.16) , (3.16)
где dk = Dk/k; db = Db/b. Если k×b » 1, то dм » dk/k×b . Следовательно, при k×b » 1 (что обычно имеет место) составляющая, обусловленная изменением коэффициента b, целиком входит в результирующую погрешность, а составляющая, обусловленная изменением коэффициента k, входит в результирующую погрешность ослабленной в k×b раз. Нелинейность характеристики преобразования цепи прямого преобразования можно рассматривать как результат влияния изменения коэффициента преобразования k относительно некоторого начального значения при х=0. Полученные уравнения показывают, что нелинейность характеристики преобразования уменьшается действием отрицательной обратной связи в k×b раз.
Аддитивная погрешность может быть найдена путем введения в структурную схему дополнительных сигналов Dx01, Dx02,…, Dx0n, Dx¢01, Dx¢02,…, Dx¢0m , равных смещениям характеристик преобразования соответствующих звеньев.
Применяя методику, рассмотренную выше, получим абсолютную аддитивную погрешность, равную погрешности:
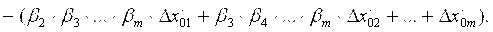 
Следует отметить, что средства измерений могут иметь комбинированные структурные схемы, когда часть цепи преобразования охвачена обратной связью.
Вид структурной схемы средства измерений влияет не только на рассмотренные характеристики (чувствительность, погрешность), но также на входные и выходные сопротивления, динамические свойства и др.
По виду выдаваемой информации все приборы делятся на аналоговые и цифровые. Аналоговым является измерительный прибор, показания которого являются непрерывной функцией измеряемой величины, например, стрелочный вольтметр. Цифровым называется измерительный прибор, автоматически вырабатывающий дискретные сигналы измерительной информации, показания которого представлены в цифровой форме, например, цифровой омметр.
По способу выдачи измерительной информации измерительные приборы делятся на показывающие и регистрирующие (см. рис. 3.4).
Показывающие приборы (рис. 3.9), если на них воздействует измеряемая величина, допускают только отсчитывание показаний. Указатель отсчетного

устройства перемещается относительно шкалы и наблюдается визуально. Шкала средства измерения - это часть отсчетного устройства, представ-ляющая собой совокупность отметок и проставленных у некоторых из них чисел отсчета или других символов, соответ-ствующих ряду последователь-ных значений измеряемой величины.
Шкалы с делениями постоянной длины и с постоянной ценой деления называются равномерными шкалами, а шкалы с делениями непостоянной длины - неравномерными.
Примерами показывающих приборов со шкалами могут служить следующие типы приборов: 1) электромеханические: М2027, М2042, ЭА2231; 2) электронные: В3-38, В2-25, В7-13 и др.

К показывающим измерительным приборам относят также приборы с цифровым отсчетом (рис.3.10). Их отсчетное устройство выдает показания в цифровой форме, показанное число соответствует значению измеряемой величины.
Измерительные приборы с цифровым отсчетом находят все большее распространение, поскольку они более производительны и удобны для наблюдателя. Примерами показывающих приборов с цифровым отсчетом могут служить следующие типы приборов: В2-37, Щ4310, Ч3-34, В7-22, В7-21 и др.
Регистрирующие измерительные приборы (рис.3.11) содержат механизм регистрации показаний. Регистрирующий прибор, в котором предусмотрена запись показаний в форме диаграммы, называют самопишущим прибором.

Диаграмма представляет собой изображение измерений измеряемой величины в зависимости от изменений другой переменной величины. Запись производится на бумаге в виде движущейся ленты или диска, наложенного на барабан. Способы записи, применяемые в настоящее время, весьма разнообразны. Наиболее распространены запись чернилами посред-ством пера той или иной конструкции и печатание точек через цветные ленты, пропитанные краской. Существуют и другие способы записи: тонкой струйкой чернил, электрической искрой на метал-лизированной бумаге, нагретым стержнем на бумаге с восковым слоем и т. д.
К регистрирующим следует отнести измерительные приборы с печатающими механизмами, дающими показание в виде чисел, отпечатанных на бумажной ленте. Примерами регистрирующих приборов могут служить следующие типы приборов: Н30, Н32, Н310, Н3140 и др.
По роду измеряемой величины приборам присвоены наименования в зависимости от названия единицы этой величины (в том числе кратных и дольных единиц), для измерения которой они предназначены: амперметры, микроамперметры - для измерения тока; веберметры, милливеберметры - для измерения магнитной индукции и т.д.
-
Измерительные установки и системы
Измерительная установка - это совокупность функционально объединенных средств измерений (мер, измерительных приборов, измерительных преобразователей) и вспомогательных устройств, предназначенных для выработки сигналов измерительной информации в форме, удобной для непосредственного восприятия наблюдателя и расположенных в одном месте. В качестве примера можно привести измерительные установки для измерений удельного сопротивления электротехнических материалов, для поверки счетчиков электрической энергии и др.
Измерительные установки в большинстве случаев обладают большей или меньшей универсальностью как в отношении номенклатуры измеряемых величин, так и в отношении диапазонов измерения. Иногда установки более узкого назначения называют измерительными машинами. К измерительным машинам относятся силоизмерительные машины и машины для измерения больших длин.
Измерительная система также представляет собой совокупность средств измерений и вспомогательных устройств, но предназначенных для выработки сигналов измерительной информации в форме, удобной для автоматической обработки, передачи и использования в автоматических системах управления.
Средства измерений могут находиться в разных местах, а передача измерительной информации осуществляться по специальным каналам связи. Измерительные системы широко используются для автоматизации технологических процессов в различных отраслях промышленности, сельского хозяйства и энергетики.
С развитием вычислительной техники, совершенствованием измерительных систем открываются возможности перехода на автоматизированную технологию во многих отраслях народного хозяйства. В этом случае управление технологическим процессом берет на себя вычислительно-измерительный комплекс, включающий широко разветвленную измерительную систему, функционально связанную с ЭВМ.
Таким образом, измерительная информация, вырабатываемая измерительной системой, является основой для автоматизации технологических процессов [4].
-
Метрологические характеристики средств измерений
Измерительная техника обладает большим арсеналом разнообразных средств измерений, предназначенных для решения различных измерительных задач. Все средства измерений можно характеризовать некоторыми общими свойствами - метрологическими характеристиками.
Метрологическими характеристиками средств измерений называются такие характеристики их свойств, которые оказывают влияние на результаты и погрешности измерений и предназначены для оценки технического уровня и качества средств измерений, для определения результатов измерений и расчетной оценки характеристик инструментальной и методических составляющих погрешности измерений [6]. Комплекс метрологических характеристик позволяет оценить метрологические (измерительные) возможности конкретного средства измерений, а также легко сопоставлять между собой различные разновидности этих средств. Метрологические характеристики средств измерений установлены ГОСТ 8.009-84. Рассмотрим основные из них.
Измеряемая, преобразуемая или воспроизводимая (для мер) величина. Этот параметр характеризует назначение средства измерений для измерения той или иной физической величины (напряжение, масса, температура, ускорение, ток и т.д.). Эта величина обычно наносится на средство измерений или указывается в технической документации.
Предел и диапазон измерений. Очень важной характеристикой любого средства измерения, определяющей в первую очередь пригодность его для тех целей, для которых оно предназначено, являются пределы измерения, т.е. наименьшее и наибольшее значения измеряемой величины, могущие быть измеренными данным средством измерений.
Диапазон измерений – область значений величины, в пределах которой нормированы допускаемые пределы погрешности средства измерений.
Значения величины, ограничивающие диапазон измерений снизу и сверху (слева и справа), называют соответственно «нижним пределом измерений» или «верхним пределом измерений» [3].
 Нижний предел измерения реально не бывает равным нулю, так как он ограничивается обычно порогом чувствительности, помехами или погрешностями измерений. Поэтому для многих измерительных приборов, на шкале которых имеется отметка « 0 », нижний предел измерения в действительности не равен нулю. Нижний предел измерения реально не бывает равным нулю, так как он ограничивается обычно порогом чувствительности, помехами или погрешностями измерений. Поэтому для многих измерительных приборов, на шкале которых имеется отметка « 0 », нижний предел измерения в действительности не равен нулю.
Различают полный и рабочий диапазоны измерения измеряемой величины (рис. 3.12).
Диапазон, в котором относительная погрешность не превышает 100 %, называ-ется полным диапазоном. Полный диапазон огра- ничивается снизу порогом чувствительности Dпор., а сверху – конечным значе- нием Xk, т.е. Хп = Dпор … Xk или Дп = Xk/Dпор. Под порогом чувствительности понимается такое значение измеряемой величины, когда Х = Dпор и относительная погрешность её измерения d = 100 % .
Диапазон, в котором относительная погрешность не превышает некоторого заранее заданного значения dз , называется рабочим диапазоном изменения измеряемой величины. Рабочий диапазон ограничивается снизу значением Х=Хз , при котором d = dз , а сверху – конечным значением Xk , т.е. Хр = Хз … Хk или Др = Хk/ Хз. Рабочий диапазон всегда представляет часть полного диапазона.
Во многих измерительных приборах имеются специальные устройства, позволяющие изменить диапазон измерения иногда в очень широких пределах. В этих случаях следует говорить об общем диапазоне измерения, охватываемом измерительным прибором, и об отдельных диапазонах, которые часто называют неудачно «поддиапазоны». Например, общий диапазон измерения 0 - 100 делится на диапазоны 0 - 0,1; 0 - 1; 0 - 10; 0 - 100 или общий диапазон 0 - 5 делится на диапазоны 0 - 1; 1 - 2; 2 - 3; 3 - 4; 4 - 5.
Для преобразователей верхним и нижним пределами преобразования следует считать соответственно наибольшее и наименьшее значения входной и выходной величины, в пределах которых нормировано уравнение преобразования или коэффициент преобразования.
Для однозначных мер вместо диапазона значений воспроизводимых величин используют понятие номинальное значение меры, т.е. значение величины, указанное на мере или приписанное ей. Часто измерительный прибор имеет участки, на которых его погрешность не нормирована (обычно в начале и конце шкалы). В таком случае для прибора указывается еще и диапазон показаний - область значений шкалы, ограниченная конечным и начальным значениями шкалы. Диапазон показаний всегда шире диапазона измерений.
Градуировочная характеристика средства измерений (уравнение преобразования) представляет зависимость между значениями величин на выходе ( Y ) и входе ( X ) средства измерений. Уравнение преобразования Y = f(X) может быть представлено в виде формулы, таблицы или графика.
Градуировочная характеристика средства измерений может быть линейной или нелинейной. Чаще всего стремятся иметь линейную зависимость, т.е. Y = k×X . Нелинейность уравнения преобразования стараются скомпенсировать добавлением измерительного преобразователя с такой градуировочной характеристикой, чтобы совместная характеристика преобразования стала линейной. Линейная градуировочная характеристика может как проходить через начало координат (Х= 0; Y= 0), так и иметь смещение по оси Х или Y (например, Y = 0 при X = X0 , средство измерений с подавленным нулем, смещенной шкалой).
Для средств измерений нормируется номинальная статическая градуировочная характеристика. Она приписывается средству измерений на основе анализа совокупности таких средств. Реальная градуировочная характеристика конкретного образца средства измерении может несколько отличаться от номинальной.
Чувствительность измерительного прибора (коэффициент преобразования измерительного преобразователя) определяется как отношение приращения выходного сигнала DY на выходе измерительного прибора (преобразователя) к вызвавшему это приращение изменению входного сигнала DХ (входного сигнала преобразователя). В общем случае чувствительность определяется как
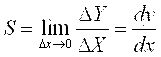
и называется абсолютной чувствительностью. Эта величина является размерной и зависит от единиц, в которых выражаются X и Y .Для линейной градуировочной характеристики чувствительность S = const, для нелинейных характеристик чувствительность является переменной величиной, различной для разных значений Х .
В практике пользуются относительной чувствительностью
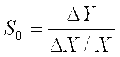 , ,
где DX/X - относительное изменение входной величины, выражаемое чаще всего в процентах. Относительная чувствительность S0 имеет размерность выходной величины на 1% изменения входной величины.
Применяют также выражение относительной чувствительности в виде
 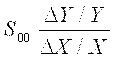 , ,
выражая числитель и знаменатель чаще всего в процентах (например, 1 % изменения вызывает изменение Y на n %). Отметим, что S00 - величина безразмерная.
Для стрелочных приборов S = a /x. Поэтому измеряемая величина 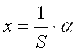 , где a - показание прибора; 1/S – постоянная прибора или цена деления. , где a - показание прибора; 1/S – постоянная прибора или цена деления.
Для измерительных приборов и мер с переменным значением часто вместо чувствительности указывают цену деления шкалы. Цена деления представляет собой разность значений величины, соответствующих двум соседним отметкам шкалы. Цена деления есть величина, обратная чувствительности. Она имеет размерность измеряемой величины. В приборах с линейной градуировочной характеристикой цена деления постоянна в диапазоне измерений и носит название - постоянная прибора. Для получения значения величины в соответствующих единицах надо умножить отсчет в делениях на постоянную прибора.
Порог чувствительности средства измерений определяется как изменение измеряемой величины, вызывающее наименьшее изменение выходной величины, которое может быть обнаружено с помощью данного средства измерений без каких-либо дополнительных устройств [2]. Введение этого параметра вызвано тем, что не всякое малое изменение измеряемой величины вызывает изменение результата измерения, а только лишь большее некоторой пороговой величины. Порог чувствительности равен абсолютной погрешности средства измерений, т.е. Dпор. = DХ.
В электромеханических измерительных преобразователях (измеряемая величина - угол) порог чувствительности не равен нулю вследствие трения подвижной части, а в цифровых измерительных приборах показание изменяется, если изменение входной величины больше шага квантования. Обычно порог чувствительности выражается в единицах входной величины.
Вариация выходного сигнала (показаний) средства измерений есть средняя разность между значениями выходного сигнала (показаниями) средства измерений, соответствующими данной точке диапазона измерения, при двух направлениях медленного многократного измерения входного сигнала в процессе подхода к данной точке диапазона измерения [3]. Вариация определяется по значениям выходного сигнала при подходе к одному и тому же значению входного сигнала сначала со стороны больших, а затем - меньших значений. В отличие от чувствительности вариация характеризуется изменением не входного, а выходного сигнала.
Точность средства измерений есть качество средства измерений, отражающее близость нулю его погрешностей. Чем меньшие погрешности имеет средство измерений, тем оно считается более точным. Для всех средств измерений указываются метрологические характеристики погрешностей. Они включают в себя: характеристики систематической составляющей погрешности, случайной составляющей, а также вариации выходного сигнала. В соответствии с ГОСТ 8.009 - 84 нормирование характеристик погрешностей производится на основе методов математической статистики. Методы количественного выражения характеристик погрешностей будут рассмотрены в разделе 4.
Потребляемая мощность. Входное и выходное сопротивления.
Измеряемый объект и средство измерений связаны и взаимодействуют между собой. Такое взаимодействие необходимо для проведения измерения.
Для приведения в действие первичного измерительного преобразователя необходима энергия, которая потребляется от объекта измерения. Естественно, эта энергия должна быть небольшой, чтобы измерительный прибор не вносил заметного искажения в измеряемый процесс. Сравните между собой измерение ртутным термометром температуры моря и жидкости в пробирке. Во втором случае термометр может существенно нагреть или охладить жидкость в пробирке. Поскольку мощность, потребляемая входной цепью прибора, конечна, ее значение является важным показателем средства измерения.
У средств измерений электрических величин потребляемая мощность определяется входным сопротивлением прибора. Для приборов, реагирующих на напряжение (включаемых параллельно участку цепи), входное сопротивление должно быть большим, тогда входная мощность Р = U2/R будет невелика. У приборов, чувствительных к току (включаемых последовательно в электрическую цепь), входное сопротивление, наоборот, должно быть минимальным (по крайней мере, намного меньшим, чем сопротивление участка цепи).
Понятие входного сопротивления применяется не только к измерению электрических величин, но и к измерению механических, тепловых и другого рода величин. В связи с этим нашло применение более общее понятие: обобщенное входное сопротивление, определяемое как отношение обобщенной силы к обобщенной скорости. Например, под механическим сопротивлением понимают отношение силы к вызванной ею скорости равномерного движения. Однако не для всех видов энергии понятие сопротивления соответствует общему определению.
Входное сопротивление является важным параметром средства измерений. Оно показывает степень приспособленности данного средства к измерениям в маломощных измерительных цепях. Если мощность, потребляемая входной цепью прибора, одного порядка с мощностью входного сигнала, приходится вводить поправки или обеспечивать согласование прибора с источником измерительного сигнала.
Выходное сопротивление измерительного преобразователя характеризует реакцию его выходного сигнала на подключение к его выходу фиксированной нагрузки. Преобразователь с выходной стороны бывает нагружен входным сопротивлением последующего измерительного преобразователя. Для наиболее эффективного использования преобразователей необходимо согласование выходного сопротивления данного преобразователя с входным сопротивлением последующего преобразователя. Чем меньше выходное сопротивление предшествующего преобразователя по отношению к входному сопротивлению следующего преобразователя, тем меньше потребляемая последующим преобразователем мощность и тем меньше взаимная зависимость характеристик преобразователей.
Динамические характеристики средств измерений возникают при динамическом режиме его работы. Динамический режим работы средства измерений - это такой режим, при котором средство измерений воспринимает изменение входной величины и размеры измеряемой величины изменяются во времени.
Динамические характеристики средства измерений описывают инерционные свойства средств измерений и определяют зависимость выходного сигнала средств измерений от меняющихся во времени величин: входного сигнала, нагрузки, влияющих величин [6].
Для описания поведения большинства средств измерений в динамическом режиме работы с достаточной степенью приближения можно использовать линейное дифференциальное уравнение с постоянными коэффициентами [11]:
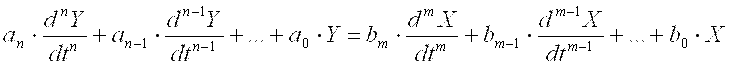 , ,
где an … a0 и bn …b0 - постоянные коэффициенты; Y и Х - мгновенные значения информативного параметра изменения выходной и измеряемой величин.
Таким образом, динамические характеристики определяют характер переходного процесса, протекающего в средстве измерений.
Средства измерения при любом изменении входной величины можно характеризовать операторной чувствительностью, определяемой как отношение операторного изображения информативного параметра изменения выходной величины Y(p) к операторному изображению измеряемой величины X(p):
 , ,
где 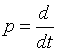 - оператор Лапласа. - оператор Лапласа.
Для измерительных преобразователей динамические характеристики обычно выражают в виде переходных или амплитудно- и фазочастотных характеристик.
При ступенчатом изменении входной величины x = x0 = const средства измерения описываются переходной характеристикой
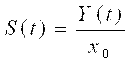 . .
В случае гармонического изменения входной величины используется комплексная чувствительность
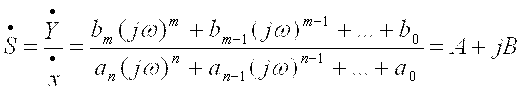 , ,
где A и B – вещественная и мнимая части комплексной чувствительности.
Модуль комплексной чувствительности называется амплитудно-частотной характеристикой:
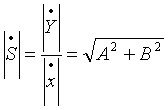 , ,
а аргумент – фазочастотной характеристикой:
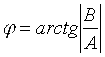 . .
Для измерительных приборов обычно указывается время установления показания: промежуток времени с момента начала измерения до момента установления показаний (т.е. когда переходный процесс закончился). Величина, обратная времени измерения, получила название быстродействия средства измерения. Быстродействие выражается числом, равным максимальному числу измерений с помощью данного прибора в секунду. Время измерения стрелочных измерительных приборов составляет обычно 4 с, а быстродействие цифровых измерительных приборов может достигать величин 106 измерений в секунду.
Высокое быстродействие дает возможность измерять мгновенные значения быстроменяющихся величин, а также дает возможность повышать точность измерений введением дополнительных вычислительных устройств для обработ-ки большого числа единичных измерений.
Условия применения средств измерений. При использовании средств измерений в реальных условиях необходимо учитывать характеристики среды, в которой это средство измерений находится при эксплуатации. Изменение внешних условий приводит к изменению метрологических характеристик, т.е. к увеличению погрешностей измерения. Величины, которые влияют на метрологические характеристики, помимо измеряемой величины называют влияющими величинами. Влияющими величинами могут быть: температура, влажность, атмосферное давление, напряжение источника питания, напряженность внешних магнитных и электрических полей, вибрации и ускорения и т.д. Кроме того, влияющими величинами считаются те параметры входного сигнала, изменения которых не несут информации об измеряемой величине, но влияют на результаты измерений. Например, показания электронного вольтметра зависят не только от величины переменного напряжения, но и его частоты.
В стандартах или технических условиях (ТУ) на средства измерений обычно указывают области значений влияющих величин, обеспечивающих работоспособность и сохранность средств измерений. Так, например, под лабораторными условиями эксплуатации обычно понимаются такие, когда температура окружающего воздуха лежит в пределах +(15-25) 0С, относительная влажность воздуха от 45 до 75 %, атмосферное давление
(860-1060) 102 Па.
Различают нормальные условия применения средств измерений, рабочие условия применения и предельные условия хранения и транспортирования.
При работе средства измерений в нормальных условиях воздействием влияющих величин на результаты измерений можно пренебречь. Метрологические характеристики погрешностей и динамические характеристики средств измерений обычно нормируются для нормальных условий эксплуатации. Считается, что погрешность в этих условиях определяются только конструкцией прибора. Часто такую погрешность называют основной погрешностью.
Обычно средства измерений продолжают нормально выполнять функции в более широкой области значений влияющих величин. В этом случае для средств измерений указываются рабочие условия эксплуатации. Метрологические характеристики средств измерений в рабочих условиях могут существенно изменяться под воздействием влияющих величин. Для оценки этого изменения могут применяться функции влияния.
Функция влияний представляет собой зависимость изменений метрологической характеристики средства измерений от изменений влияющих величин в пределах рабочих условий эксплуатации. По ГОСТ 8.009 - 84 функции влияния должны нормироваться отдельно для каждого влияющего фактора и могут выражаться в виде формул, таблиц или графиков. Допускается также вместо функции влияния характеризовать средства измерений наибольшим допустимым изменением метрологических характеристик в пределах рабочих условий.
С помощью функций влияния можно оценить погрешность средства измерений при работе его в тех или иных конкретных условиях. Погрешность, обусловленная воздействием влияющих величин, часто называется дополнительной погрешностью средства измерений.
Отметим, что функции влияния не нашли пока широкого применения в измерительной технике, так как для их достоверной оценки необходимо большое число испытаний приборов. Кроме того, суммарная погрешность средства измерений от совокупности внешних факторов во многих случаях не является суммой погрешностей от каждого фактора в отдельности.
Предельные условия хранения и транспортирования задаются областью значений влияющих величин, при которых возможно хранение и перевозка средств измерений в нерабочем состоянии. Однако после возвращения средств измерений в рабочие условия эксплуатации их метрологические характеристики не должны измениться. Предельные условия характеризуются наиболее широкими областями значений влияющих величин, выход влияющих величин за предельные условия приводит обычно к поломке средства измерений.
Кроме метрологических характеристик при эксплуатации средств измерения важно знать и неметрологические характеристики: показатели надежности, электрическую прочность, сопротивление изоляции, устойчивость к климатическим и механическим воздействиям, время установления рабочего режима, экономичность и др. [11]. Рассмотрим некоторые из них.
Надежность средств измерений. Под надежностью средств измерений понимают его способность сохранять эксплуатационные параметры в установленных пределах в течение заданного времени.
Одной из важных количественных характеристик надежности средства измерений является вероятность безотказной работы. Так, например, если обозначить через t время от момента включения средства измерений в работу до момента, когда по каким-либо причинам оно вышло из строя или уже не отвечает своим метрологическим параметрам, а через t - рассматриваемый промежуток времени (здесь t - случайная величина), то
p(t) = p(t ³ t),
где p(t) – вероятность того, что данное средство измерений будет работоспособно в рассматриваемый промежуток времени.
В настоящее время в технических условиях на любое средство измерения указываются требования к характеристикам надежности. Например, за t=1000 ч величина p(t) должна быть не менее 0,85, т.е. p(t) ³ 0,85.
Помимо вероятности безотказной работы по Государственной системе приборов (ГСП) существуют и другие критерии надежности средств измерения, такие как интенсивность отказов, среднее время безотказной работы, время восстановления [7]. Оценка надежности производится в процессе разработки средства измерений (ГОСТ 22261 – 82).
Экономичность средств измерений – простота конструкций в обращении и оправданная экономическая стоимость.
-
Погрешности средств измерений
Составляющая погрешности измерений, обусловленная свойствами применяемых средств измерений (далее СИ), называется инструментальной погрешностью измерения. Эта погрешность является важнейшей метрологической характеристикой СИ и определяет, насколько действительные свойства средств измерений близки к номинальным.
Согласно ГОСТ 8.009—84, следует различать четыре составляющие погрешности средств измерений: основную; дополнительную; обусловленную взаимодействием средств и объекта измерений; динамическую.
Основная погрешность. Она обусловлена неидеальностью собственных свойств средств измерений и показывает отличие действительной функции преобразования средств измерений в нормальных условиях от номинальной функции преобразования.
По способу числового выражения основной погрешности различают абсолютную, относительную и приведенную погрешности.
Абсолютная погрешность измерительного прибора - разность между показанием прибора Хп и истинным значением Хи измеряемой величины:
DХ = Хп – Хи.
Абсолютная погрешность, взятая с обратным знаком, называется поправкой:
П = - DХ .
Под абсолютной погрешностью меры DХ понимается разность между номинальным значением меры Хн и действительным значением воспроизводимой ею величины Хд :
DХ = Хн—Хд .
Относительная погрешность измерительного прибора в процентах - отношение абсолютной погрешности к истинному значению измеряемой величины:
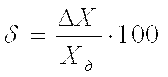 . .
Относительная погрешность обычно существенно изменяется вдоль шкалы аналогового прибора, с уменьшением значений измеряемой величины -увеличивается.
Если диапазон измерения прибора охватывает и нулевое значение измеряемой величины, то относительная погрешность обращается в бесконечность в соответствующей ему точке шкалы. В этом случае пользуются понятием приведенной погрешности.
Приведенная погрешность измерительного прибора в процентах - отношение абсолютной погрешности к нормирующему значению ХN :
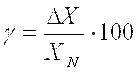 . .
За нормирующее значение принимается значение, характерное для данного вида измерительного прибора. Это может быть, например, верхний предел измерений, длина шкалы и т.д. Например. приведенная погрешность вольтметра с верхним пределом измерения 150 В при показании его 100,0 В и действительном значении измеряемого напряжения 100,6 В равна 0,4 % (нормирующее значение в данном случае равно 150 В). Точность ряда средств измерений с различными диапазонами измерений может сопоставляться только по их приведенным погрешностям.
Основная погрешность прибора - погрешность при нормальных условиях использования прибора. Нормальные условия эксплуатации зависят от назначения прибора и его метрологических характеристик. Для основной массы приборов, используемых в промышленности, нормальными условиями эксплуатации СИ считаются : температура окружающего воздуха (20±5) °С; относительная влажность 30-80 %; атмосферное давление 630-795 мм рт. ст.; напряжение питающей сети (220+4,4) В; частота питающей сети (50±0,5) Гц.
По характеру влияния на функцию преобразования ее можно представить в виде аддитивной и мультипликативной составляющих.
Аддитивная погрешность а не зависит от чувствительности прибора и является постоянной для всех значений входной величины в пределах диапазона измерений (прямая 3, рис. 3.13) и поэтому её называют погрешностью нуля.
Мультипликативная погрешность b×х зависит от чувствительности прибора и изменяется пропорционально текущему значению входной величины (прямая 2, рис. 3.13) и поэтом её называют погрешностью чувствительности.
Суммарная абсолютная погрешность выражается уравнением
D = a + b×x,
т.е. аддитивная и мультипликативная погрешности присутствуют одновременно (прямая 1, рис. 3.13).
 К аддитивной погрешности прибора можно отнести погрешность, вызванную трением в опорах электроизмерительных приборов, которая не зависит от значения входного сигнала, а также помехи, шумы, погрешность дискретности (квантования) в цифровых приборах. Если прибору присуща только аддитивная погрешность или она существенно превышает другие составляющие, то целесообразно нормировать абсолютную погрешность. К аддитивной погрешности прибора можно отнести погрешность, вызванную трением в опорах электроизмерительных приборов, которая не зависит от значения входного сигнала, а также помехи, шумы, погрешность дискретности (квантования) в цифровых приборах. Если прибору присуща только аддитивная погрешность или она существенно превышает другие составляющие, то целесообразно нормировать абсолютную погрешность.
К мультипликативной погрешности можно отнести погрешности изготовления добавочного резистора в вольтметре или шунта в амперметре, погрешности коэффициента деления делителя и т. д. Мультипликативная составляющая абсолютной погрешности увеличивается с увеличением измеряемой величины, а так как относительная погрешность остается постоянной, то в этом случае целесообразно нормировать погрешность прибора в виде относительной погрешности.
Аддитивная и мультипликативная погрешности могут иметь как систематический, так и случайный характер.
Систематическая погрешность средства измерений - составляющая погрешности средства измерения, остающаяся постоянной или закономерно изменяющаяся при многократных измерениях одной и той же величины. К постоянным систематическим погрешностям относят погрешности градуировки шкалы аналоговых приборов; калибровки цифровых приборов; погрешности, обусловленные неточностью подгонки резисторов, температурными изменениями параметров элементов в приборах и т.д. К переменным систематическим погрешностям относят погрешности, обусловленные нестабильностью напряжения источника питания, влиянием электромагнитных полей и других величин.
Случайная погрешность средства измерений - составляющая погрешности средства измерений, изменяющаяся случайным образом. Случайные погрешности могут возникнуть из-за нестабильности переходного сопротивления в контактах коммутирующих устройств, трения в опорах подвижной части приборов и т. д.
К случайным погрешностям относятся также погрешности от гистерезиса -вариации показаний выходного сигнала средства измерения.
Таким образом, при определении основной погрешности абсолютная погрешность может быть представлена ее составляющими - систематической и случайной.
Дополнительная погрешность. Дополнительная погрешность обусловлена реакцией средства измерений на отклонение условий эксплуатации от нормальных. В эксплуатационных условиях при установке прибора, например, на самолет, ему приходится работать при изменении температуры от - 60 до +60 °С, давления - от 1000 до 100 ГПа, напряжения питания - на ±20 %, коэффициента гармоник - от 1 до 10 % и т. д. Это приведет к появлению погрешностей, естественно, больших, чем в нормальных (лабораторных) условиях или условиях поверки.
Если статическая характеристика преобразования средства измерений имеет вид y =F(x, x1, x2,…, xn), где y - выходная величина; х — входная величина; x1, x2,…, xn - влияющие величины, то изменение выходной величины Dy определяется не только изменением измеряемой величины Dх, но и изменениями влияющих величин Dx1, Dx2,…, Dxn. В этом случае
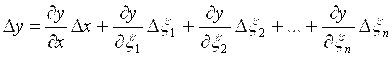 . .
В этом выражении второй и последующие члены правой части являются составляющими погрешности. Если изменения влияющих величин находятся в пределах нормальных условий, то все указанные составляющие входят в состав основной погрешности. При отклонении влияющих величин за пределы нормальных условий приращения указанных составляющих образуют дополнительные погрешности от изменения величин x1, x2,…, xn. Функции
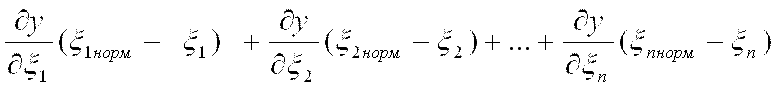
называют функциями влияния, в которых x1 норм , x2 норм , … xn норм - нормальные значения влияющих величин; x1, x2,…, xn - влияющие величины, для которых определяют дополнительные погрешности. Производные 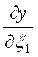 , , 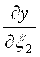 , … , , … , 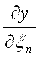 называют коэффициентами влияния. называют коэффициентами влияния.
Дополнительные погрешности нормируются указанием коэффициентов влияния изменения отдельных влияющих величин на изменение показаний в виде: yq , % / 10 К - коэффициент влияния от изменения температуры на 10 К; yU, % / (10 % DU/U) – коэффициент влияния от изменения напряжения питания на 10 % и т. д. Хотя фактически эти функции влияния влияющих факторов, как правило, нелинейны, для простоты вычислений их приближенно считают линейными и возникающие дополнительные погрешности определяют как gдоп = y×Dq, где y - коэффициент влияния; Dq - отклонение от нормальных условий.
Погрешность прибора в реальных условиях его эксплуатации называется эксплуатационной и складывается из его основной погрешности и всех дополнительных и может быть, естественно, много больше его основной погрешности. Таким образом, деление погрешностей на основную и дополнительные является чисто условным и оговаривается в технической документации на каждое средство измерений.
Погрешность, обусловленная взаимодействием средств измерений и объекта измерения. Подключение средства измерений к объекту измерений во многих случаях приводит к изменению значения измеряемой величины относительно того значения, которое она имела до подключения средства измерения к объекту измерений и определение которого является целью измерений. Эта составляющая зависит от свойств средства измерений и объекта измерений.
В тех случаях, когда средство измерения используется для измерения постоянной или переменной во времени величины для его характеристики используют понятия статической и динамической погрешностей.
Статическая погрешность - это погрешность средства измерения, используемого для измерения постоянной величины. Например, погрешности, возникающие при измерении постоянного напряжения или частоты генератора образцовых частот, являются статическими погрешностями.
Динамическая погрешность. Динамическая погрешность средства измерения - это разность между погрешностью средства измерений в динамическом режиме и его статической погрешностью, соответствующей значению величины в данный момент времени. Она обусловлена реакцией средства измерения на скорость (частоту) изменения входного сигнала. Эта погрешность зависит от динамических свойств (инерционности) средства измерения, частотного спектра входного сигнала, изменений нагрузки и влияющих величин. На выходной сигнал средства измерений влияют значения входного сигнала и любые изменения его во времени. Различают полную и частную динамические характеристики.
Полная динамическая характеристика — характеристика, полностью описывающая принятую математическую модель динамических свойств средства измерений и однозначно определяющая изменение выходного сигнала средства измерений при любом изменении во времени информативного или неинформативного параметра входного сигнала или влияющей величины. Полную динамическую характеристику аналоговых средств измерений выбирают из следующих характеристик: дифференциального уравнения, передаточной функции, импульсной и переходной характеристик, амплитудно-фазовой, амплитудно-частотной характеристик.
При линейном, экспоненциальном и прямолинейном изменении входной величины для нахождения динамической погрешности используют операторную форму записи.
Абсолютная динамическая погрешность при этом определяется как
 , ,
где Sp(p) и Sи(p) - операторные чувствительности реального и идеального средств измерений соответственно.
Идеальным в динамике принято считать линейное безынерционное звено, т.е. звено, осуществляющее преобразование изменения величины без искажений.
Относительная динамическая погрешность имеет вид
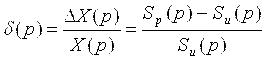 . .
При гармонических входных величинах пользуются понятиями амплитудно-частотной и фазочастотной погрешностей.
Амплитудно-частотная погрешность  определяется выражением определяется выражением
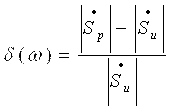 , ,
где 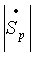 и и 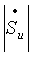 - модули комплексной чувствительности реального и идеального средств измерения соответственно. - модули комплексной чувствительности реального и идеального средств измерения соответственно.
Фазочастотная погрешность определяется как разность между фазочастотными характеристиками реального и идеального средств измерения:
Dj = jр (w) - jи (w).
Частная динамическая характеристика - любой функционал или параметр полной динамической характеристики. К частным динамическим характеристикам аналоговых средств измерений можно отнести время реакции, коэффициент демпфирования, значение амплитудно-частотной характеристики на резонансной частоте.
Для аналого-цифровых и цифроаналоговых преобразователей используются другие динамические характеристики.
Ряд метрологических характеристик подлежит нормированию с целью единообразного определения результатов измерений и оценки погрешностей измерений.
-
Нормирование метрологических характеристик средств измерений
Средства измерений можно использовать по назначению, если известны их метрологические свойства. Последние обычно описывают путем указания номинальных значений тех или иных характеристик и допускаемых отклонений от них.
Эти сведения приводят в нормативно-технической документации на средства измерений, а наиболее важные из них указывают на самих средствах.
Установление номинальных значений и границ допускаемых отклонений реальных метрологических характеристик средств измерений от их номинальных значений - нормирование метрологических характеристик.
Общим вопросам нормирования метрологических характеристик средств измерений посвящен ГОСТ 8.009—84 «Нормирование и использование метрологических характеристик средств измерений». Стандарт устанавливает номенклатуру метрологических характеристик средств измерений.
Характеристики, предназначенные для определения результатов измерений (без введения поправки):
1) функция (статическая характеристика) преобразования измерительного преобразователя, а также измерительного прибора с неименованной шкалой;
2) значение однозначной или значения многозначной меры;
3) цена деления шкалы измерительного прибора или многозначной меры;
4) вид выходного кода, число разрядов кода, цена единицы наименьшего разряда кода цифровых средств измерений.
Характеристики погрешностей средств измерений:
1) характеристики систематической составляющей погрешности;
2) характеристики случайной составляющей погрешности;
3) характеристики погрешности.
Характеристики чувствительности средств измерений к влияющим величинам:
2) изменения значений метрологических характеристик средств измерений, вызванных изменениями влияющих величин в установленных пределах.
Динамические характеристики средств измерений:
1) полная; 2) частные.
Характеристики взаимодействия средств измерений с объектом исследования и нагрузкой:
1) входное полное сопротивление; 2) выходное полное сопротивление.
Неинформативные параметры выходного сигнала средств измерений.
Из указанного перечня для конкретных средств измерений выбирают такие характеристики, которые достаточны для оценки погрешностей измерений.
-
Способы выражения пределов допускаемых погрешностей средств измерений
В настоящее время для большинства электрических средств измерений, используемых в статическом режиме, нормируют пределы допускаемых погрешностей.
Пределом допускаемой погрешности (допускаемой погрешностью) средств измерений называется наибольшая (без учета знака) его погрешность, при которой это средство может быть признано годным и допущено к применению. Например, пределы допускаемой приведенной погрешности вольтметра класса точности 1,0 равны ± 1 % верхнего предела измерений [6].
Вопросы нормирования погрешностей средств измерений рассмотрены в ГОСТ 8.401—80 «Классы точности средств измерений. Общие требования».
Согласно этому стандарту, пределы допускаемых основной и дополнительных погрешностей выражают в форме приведенных, относительных или абсолютных погрешностей. Форма представления пределов допускаемых погрешностей выбирается в зависимости от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения средств измерений.
Пределы допускаемой абсолютной основной погрешности устанавливают по формуле
DХдоп = ± a, (3.17)
если граница погрешностей средств измерений полагается практически неизменной в пределах диапазона измерения (присутствует чисто аддитивная составляющая погрешности) или
DХдоп = ± (a + bX), (3.18)
если границы погрешностей изменяются практически линейно (присутствует как аддитивная, так и мультипликативная составляющие погрешности). В этих формулах DXдоп – пределы допускаемой абсолютной основной погрешности, выраженной в единицах измеряемой величины или в делениях шкалы; X – значение измеряемой величины на входе (выходе) средств измерений или число делений, отсчитанных по шкале; a , b – постоянные положительные числа.
Пределы допускаемой абсолютной погрешности могут устанавливаться также по более сложной формуле или в виде графика, или в виде таблицы.
Пределы, допускаемой приведенной основной погрешности (в процентах) в случае присутствия только аддитивной составляющей погрешности устанавливают по формуле
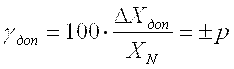 , (3.19) , (3.19)
где DХдоп - пределы допускаемой абсолютной основной погрешности, устанавливаемые по формуле (3.17); XN - нормирующее значение — условно принятое значение измеряемой величины, выраженное в тех же единицах, что и X; p - отвлеченное положительное число.
Правила выбора нормирующего значения XN :
 1. Для средств измерений с равномерной или степенной шкалой, а также для измерительных преобразователей, если нулевое значение входного (выходного) сигнала находится на краю или вне диапазона измерений, то нормирующее значение устанавливают равным большему из пределов измерений. В данном примере нормирующее значение ХN = 10. 1. Для средств измерений с равномерной или степенной шкалой, а также для измерительных преобразователей, если нулевое значение входного (выходного) сигнала находится на краю или вне диапазона измерений, то нормирующее значение устанавливают равным большему из пределов измерений. В данном примере нормирующее значение ХN = 10.
2. Если нулевое значение находится внутри диапазона измерений, то норми-
 рующее значение берется равным большему из модулей пределов измерений, т.е XN = 20 . рующее значение берется равным большему из модулей пределов измерений, т.е XN = 20 .
3. Для электроизмерительных приборов с равномерной шкалой, практически равномерной или степенной шкалой и нулевой отметкой внутри диапазона измерений XN допускается устанавливать равным сумме модулей пределов измерений:
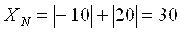 . .
Практически равномерная шкала - шкала, длины делений которой различаются не более чем на 30 %, а цена делений постоянна.
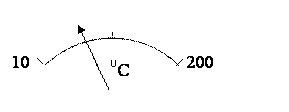 Степенная шкала - шкала с расширяющимися или сужающимися делениями и отличная от равномерной и практически равномерной шкалы. Степенная шкала - шкала с расширяющимися или сужающимися делениями и отличная от равномерной и практически равномерной шкалы.
- Для средств измерений, для которых принята шкала с условным нулем
(например, в градусах Цельсия), нормирующее значение устанавливают равным модулю разности пределов измерений, т.е. 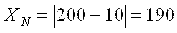 . .
5. Для средств измерений с установленным номинальным значением нормирующее значение равно этому номинальному значению.
6. Для измерительных приборов с существенно неравномерной шкалой (например, для омметров) нормирующее значение устанавливают равным всей длине шкалы или ее части, соответствующей диапазону измерений. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины.
Пределы допускаемой относительной основной погрешности (в процентах) устанавливают по следующим формулам:
а) в случае присутствия только мультипликативной составляющей погрешности 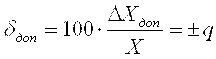 , (3.20) , (3.20)
если значение DХ установлено по формуле (3.17);
б) в случае присутствия соизмеримых аддитивной и мультипликативной составляющих погрешностей:
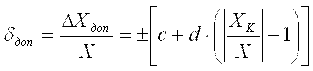 , (3.21) , (3.21)
если значение DХ установлено по формуле (3.18). В этих выражениях q - отвлеченное положительное число; XK - больший (по модулю) из пределов измерений;
с, d -положительные числа, причем 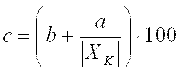 ; ; 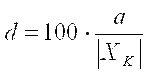 . .
В обоснованных случаях пределы допускаемой относительной основной погрешности устанавливают по более сложной формуле или в виде графика, или таблицы.
Значения р, q, с, d в формулах (3.19), (3.20) и (3.21) выбирают из ряда 1×10n; 1,5×10n; (1,6×10n); 2×10n; 2,5×10n; (3×10n); 4×10n; 5×10n; 6×10n (n = 1, 0, -1, -2 и т.д.). Значения, указанные в скобках, не устанавливают для вновь разрабатываемых средств измерений.
Пределы допускаемых дополнительных погрешностей устанавливают в виде:
а) постоянного значения для всей рабочей области влияющей величины;
б) отношения предела допускаемой дополнительной погрешности, соответствующего регламентированному интервалу влияющей величины, к этому интервалу;
в) предельной функции влияния;
г) функциональной зависимости пределов допускаемых отклонений от номинальной функции влияния.
Предел допускаемой вариации выходного сигнала и пределы допускаемой нестабильности выражают в виде доли допускаемой основной погрешности.
Способы выражения остальных метрологических характеристик устанавливаются в стандартах на средства измерений конкретного вида.
-
Классы точности средств измерений
Рассмотренные метрологические характеристики позволяют выявить такую качественную характеристику как точность средств измерений, положенную в основу деления средств измерений на классы точности.
Класс точности средства измерений - это его обобщенная характеристика, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами средств измерений, влияющими на точность, значения которых устанавливаются в стандартах на отдельные виды средств измерений.
Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств.
Общие положения о делении средств измерений на классы точности и способы нормирования метрологических характеристик регламентированы ГОСТ 8.401—80. Однако этот стандарт не устанавливает классы точности средств измерения, для которых предусмотрены нормы отдельно для систематической и случайной составляющих погрешности, а также если необходимо учитывать динамические характеристики.
Если класс точности прибора установлен по пределу допускаемой относительной основной погрешности, т.е по значению погрешности чувствительности [см. формулу (3.20)] и форма полосы погрешности принята чисто мультипликативной, обозначаемое на шкале значение класса точности обводится кружком. Например, обозначает, что dдоп = 1,5 %.
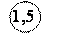 Если же полоса погрешности принята аддитивной и прибор нормируется по пределу допускаемой приведенной основной погрешности [см. формулу (3.19)], т.е. по значению погрешности нуля (таких приборов большинство), то класс точности указывается на шкале без каких-либо подчеркиваний. Например, 1,5 обозначает, что gдоп=1,5 %. Если же полоса погрешности принята аддитивной и прибор нормируется по пределу допускаемой приведенной основной погрешности [см. формулу (3.19)], т.е. по значению погрешности нуля (таких приборов большинство), то класс точности указывается на шкале без каких-либо подчеркиваний. Например, 1,5 обозначает, что gдоп=1,5 %.
Если шкала прибора неравномерная (например, у омметров), предел допускаемой основной приведенной погрешности выражается формулой (3.19), а нормирующее значение принято равным длине шкалы или ее части, класс точности обозначается на шкале одним числом, помещенным между двумя линиями, расположенными под углом. Например, 1,5 , это означает, что gдоп=1,5 %.
 Если средство измерений обладает как аддитивной, так и мультипликативной полосой погрешности, а пределы допускаемой относительной погрешности в процентах устанавливаются формулой (3.21), например, Если средство измерений обладает как аддитивной, так и мультипликативной полосой погрешности, а пределы допускаемой относительной погрешности в процентах устанавливаются формулой (3.21), например,
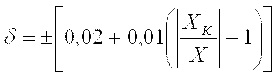 , ,
где с = 0,02; d = 0,01, то обозначение в документации будет «класс точности
0,02/0,01», а на приборе 0,02/0,01. Таким образом, для средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме относительных погрешностей [см. формулу (3.21) ], классы точности обозначают числами с и d (в процентах), разделяя их косой чертой.
Для средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме абсолютных погрешностей по формулам (3.17) или (3.18) или относительных в виде графика, таблицы или формулы, отличной от формул (3.20) и (3.21), классы точности обозначают прописными буквами латинского алфавита или римскими цифрами. Классы точности, которым соответствуют меньшие пределы допускаемых погрешностей, должны обозначаться буквами, находящимися ближе к началу алфавита, или цифрами, означающими меньшие числа.
Для всех рассмотренных случаев вместе с условным обозначением класса точности на шкале, щитке или корпусе средств измерений наносится номер стандарта или технических условий, устанавливающих технические требования на эти средства измерений.
Классы точности цифровых измерительных приборов со встроенными вычислительными устройствами для дополнительной обработки результатов измерений устанавливают без режима обработки.
При указании классов точности на измерительных приборах с существенно неравномерной шкалой допускается указывать пределы допускаемой основной относительной погрешности для части шкалы, лежащей в пределах, отмеченных специальными знаками, например точками или треугольниками.
Таким образом, обозначение класса точности средства измерений дает достаточно полную информацию для вычисления приближенной оценки погрешностей результатов измерений.
.
Ваш комментарий о книге
Обратно в раздел Наука
|
|
