Библиотека
Теология
КонфессииИностранные языкиДругие проекты |
Ваш комментарий о книге Мусаев А. Библия для адъюнктов и соискателей. Как подготовить и защитить кандидатскую диссертацию: методическое пособиеОГЛАВЛЕНИЕГЛАВА 5.
|
 |
ир случайный расположен |
![]()
"Здесь вам не тут - здесь вас быстро отвыкнут
водку пьянствовать и безобразия нарушать."
Жизнь сталкивает человека (и соискателя в том числе) со случайностью на каждом шагу. Все наше будущее в той или иной форме случайно. Прошлое, напротив, строго детерминировано, как детерминирована любая конкретная реализация. Однако в рамках того полуабстрактного и размытого интервала времени, беззастенчиво отторгнутого от прошлого и будущего, которое каждый человек называет своим "настоящим", будущее, ближайшее и отдаленное, имеет несравненно большее значение, чем его определившееся, навсегда детерминированное прошедшее. И уж конечно, вся научная деятельность человека обращена сугубо в его вероятностное будущее.
По-видимому, природа будущего многовариантна, и, следовательно, на него можно влиять путем принятия тех или иных решений. При этом формирование решений, в том числе и научных, осуществляется в условиях неопределенности, характеризуемой отсутствием достаточных знаний как об окружающей среде, так и о внутренних, для анализируемой ситуации (системы) процессах. Именно отсутствие необходимого объема знаний провозглашалось основным и единственным генезисом случайности. Принцип детерминизма, сформулированный П.Лапласом в его сочинении "Опыт философии теории вероятностей", утверждает, что при обладании необходимым объемом достоверной информации любое событие в будущем является абсолютно прогнозируемым. Так, например, результат пресловутого подбрасывания монетки, превратившегося в символ генерации событий с 50%-ной вероятностью реализации, вполне может быть предсказан, если точно знать значение полученного механического импульса, расположение точки его приложения относительно центра масс, высоту руки над поверхностью падения, характеристики твердости и гладкости поверхности и многое, многое другое.
Вывод детерминистов достаточно очевиден: понятие случайности является субъективным и существует лишь в сознании человека, недостаточно образованного и недостаточно понимающего окружающий однозначный мир.
Следует заметить, что идея детерминизма была провозглашена философами задолго до Лапласа. Так, Аристотель писал: "Ничто не делается случайно. Для всего, возникновению чего мы приписываем самопроизвольности или случаю, имеется некоторая определенная причина."
Однако в том и заключалось диалектическое величие древнегреческих мыслителей, что они умели для каждого мудрого тезиса находить и обосновывать не менее убедительный антитезис. Говоря словами Протагора, "каждому рассуждению противостоит равносильное." И вот он, антитезис Ксенофана: "Нет, достоверно никто никогда ничего не узнает."
Тем не менее идея лапласовского детерминизма довольно долго властвовала в науке, не имея достаточно убедительных источников тотальной, ничем не обусловленной случайности. И лишь поистине величайшие открытия физики XX столетия в мире микрочастиц позволили отыскать источники "первозданной" неопределенности. Впрочем, в мире, где разрушены даже причинно-следственные связи, можно, при желании, найти все, что угодно. В том числе - и самого Нечистого, творца Хаоса.
Следует заметить, что математики не отстали от своих физических "братьев по разуму" и отыскали "беспричинно" случайные процессы внутри так называемых странных аттракторов, возникающих при решении некоторых нелинейных дифференциальных уравнений [53, 85].
Разумеется, для большинства прикладных наук вопрос о генезисе случайности является вторичным. Важно другое - научиться принимать, поелику возможно, разумные решения в этом случайном мире, используя современную научную методологию, прежде всего математическую. Проблема оказалась настолько важной, что, по мнению Н.Винера, обобщается на всю формализованную методологию: "... высшее назначение математики как раз и состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает." При этом, как указано в [36], теория вероятностей дает не только и не столько вычислительный аппарат, сколько более широкую концепцию, позволяющую найти порядок и закономерность там, где классический детерминистический подход оказывается бессильным. Она предлагает более широкое понимание причинных связей, чем это делает любая детерминистическая теория.
Как отмечалось выше, интерес к случайности обнаруживается уже в трудах великих мыслителей древнего мира - Демокрита, Платона, Аристотеля. Известно, что статистические выводы общего характера делались в древнем Китае еще в 2238г. до н.э., в эпоху императора Яо на основе анализа результатов переписи населения в Поднебесной. Однако мысль о возможности характеризовать числом и мерой степень случайности возникла гораздо позднее, в районе XVI-XVII вв.
С диалектической терпимостью отметим, что азартные игры послужили мощным стимулятором развития вероятностной науки. Так, в "Божественной комедии" Данте указывается на попытки подсчитать число благоприятных исходов при игре в кости. В своем письме к Ф. ван Схоутену (1657), автору книги "О расчетах в азартных играх", Христиан Гюйгенс отмечает: "...я полагаю, что при внимательном изучении предмета читатель заметит, что имеет дело не только с игрой, но что здесь закладываются основы очень интересной и глубокой теории." Тотальную значимость вероятностной концепции достаточно быстро поняли и философы. Так, уже в 1687 г. был опубликован трактат Б.Спинозы "Заметки о математической вероятности."
Основателями теории вероятностей, по-видимому, следует считать замечательных французских математиков XVII в. Б.Паскаля и П.Ферма. Инициацией исследований для Паскаля послужила задача кавалера де Мере. Суть вопроса состояла в следующем: как по-справедливости" разделить начальные ставки между игроками (имеющими разное количество выигранных партий), закончившими игру до завершения заранее оговоренного общего числа партий.
Наряду с вероятностными методами в трудах ученых-демографов XVII в. Д.Граунта и У.Петти закладывались начала математической статистики.
Дальнейшее развитие теории вероятностей и математической статистики связано с именами Я.Бернулли, А. де Муавра, Монмора, Н.Бернулли, Д.Бернулли, Л.Эйлера, Т.Байеса, Ж.Даламбера и других корифеев мировой математики. Русская школа теории вероятностей хорошо известна трудами П.Л.Чебышева, М.В.Остроградского, В.Я.Буняковского, А.Н.Колмогорова и других. Впервые курс теории вероятностей в России был введен решением Совета Михайловской артиллерийской академии в Санкт-Петербурге в 1858 г. и прочитан ее слушателям профессором М.В.Остроградским. Впрочем, это далеко не единственный случай, когда потребности военной науки стимулировали развитие и прогресс вероятностной методологии.
 |
вероятностных пространствах |
"Копать от забора и до обеда!"
Характерной чертой любых открытых систем, в том числе и информационных, является наличие случайных входных воздействий. Это объясняется тем, что, во-первых, информационный процесс обязан нести в себе заданный уровень неопределенности (в противном случае он не будет содержать в себе никакой информации для потребителя), а во-вторых, информация передается на основе использования конкретных физических носителей - сигналов, подверженных воздействию различных неустойчивых факторов.
Результатом функционирования информационных систем (ИС) является решение, полученное на основе выбора из некоторого априорного множества решений. При этом под статистическим синтезом ИС понимается процесс формирования процедур принятия решения, обеспечивающих экспериментальное значение показателя качества на основе имеющейся входной информации. Указанный экстремум, как правило, является условным и связан с некоторой совокупностью априорных ограничений, определяемых выбранной моделью реальной ситуации.
В качестве основного подхода к задаче статистического синтеза ИС используется теория статистических решений [5, 6, 10, 16, 17, 25, 27 и др.].
Указанная теория дает естественный язык, на котором можно формировать задачи синтеза информационных систем. Общая теория статистических решений не связана с конкретным видом задач и обеспечивает нахождение оптимальных стратегий, определяющих как структуру синтезируемых систем, так и наилучшее значение их параметров. Кроме того, теория статистических решений позволяет на базе единой методологии анализировать свойства изучаемых систем, сравнивать различные варианты построения, а также с общих позиций оценивать сами подходы к синтезу ИС, подверженных случайным возмущениям.
Основным понятием в теории синтеза стохастических ИС является статистическая структура ![]() , где {W} - пространство наблюдений (выборочное пространство), {F} - пространство событий, или семейство подмножеств {W}, замкнутых относительно операций дополнения, пересечения и объединения (s-алгебра), и {P} - семейство вероятностных мер (распределений), заданных на {F}. Определение количественных или качественных характеристик этой меры служит основанием для принятия конкретных статистических решений.
, где {W} - пространство наблюдений (выборочное пространство), {F} - пространство событий, или семейство подмножеств {W}, замкнутых относительно операций дополнения, пересечения и объединения (s-алгебра), и {P} - семейство вероятностных мер (распределений), заданных на {F}. Определение количественных или качественных характеристик этой меры служит основанием для принятия конкретных статистических решений.
С точки зрения конкретной информационной системы результатом статистического решения является оценка ситуации, характеризуемой некоторым параметром (возможно, векторным) Q из пространства ситуаций (пространства параметров) {Q}. Параметрический подход к заданию статистической структуры нашел широкое применение в задачах анализа и синтеза систем. При этом семей-
ство мер P={F(Q), QI{Q}} считается заданным с точностью до параметров Q, причем вероятностной мере F(Q) при каждом фиксированном значении QI{Q} однозначно соответствует распределение вероятностей. Отсюда вытекает, что задачи параметрического синтеза ИС сводятся к принятию решения о значении неизвестного в общем случае векторного параметра QI{Q} исходя из полученных наблюдений x1,...,xn. В качестве решения в различных задачах теории систем могут выступать оценки скалярной или векторной величины, например векторы состояний системы, данные прогноза, результаты идентификации систем, статистические выводы о принятии гипотез, (в задачах обнаружения сигнала).
В настоящее время задача статистического синтеза ИС конкретизируется чаще всего к виду задачи синтеза обнаружителя сигнала или синтеза измерителя тех или иных параметров сигнала (радиосигнала). Однако следует иметь в виду, что к указанным формулировкам сводятся задачи синтеза систем, предназначенных для обеспечения весьма разнообразных функций:
Если речь идет о статистическом синтезе, то в общей постановке задачи следует говорить не о синтезе "обнаружителя", "измерителя" и т.п., а о синтезе системы в целом. При такой постановке задачи синтеза естественно требование согласования элементов системы для всех ее сечений:, например, не только по входу (согласование наблюдаемого процесса и устройства обработки), но и по выходу (согласование радиосигнала и среды) и т.д. [71, 72].
Задача статистического решения определяется заданием статистической модели (например, x1,...,xn - независимые одинаково распределенные случайные величины с общей плотностью f(x,Q), xI{R1}, QI{Q}I{Rm}, где {Rm} - m-мерное вещественное евклидово пространство) и пространства решений {D}. Предполагается, что информация о Q нужна для принятия решения d из указанного заранее множества решений {D}. В общем случае d - это результат той или иной процедуры обработки и определенная его интерпретация. Так, например, в задаче точечного оценивания значения сигнала по результатам измерений x1,...,xn с аддитивными шумами x1,....xn решением d будет сама оценка Qn.
Стратегией (решающей функцией) называется отображение S: {Rn}®{D}, т.е. правило, по которому в рамках данной статистической модели набору выборочных значений x1,...,xn соответствует решение dI{D}. Стратегия, по существу, и есть процедура обработки наблюдаемого процесса вместе с правилом интерпретации результата.
Фундаментальной задачей статистического синтеза систем является выбор стратегии в задаче статистического решения, которая была бы оптимальна относительно некоторой конкретной меры качества. Такой выбор требует введения в класс всех стратегий отношения порядка "больше - меньше", "лучше - хуже".
Стратегия S оптимальна в заданном классе стратегий {S}, если она превосходит по выбранной мере качества любую другую стратегию из этого класса. Стратегия S? допустима , если в заданном классе не существует строго превосходящей ее другой стратегии.
Самый распространенный способ упорядочения множества стратегий требует задания функции потерь W(Q,d), осуществляющей отображение {Q x Д} ® {R+}, где {R+} - положительная полуось {R1}, имеющая смысл ущерба от принятия решения d в условиях, когда истинное значение параметра есть Q.
В задачах оценивания в качестве функции потерь часто используют полный квадрат ошибки
![]() (5.1)
(5.1)
т.е. квадрат евклидова расстояния между d=Qn и Q. Иногда (5.1) усложняют и рассматривают
![]()
где l(Q) выбирается из условия конкретной задачи.
Каждой стратегии S ставится в соответствие средний ущерб, или риск Rs(Q)=E[W(Q,d)], где E[.] - символ математического ожидания. В случае точечного оценивания вектора параметров системы Q по независимой выборке измерений (x1,...,xn) с плотностью распределения f(x,Q)
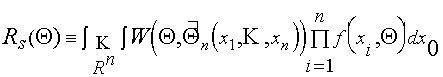
Для (5.1) риск называется средним квадратом ошибки
![]() где
где ![]() - дисперсия
- дисперсия ![]() .
.
В задачах параметрического синтеза ![]() часто ограничивается классом асимптотически несмещенных, асимптотически нормальных оценок, т.е. стратегия S, приводящая к такой оценке, для которой при n®? для любых x
часто ограничивается классом асимптотически несмещенных, асимптотически нормальных оценок, т.е. стратегия S, приводящая к такой оценке, для которой при n®? для любых x
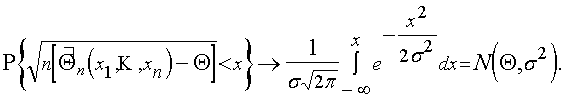
Риск здесь связан с вероятностным рассеянием Qn около истинного значения Q, а для нормального закона существует естественная мера рассеяния - дисперсия, поэтому в качестве функции риска в асимптотических исследованиях используют
![]()
При ограниченных выборках наблюдений естественной общей меры рассеяния не существует и выбор приходится осуществлять, сообразуясь с условиями конкретной задачи.
Риск Rs(Q) задает в множестве стратегий частичное упорядочение так, что
![]() для всех QI{Q}.
для всех QI{Q}.
Как правило, кривые ![]() и
и ![]() оказываются пересекающимися и, значит, соответствующие стратегии в целом несравнимы. Лишь в очень редких случаях можно рассчитывать на существование в данном классе кривой, лежащей равномерно (при всех Q) ниже всех остальных и соответствующей тем самым оптимальной стратегии.
оказываются пересекающимися и, значит, соответствующие стратегии в целом несравнимы. Лишь в очень редких случаях можно рассчитывать на существование в данном классе кривой, лежащей равномерно (при всех Q) ниже всех остальных и соответствующей тем самым оптимальной стратегии.
Рассмотрим теперь особый случай, когда по существу задачи параметр Q сам есть случайная величина. Статистическая модель здесь имеет следующий вид: дан случайный вектор (Q,x1,...,xn) с (n+1)-мерной плотностью распределения A(Q,x1,...,xn). В результате эксперимента получена одна реализация этого вектора, в которой компоненты x1,...,xn являются наблюдаемыми, а Q - ненаблюдаемой. Требуется дать прогноз значения Q на основе значений x1,...,xn.
Очевидно, плотность распределения Q можно записать в виде
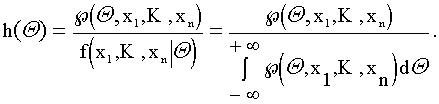
В качестве оценки могут выступать различные числовые характеристики распределения: математическое ожидание, мода, медиана и т.п.
Обычно задача рассматривается в упрощенной постановке, когда измерения x1,...,xn - независимые одинаково распределенные случайные величины с общей плотностью f(x,Q), а Q - не зависимая от них случайная величина с плотностью g(Q), так что
![]()
![]() (5.2)
(5.2)
Функцию g(Q) называют априорной, h(Q) - апостериорной плотностью величины Q. Данную особую форму постановки задач математической статистики называют байесовской. Она обладает многими положительными чертами, поскольку позволяет учитывать с помощью распределения g(Q) ту априорную информацию о неизвестном параметре, которая всегда в той или иной форме имеется у наблюдателя. При таком подходе оказывается целесообразным введение понятий априорного и апостериорного байесовского риска.
Априорным байесовским риском называется величина
![]()
(усреднение по выборке наблюдений и по априорному распределению Q). В случае (5.2)
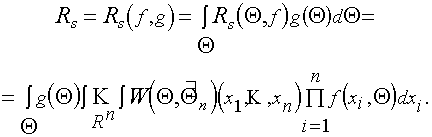 (5.3)
(5.3)
Функция потерь W и априорное распределение g задают в множестве стратегий байесовское упорядочение:
8 Зак. 92
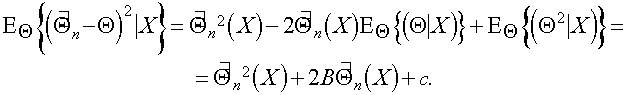
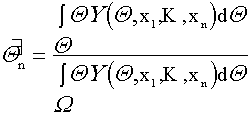
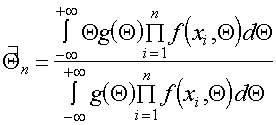
"Сейчас разберусь, как следует, и накажу кого попало."
Теория статистических решений, используемая для синтеза ИС, позволяет строить процедуры, реализация которых приводит к формированию искомых решений, и анализировать их свойства. При этом принятие решения представляет собой процедуру выбора решения d из пространства {D} на основе результатов наблюдений интересующей нас ситуации Q из пространства ситуации Q [102, 103]. Однако в реальной обстановке параметр Q не может наблюдаться непосредственно и суждение о нем выносится на основе технически доступных наблюдений w I W, функционально связанных с Q.
В качестве примера рассмотрим процесс определения трехмерной траектории подвижного объекта, движущегося с постоянной скоростью, по данным измерений. Решение представляет собой оценку вектора параметров траектории ![]() на некоторый момент времени t=t0, в данном случае в прямоугольной декартовой системе координат (наблюдения w в этом случае представляют собой измерения дальности, радиальной скорости, угловых координат и т.д.).
на некоторый момент времени t=t0, в данном случае в прямоугольной декартовой системе координат (наблюдения w в этом случае представляют собой измерения дальности, радиальной скорости, угловых координат и т.д.).
Наличие возмущающих воздействий, оказываемых средой на любую реальную систему, приводит к тому, что имеющиеся наблюдения практически всегда содержат вероятностную составляющую. При этом связь наблюдений с вектором параметров может быть задана с помощью некоторого, в общем случае нелинейного оператора a:
w = a (Q,x) , w I {W}, Q I {Q}.
Выбор решения dI{D} осуществляется на основе наблюдений w I W и априорной информации, имеющейся в распоряжении обработчика. Таким образом, процедура принятия решения, формирование которой является основным предметом статистического синтеза, может быть записана в виде оператора S: ![]()
Общая схема принятия статистических решений представлена на рис.5.1. В идеальном случае оператор S выполняет функцию обращения a. Причем качество реализации этого обращения в значительной степени зависит от наличия и достоверности априорной информации. Наличие того или иного объема достоверной априорной информации задает уровень неопределенности, при которой принимается решение.
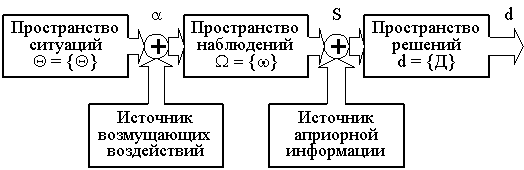
Рис. 5.1. Общая схема принятия статистических решений
Наиболее полным уровнем априорной информации является наличие вероятностного описания пространств {W} и {Q} с помощью априорного распределения h(Q) и семейства распределений ![]() для всех QI{Q}. В этом случае решение выбирается в соответствии с байесовским упорядочением стратегий (5.4), причем правило предпочтения строится на основе байесовского риска (5.3). Подобный подход обеспечивает наиболее эффективное решение. Однако в большинстве практических ситуаций априорной информации недостаточно для задания h(Q). Тогда переходят к стратегиям, не использующим информацию об h(Q), т.е. способным обеспечить рациональное решение в условиях более высокого уровня априорной неопределенности.
для всех QI{Q}. В этом случае решение выбирается в соответствии с байесовским упорядочением стратегий (5.4), причем правило предпочтения строится на основе байесовского риска (5.3). Подобный подход обеспечивает наиболее эффективное решение. Однако в большинстве практических ситуаций априорной информации недостаточно для задания h(Q). Тогда переходят к стратегиям, не использующим информацию об h(Q), т.е. способным обеспечить рациональное решение в условиях более высокого уровня априорной неопределенности.
В качестве основного подхода к поиску решений при известной функции распределения измерений с плотностью f(x-Q) используется метод максимального правдоподобия (ММП) [62]. Идея метода сводится к нахождению решения, минимизирующего функцию правдоподобия
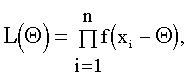 (5.5)
(5.5)
где xi, i=1,...,n, - наблюдения, полученные в результате измерений.
Как показано в классических курсах математической статистики [52, 61], такое решение является наилучшим с точки зрения минимизации дисперсии оценки. Само решение отыскивается путем применения численных методов к системе уравнений правдоподобия
![]() (5.6)
(5.6)
где ![]() - градиент функции по Q.
- градиент функции по Q.
В некоторых случаях решение (5.6) может быть получено в явном виде. В качестве примера рассмотрим описанную в этой главе схему определения параметров движения по данным измерений y, связанных с ними линейной моделью вида y=AQ+x, где А - постоянная матрица, x- вектор аддитивных погрешностей измерений.
Предположим, что x значения подчинены центрированному нормальному закону распределения с дисперсией s2. Тогда в соответствии с (5.5) искомое решение d=Q будет представлять собой аргумент, минимизирующий значение функционала
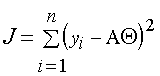 (5.7)
(5.7)
Совокупность различных алгоритмов, предназначенных для минимизации квадратичных функционалов вида (5.7), известна в статистическом анализе под названием метода наименьших квадратов (МНК) [73]. В данном случае соотношения (5.6), называемые в теории МНК системой нормальных уравнений, приводят к нахождению оценки в явном виде:
![]() (5.8)
(5.8)
В ситуациях, когда измерения являются неравноточными с дисперсиями (s12,...,sn2), в выражение (5.8) входит диагональная весовая матрица P=diag(s12,...,sn2). Заметим, что при определении параметров орбит обычно имеют не линейную, а лишь линеаризованную зависимость между измерениями и оцениваемыми параметрами, в результате оценка находится итерационно: ![]() , а в качестве наблюдений выступают невязки
, а в качестве наблюдений выступают невязки ![]() между данными, соответствующими опорной орбите, полученной в результате прогнозирования (экстраполяции), и реальными измерениями. Таким образом, окончательно искомую оценку можно записать в виде
между данными, соответствующими опорной орбите, полученной в результате прогнозирования (экстраполяции), и реальными измерениями. Таким образом, окончательно искомую оценку можно записать в виде
![]()
Требования к априорному значению распределения ![]() во многих практических случаях являются невыполнимыми. При этом переходят к следующему уровню неопределенности, полагая h(Q) и
во многих практических случаях являются невыполнимыми. При этом переходят к следующему уровню неопределенности, полагая h(Q) и ![]() неизвестными. Соответствующий математический аппарат, получивший наименование непараметрической статистики, практически не использует априорную информацию, считаются известными лишь различия между конкурирующими гипотезами о распределениях.
неизвестными. Соответствующий математический аппарат, получивший наименование непараметрической статистики, практически не использует априорную информацию, считаются известными лишь различия между конкурирующими гипотезами о распределениях.
Можно считать, что чем больше достоверной априорной информации используется процедурой, тем выше качество найденного решения, и в этом смысле байесовские оценки и оценки по ММП являются наилучшими. Однако это справедливо лишь при наличии именно достоверной априорной информации. Даже при незначительных отклонениях реальных характеристик от ошибочно принятой исходной модели их эффективность может существенно снизиться, т.е. указанные оценки оказываются статистически неустойчивыми. В то же время практически полный отказ от использования априорной информации, характерный для непараметрических методов синтеза, может привести к существенному снижению качества соответствующих процедур и, как следствие, всей ИС. В связи с этим возникает стремление к построению компромиссных методов статистического синтеза, способных без существенного снижения эффективности принимаемых решений устойчиво функционировать в условиях априорной неопределенности относительно вероятностных характеристик исходных данных.
Один из путей реализации такого направления основан на применении адаптивных методов, позволяющих перестраивать структуру процедуры, лежащей в основе функционирования ИС, или подбирать ее числовые параметры в соответствии с изменениями, происходящими в окружающей среде и в самой системе [31, 58, 89, 102, 103, 122]. Однако при использовании адаптивных алгоритмов всегда необходимо учитывать, что их применение предполагает наличие известной структурной, информационной или временной избыточности, что не всегда допустимо в реальных ситуациях.
В качестве альтернативы адаптивному подходу были предложены методы статистического синтеза, обладающие повышенной устойчивостью к нарушениям адекватности между априорной моделью и реальной ситуацией [12, 75, 76, 82, 108, 120]. Устойчивые методы позволяют синтезировать системы в заданном диапазоне изменений возмущающих воздействий без существенного снижения показателя качества. Одно из важнейших направлений в реализации этого подхода - применение принципа минимакса, идея которого сводится к построению наилучшего решения для наименее благоприятных условий. Минимаксный подход, по существу, является единственным методом, обеспечивающим в условиях неопределенности строгий математический результат. Идея минимакса обладает высоким уровнем общности, и на ее основе могут быть получены как частные случаи, так и многие современные методы статистического синтеза.
И завершим данный параграф очередным "мэрфологическим" откровением.
Правило Фалькланда: когда нет необходимости принимать решение, не следует этого делать.
 |
ешенье туго вызревает, |
"Что вы за ногти на ногах отрастили? Как у орла, хоть по деревьям лазай!"
В общем случае под адаптацией будем понимать процесс изменения параметров и структуры системы, а возможно и управляющих воздействий, на основе текущей информации с целью достижения определенного, обычно оптимального по некоторому критерию, состояния системы при начальной неопределенности и изменяющихся условиях работы [122].
При этом подразумевается, что система способна в зависимости от поступающей информации о среде и своем состоянии целенаправленно изменять собственное состояние или структуру, в результате чего возникает ответная реакция, направленная на повышение качества ее функционирования. В данном случае имеется в виду интегральный показатель качества, так как на отдельных этапах работы частные функциональные показатели качества в результате адаптации могут существенно снижаться. Примером может служить ситуация, когда вход радиоприемного устройства ИС закрывается при возникновении энергетических перегрузок, т.е. сводит к нулю показатель функциональной эффективности, однако в целом для данной ситуации выработанное решение является оптимальным.
Элементы адаптации, или приспосабливаемости к окружающей обстановке, характерны для большинства систем, функционирующих в реальной среде. При этом широкое разнообразие форм и методов адаптации ведет к обилию характеризационных признаков и существенно затрудняет классификацию адаптивных систем. Наиболее естественно различать адаптивные системы на основе самого механизма адаптации, позволяющего получать управляющую информацию и в соответствии с нею изменять параметры или структуру ИС. Для этого представим адаптивную систему в виде некоторой ИС (или системы управления (СУ)), взаимодействующей с окружающей ее средой (рис.5.2).
В результате указанного взаимодействия вырабатывается решение dвых. В устройстве сравнения результат этого решения или значение некоторой функции от него сравнивается со значением, полученным из задающего устройства. На основании разностного сигнала ![]() устройство управления вырабатывает воздействие, приводящее к требуемым изменениям в ИС. Если в результате воздействия предполагается изменение состояния системы, то в основе ИС лежит система с переменными параметрами, а если изменяется ее структура - то система с переменной структурой.
устройство управления вырабатывает воздействие, приводящее к требуемым изменениям в ИС. Если в результате воздействия предполагается изменение состояния системы, то в основе ИС лежит система с переменными параметрами, а если изменяется ее структура - то система с переменной структурой.
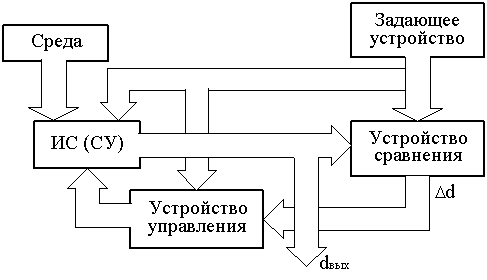
Рис. 5.2. Схема взаимодействия адаптивной системы со средой
Простейшими адаптивными системами являются системы без обучения. В них задающее устройство вырабатывает сигнал d(t) и ИС стремится к формированию сигнала dвых(t) такого, что ![]() . Подобные системы получили наименование следящих. В частном случае, при d(t)=const, имеем системы стабилизации.
. Подобные системы получили наименование следящих. В частном случае, при d(t)=const, имеем системы стабилизации.
Очевидно, сигнал управления может вырабатываться и на основе вычисления функционала J(dвых), причем процесс адаптации должен вызвать либо экстремизацию этого функционала J(dвых(t)) ® extr , либо превышение им некоторого порога J(dвых(t)) > J0.
Повышение автономности адаптивных систем приводит к процессам обучения, при которых выработка у системы определенного поведения в конкретных условиях осуществляется на основе обучения. При этом под обучением понимается изменение состояния под влиянием либо специализированных тестовых посылок с системой "поощрений" и "штрафов", формируемых задающим устройством (обучение с учителем), либо без них, а лишь на основе формально поставленной целевой функции, установленных ограничений и некоторой совокупности исходных правил (самообучение).
В тех ситуациях, когда изменяется не состояние, а структура ИС, имеем процессы организации и самоорганизации соответственно, когда же системы могут не только выбирать структуру из некоторой априорной совокупности, но и формировать принципиально новые структуры, их относят к категории развивающихся систем. Наиболее сложные формы адаптации реализуются в системах с искусственным интеллектом , в которых самостоятельными адаптивными свойствами обладают и задающее устройство, и устройство управления. Таким образом, классификация адаптивных систем может быть представлена в виде схемы, изображенной на рис. 5.3.
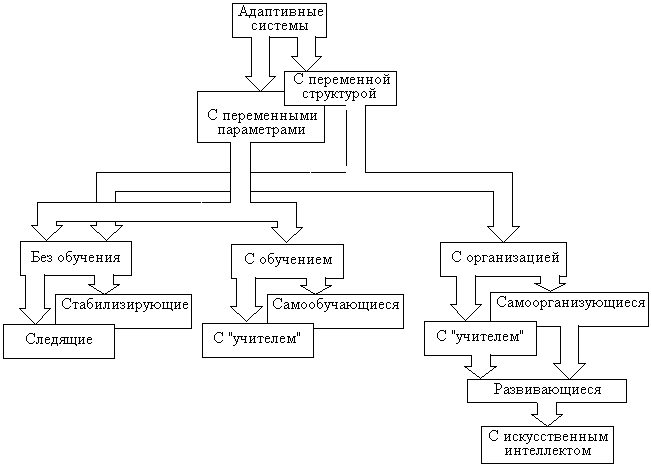
Рис. 5.3. Классификация адаптивных систем
Приведенная классификация адаптивных систем основана на технических аспектах адаптации и акцентирована на выделении принципиально важных ее сторон - наличии обратной связи и возможности регулирования параметров и структуры. Существуют и другие подходы к классификации, основанные на информационных аспектах или методах снижения энтропии системы.
С точки зрения статистического синтеза целесообразно различать задачи адаптации как задачи выбора на параметрических, непараметрических и робастных структурах.
При решении задач статистического синтеза ИС, заданных на параметрических структурах, т.е. в условиях, когда распределение случайных составляющих считается известным, центральный вопрос адаптации системы - определение или уточнение мешающих параметров. При этом под мешающими параметрами подразумеваются величины, которые не относятся к основным оцениваемым параметрам, однако их наличие является существенным с точки зрения базовой модели принятия решения и незнание этих параметров приводит, в конечном счете, к снижению эффективности функционирования системы.
В качестве примера можно привести задачу определения и прогноза движения космического аппарата (КА). Основные оцениваемые параметры составляют вектор из проекций векторов положения и скорости КА на оси прямоугольной геоцентрической системы координат
![]()
а к мешающим параметром можно отнести значения коэффициентов гармоник разложения гравитационного поля Земли, неравномерность вращения Земли, погрешности геодезической привязки измерительных станций, характеристики солнечной активности, влияющей на плотность атмосферы и величину солнечного ветра, и т.п. Таким образом, статистический синтез системы слежения за КА, использующий методологию параметрической адаптации, связан с дополнительным расширением вектора состояния ![]() путем включения в его состав указанных мешающих параметров. Это, в свою очередь, связано с увеличением необходимого объема измерений, времени наблюдения, вычислительных ресурсов и полосы пропускания следящей системы. Ничто не дается даром.
путем включения в его состав указанных мешающих параметров. Это, в свою очередь, связано с увеличением необходимого объема измерений, времени наблюдения, вычислительных ресурсов и полосы пропускания следящей системы. Ничто не дается даром.
Достаточно широкое распространение адаптивный подход нашел в задачах статистического синтеза на непараметрических структурах, т.е. при практическом отсутствии сведений о вероятностных законах распределения измерений и состояния системы. В этом случае идея адаптации основана на оценке функций распределения с вынесением предварительного решения, служащего исходной базой для нахождения оптимальных выводов.
Возможен и другой подход, при котором на основе текущей измерительной информации осуществляется нахождение неопределенного функционала - среднего показателя качества системы, зависящего от результата выбора параметров системы и совокупности измерений с неизвестным распределением [122]. Причем процесс адаптации реализуется в виде итерационных процедур градиентного поиска этого функционала. Выбор параметров адаптации на каждом шаге обеспечивает изменение показателя качества в направлении экстремума.
Следует заметить, что отказ от использования априорной информации и связанное с ним возрастание роли адаптации приводят к дополнительным требованиям - к временной информационной или структурной избыточности, что во многих практических задачах может оказаться недопустимым или нежелательным.
Альтернативный подход к решению задач статистического синтеза основан на робастных методах [68, 82, 108, 120], суть которых состоит в построении алгоритмов нахождения решения, обладающих повышенной устойчивостью и в то же время способных в максимальной степени использовать всю имеющуюся априорную информацию. Роль адаптации в этом случае состоит в выявлении достоверности имеющегося объема априорной информации либо в формировании решений, позволяющих выделять априорную информацию для заданного уровня достоверности. Так, например, при построении робастных оценок параметров сигналов на основе теории М-оценивания [120] адаптация может оказаться полезной для определения принадлежности закона распределения измерений к тому или иному классу распределения. При этом подобная классификация является процедурой существенно более простой, чем задача определения эмпирической функции распределения, характерная для непараметрического подхода. В результате роль адаптации в процедуре принятия решения существенно уменьшается, что, в свою очередь, снижает уровень требований к избыточной информации или к времени предварительного тестирования данных.

 |
оть эффект приспособленчества Адаптивность к возмущениям |
![]()
"Всех отсутствующих построить в одну шеренгу!"
Переход к устойчивым методам статистического синтеза и, в частности, к минимаксным методам, обусловлен наличием расхождений между априорной моделью, на основе которой строятся процедуры решения, и реальной ситуацией. Интерес к минимаксным методам объясняется тем, что хотя они и исходят из более широкой и реалистической модели, чем классические ветви оптимального математического синтеза, но используют всю имеющуюся, заведомо достоверную априорную информацию. Правильное применение минимаксных методов позволяет минимизировать потери при переходе к ним от оптимальных алгоритмов типа ММП. В то же время выигрыш от их применения при отклонениях реальных условий от априорной модели, т.е. в большинстве практических случаев, оказывается весьма существенным. При этом процедуры, получаемые на основе минимаксного подхода, достаточно просты с вычислительной точки зрения и могут быть реализованы на основе несложных специализированных вычислителей.
Рассмотрим задачу минимаксного синтеза ИС в общем виде. Пусть наблюдения w представлены выборкой измерений X=(x1,...,xn) с плотностью распределения f(x1,...,xn,Q), x1,...,xn c Rn, QI{Q}. Обозначим через R(Q,d) функцию риска
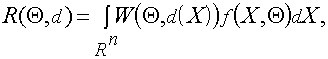
где W(Q,d)- заданная функция потерь.
Принцип минимакса состоит в том, что из множества возможных решений {D} выбирается то решение d*, для которого

Таким образом, минимаксный подход требует заранее ориентироваться на значение параметра Q, наименее благоприятное для данной задачи, принятия решения. При байесовском подходе это соответствует ориентации на самое неблагоприятное из возможных априорных распределений. Такой же принцип можно использовать и при других конструкциях функции риска. В частности, в случае неполного задания семейства плотностей f(x<Q) иногда удается получить минимаксную оценку, основанную на самой неблагоприятной из возможных плотностей.
В качестве примера применения минимаксного подхода в задачах статистического синтеза ИС рассмотрим задачу оценивания сигнала Q по результатам измерений (x1,...,xn), представляющим собой реализации случайной величины X с распределением F(x-Q). Пусть F(x) - непрерывное, симметричное, одновершинное распределение с плотностью f(x). В общем случае за оценку сигнала Qn принимают решение минимизационной задачи
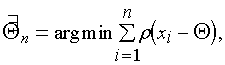 (5.9)
(5.9)
где r(xi-Q) - некоторая четная неотрицательная функция, оценивающая близость измерений xi к искомому центру распределения Q. Ее называют функцией контраста, а оценки Qn (5.9) - оценками минимального контраста, или М-оценками.
В частности, при r(z)=ln f(z) М-оценки совпадают с оценками максимального правдоподобия, а при r(z)=z2 - с оценками, полученными по МНК. Свойства М-оценок удобно формулировать в терминах производной от функции![]() . Если y(z) определена при всех z , то задача (5.9) сводится к решению уравнения
. Если y(z) определена при всех z , то задача (5.9) сводится к решению уравнения
![]() (5.10)
(5.10)
Для вполне реализуемых условий регулярности [76, 120] оценки, получаемые в результате решения (5.8) или (5.9), удовлетворяют условиям существования и единственности и обладают свойствами асимптотической нормальности и несмещенности, т.е.
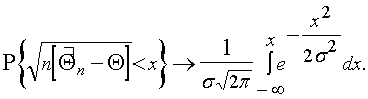
или
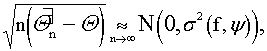
где s2(f,y) - асимптотическая дисперсия оценки Qn.
Можно показать [120], что в общем случае асимптотическая дисперсия ![]() имеет вид
имеет вид
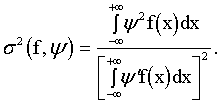 (5.11)
(5.11)
Интегрируя выражение в знаменателе (5.11) по частям и применяя к нему неравенство Коши-Буняковского, получаем
![]() (5.12)
(5.12)
где
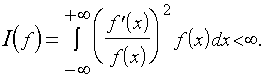 (5.13)
(5.13)
Соотношение (5.12) называется неравенством Рао-Крамера. Оно определяет нижнюю границу дисперсии для заданной плотности распределения f. Таким образом, функционал (5.13), называемый информацией Фишера, характеризует связь между распределением измерений и потенциальной границей (дисперсия оценки), построенной на их основе. Оценки, для которых (5.12) вырождается в равенство, называются эффективными. В частности, для r(z)=lnf(z), т.е. для оценок максимального правдоподобия (y(z)=const(f'(z)/f(z)), имеет место указанное равенство.
Предположим, что плотность распределения измерений f0 известна. Тогда в соответствии с изложенным применение ММП дает искомое решение в виде уравнения
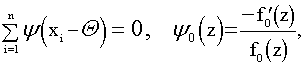
причем это решение является эффективным, т.е. наилучшим с точки зрения достижения минимума дисперсии оценки:
![]()
Однако в реальных ситуациях, связанных, например, с работой ИС в условиях сложной помеховой обстановки, распределение измерений неизвестно. Тем не менее наличие априорной информации позволяет вполне достоверно оценить класс распределений, к которому относится f(x). В частности, наиболее характерным для реальной помеховой обстановки (без преднамеренных помех) является класс засоренных нормальных распределений
![]() (5.14)
(5.14)
где fN - плотность нормального распределения.
Исходя из общих принципов минимакса поставим задачу: для заданного выпуклого множества распределений K найти "наименее благоприятное" распределение f0(K) , для которого имело бы место неравенство
![]()
или I(f) ? I(f0). Очевидно, эта задача сводится к минимизации функционала (5.13) на множестве K (5.14)
![]()
При этом если "наихудшее" распределение существует и принадлежит K, то выполняются равенства
![]()
где y = {Y} - некоторый класс функций, удовлетворяющих несложным условиям регулярности [76].
Таким образом, речь идет о существовании седловой точки у дисперсии s2(f,y) на {K u Y}. Если такая седловая точка существует, то говорят, что пара (f0, y0) решает проблему минимакса в {K u Y}.
Приведем несколько оценок минимального контраста, решающих эту проблему для некоторых классов K, хорошо зарекомендовавших себя при решении практических задач статического синтеза ИС.
1. Выборочная медиана
9 Зак. 92
n - четное,
n - нечетное;
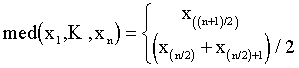
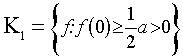 . Она является наиболее "осторожной" оценкой и обычно используется в качестве начального приближения в рекуррентных и адаптивных алгоритмах оценивания. Соответствующая ей функция y(z) =
. Она является наиболее "осторожной" оценкой и обычно используется в качестве начального приближения в рекуррентных и адаптивных алгоритмах оценивания. Соответствующая ей функция y(z) = 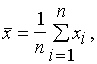
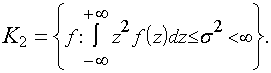
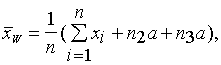
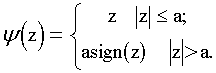
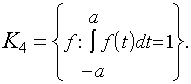
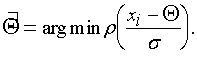 (5.15)
(5.15)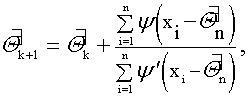 (5.16)
(5.16)
 |
инимаксная наука |
Ваш комментарий о книге
Обратно в раздел Наука
