Мусаев А. Библия для адъюнктов и соискателей. Как подготовить и защитить кандидатскую диссертацию: методическое пособие

ОГЛАВЛЕНИЕ

ГЛАВА 3. БАЗОВЫЕ КАТЕГОРИИ: СИСТЕМА И МОДЕЛЬ

"Ну как идет, как идет! Корова какая-то! Свинья, наверное."
В основе любых научных исследований лежат фундаментальные дисциплины, занимающие почетное место в учебных программах вузов и тем не менее достаточно серьезно забытые к моменту начала работы над диссертацией. Здесь нечему удивляться: память старательно самоочищается от всего, что не требуется в повседневной жизни. Однако теперь Вашим Повседневьем становится Наука, и нужно не только с усердием перетряхнуть архивы собственной памяти, но и постараться загрузить ее новыми фундаментальными знаниями. И здесь "во главе угла" встает Ее Величество Математика и ее прикладные ответвления - кибернетика, теория эффективности, исследование операций и т.п.
Следует иметь в виду, что "математика - не свод готовых ответов на любой вопрос. Математика - это скорее школа мышления" [127]. И важнейшим атрибутом такого мышления является системность, т.е. способность увидеть взаимосвязанное единство в совокупности разрозненных фактов, событий, элементов.

В соответствии с законами "мэрфологии" основные постулаты развитой теории систем имеют следующий вид:
1. Все - система.
2. Все - часть еще большей системы.
3. Вселенная бесконечно систематизирована как снизу вверх (все более крупные системы), так и сверху вниз (меньшие системы).
4. Все системы бесконечно сложны. (Иллюзия простоты возникает из-за сосредоточения внимания на одной или нескольких переменных.)

Главным инструментом изучения систем и связанных с ними процессов является модель. В теоретических исследованиях используются математические модели, в экспериментальных - натурные, полунатурные и т.п. Задача соискателя состоит в том, чтобы, применяя системную методологию, математическое или иное моделирование и другой арсенал научных исследований, решить стоящую перед ним научную проблему. А для начала следует вспомнить основные положения системного анализа и математического моделирования, для чего и написана настоящая глава.

одель и система - извечная пара: Здесь - жизнь, а вон там - - театральная драма, Там взлет к небесам, синева и паренье. А тут, на бумаге, - строка уравненья, Здесь мудрый ученый, а там только тень Неровным зигзагом легла на плетень... Модели, модели, повсюду модели, Как стереотипы, к душе прикипели, И радуют жизнь нам хмельной простотой, А как протрезвеешь... О, Боже ж ты мой!

3.1. Системный подход:
взаимосвязь всего со всем

"Лейтенант, в роте семь разгильдяев, а Вы волосы на пробор носите."
NB!: Начнем этот параграф с высказывания А.Эйнштейна: "Чисто математические построения позволяют найти те понятия и те закономерные связи между ними, которые дают ключ к пониманию явлений природы."

Важно отметить, что в приведенных словах указывается на необходимость исследования не только тех или иных явлений, но и совокупности всевозможных сопутствующих им взаимосвязей, без которых полученные решения не будут ни достаточно полными, ни достаточно корректными с точки зрения понимания изучаемого вопроса. Именно взаимосвязанность составных частей является основной характеристикой одного из важнейших объектов научных исследований - системы.
Понятие "система" представляет собой базовую научную категорию в самых разнообразных областях знаний. Существует множество определений этого понятия, различающихся между собой той или иной степенью неудачности. Само слово "система" произошло от греческого sistema - целое, составленное из частей. Наиболее общее, философское определение утверждает, что система - это множество элементов, находящихся в отношениях и связях друг с другом, которое образует определенную целостность, единство.
Характерными свойствами системы являются целостность, структурированность и (для большинства искусственных систем) целенаправленность. Свойство целостности говорит о том, что система отделена от внешней среды и находится во взаимодействии с нею. Структурированность означает, что система может быть разделена на подсистемы или составные элементы, связанные и взаимодействующие друг с другом. Свойство целенаправленности предполагает задание некоторой цели, достижение которой определяет предназначение системы.
Формализация понятия "система" приводит к более конкретным, хотя и более узким определениям. В частности, в кибернетике система задается в виде математических моделей или, где - множество входов, - множество состояний, - множество выходов.
Таким образом, систему можно трактовать, как некоторый "черный ящик", преобразующий входные сигналы (данные) в выходные в интересах некоторой априори заданной цели. В случае, когда функционирование системы изучается с точки зрения изменений ее состояния во времени, , где - интервал времени, система называется динамической. Если каждой входной функции соответствует единственная выходная функция, то такая система называется функциональной; в противном случае ее относят к категории неопределенных. Важнейшим свойством, присущим реальным системам, является причинность их эволюции. Это означает, что настоящее состояние системы не зависит от будущего при заданном прошлом. Иными словами, если при, то соответствующие им выходные сигналы будут удовлетворять требованию.

функциональный характер и не затрагивает ее структуру. В то же время в задачах синтеза важнейшую роль играет именно структура системы, которую и требуется
определить. В связи с этим обобщенная модель системы еще более усложняется и приобретает вид

	(3.1)

где - множество элементов системы; - матрица отношений между элементами системы, заданными на; - матрица отношений между множествами и (отношения эмерджентности). Составляющая часть системы  называется ее структурой, а  - ее программой функционирования. Таким образом, система представляет собой объединение этих двух составляющих, а ее единство определяется отношением эмерджентности.
Заметим, что понятие элемента системы является первичным и как всякое первичное представление очень сложно формализуется, но достаточно очевидно на уровне "здравого смысла": элемент - это составляющая часть системы на последней ступени ее детализации. Декомпозицию можно проводить до атомарного уровня и ниже; здесь, как и вообще в жизни, следует во время остановиться, не утратив функциональной осмысленности.
Следует заметить, что категория "система", несмотря на кажущуюся простоту, достаточно загадочна и малообъяснима с позиций материализма. Так, например, расширение системы вполне может привести к диалектическому скачку, описанному Георгом Вильгельмом Фридрихом Гегелем в XIX в., в результате которого образуется новое качество. При этом новое качество может быть совсем не присущим ни одному элементу, образующему эту систему. Пример этого таинства находится перед вами - последовательность знаков (букв, пробелов, символов) в совокупности составляет носитель новой (как надеется автор) информации, образующей настоящую книгу.
Еще один удивительный пример - синергетические системы [85]. Здесь вопреки "великому и ужасному" второму закону термодинамики моделировались и наблюдались спонтанные процессы самоорганизации!
Возвращаясь к обсуждению свойств систем, отметим, что важнейшее из них (с точки зрения практического человека) - целенаправленность - наиболее характерно для homo sapiens и связанных с его деятельностью искусственных структур. В отношении природы сказать что-либо однозначное достаточно сложно - есть ли цель у неба? у моря? у погоды (кроме как испортить в Санкт-Петербурге выходной день)? Сам факт наличия закономерностей в природе (законы той же диалектики, законы физики и т.п.) указывает на то, что в принципе какая-то цель (или какие-то цели) вполне может существовать. Эту цель материалисты называют развитием, совмещая результат с процессом его достижения, идеалисты - Божественным промыслом, самопознанием Идеи и т.п. Однако назвать что-либо еще не означает это понять.
В искусственных системах все гораздо понятнее: цель - это результат. Если получен результат, то цель достигнута. Достижение цели, в свою очередь, состоит из решения поставленной задачи (или совокупности задач, образующих проблему). Результат не возникает из ничего, для его достижения всегда необходимо наличие определенных ресурсов. Преобразование ресурса в результат, обеспечивающий достижение цели, осуществляется упорядоченной совокупностью взаимосвязанных действий, образующих операцию. Наличие последнего понятия позволило получить еще одно, вполне прагматическое определение системы [81]: система - это множество взаимосвязанных материальных объектов, непосредственно участвующих в процессе выполнения операции.
Взаимосвязи приведенных понятий можно представить в виде структурной схемы [81], показанной на рис. 3.1.

 
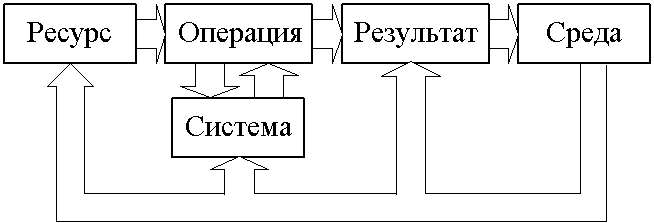
Рис. 3.1. Взаимосвязь основных понятий системного анализа

В научных исследованиях, как правило, приходится иметь дело с так называемыми "сложными", или "большими" системами, рассмотрению которых посвящен следующий параграф. В таких системах особенно подчеркнуто их важнейшее свойство - взаимосвязанность элементов.
В дальнейшем будем различать две основные задачи теории систем: прямую и обратную [128]. Структурные схемы решений указанных задач приведены на рис. 3.2 и 3.3. Прямая задача, или задача анализа, состоит в изучении результатов функционирования системы и определении условий ее применения. Обратная задача, или задача синтеза, связана с определением структуры, параметров и свойств системы в заданном диапазоне возможных условий. При этом предполагается, что в результате синтеза в конечном итоге будет получена система, отвечающая выбранным критериям качества.
Основополагающим этапом понимания любого предмета является классификация. Однако задача классификации систем достаточно сложна в силу крайне высокого уровня общности самого этого понятия. Тем не менее эту работу надо делать: проведение классификации позволяет соискателю сузить диапазон исследований и подобрать наиболее подходящую для данной задачи математическую модель.

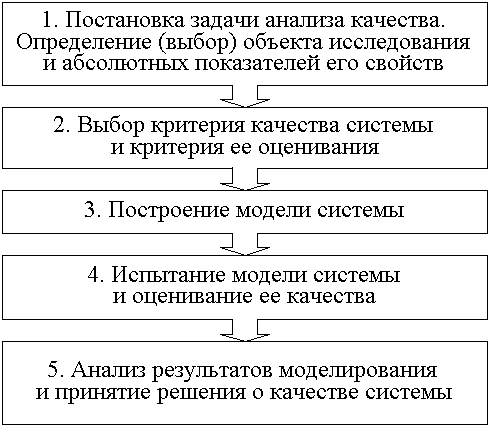
Рис. 3.2. Прямая задача: анализ качества системы

Рис. 3.3. Обратная задача: синтез системы с требуемым качеством
Классификация по свойствам множества  разделяет множество систем в зависимости от характера возможных состояний на дискретные и непрерывные, в зависимости от изменения состояния во времени на статистические  и, как указывалось выше, динамические, в зависимости от степени учета случайных факторов на детерминированные и стохастические. И, наконец, классификация на основе отношения эмерджентности позволяет разделить все системы на регулярные и нерегулярные в зависимости от однозначности отображения множества элементов на множество возможных состояний.
Заметим, что при решении прикладных задач часто используются некоторые установившиеся, общепринятые разбиения систем на составные части. Так, система управления разбивается на управляющую и управляемую подсистемы, а управляющая система - на подсистему наблюдения и собственно управления.

И в заключение этого параграфа приведем диалог Конфуция с учеником, отражающий отношение великого мудреца к системному анализу.
"-Ты считаешь меня многоученым? - спросил Конфуций ученика. - А разве нет? - ответил тот. - Нет, - сказал Конфуций, - я лишь связываю все воедино."

3.2. Сложные системы:
проклятие размерности, декомпозиция

"Эй вы, трое! Оба ко мне! Чего смотришь? Я тебе говорю!"
Известный американский математик профессор Нью-Йоркского университета М. Клайн писал: "Если бы Платон... писал Библию, он, несомненно, начал бы ее такими словами: "Вначале Бог создал математику, а затем небо и звезды согласно законам математики" [64].
В мире царят закономерности, вполне описываемые математическими уравнениями. И люди настолько привыкли к этим закономерностям, что просто не хотят ни замечать их, ни удивляться самому факту их возникновения. Так, например, философские законы диалектики, или законы эволюции разумной цивилизации, представляют собой настоящее чудо, поскольку их генезис (как и происхождение большинства других окружающих нас законов) по сей день остается неясным. Даже для наиболее глубоко изученных физических закономерностей первопричины гравитации, света, электрического тока и других явлений остаются нераскрытыми. Математика в лучшем случае описывает структуру закономерностей, но отнюдь не гарантирует их понимание. Как писал Б.Рассел, "математика представляет собой собрание выводов, которые могут быть применены к чему угодно." Семантика и интерпретация найденных законов требуют их осознания на более высоком уровне - на уровне причин их происхождения и места во всеобщей картине мироздания. Строго говоря, знания современных ученых не так уж далеко ушли вперед в понимании первопричин фундаментальных законов по сравнению со знаниями средневековых схоластов, ссылающихся на Божественный промысел.
Математика - наука очищения, она позволяет обнаружить и идентифицировать закономерности, замаскированные в зашумленных стохастических потоках энергии и информации. Как правило, глубокие, фундаментальные закономерности достаточно просты и допускают красивые аналитические описания. "Наш опыт убеждает нас, - писал А.Эйнштейн, - что природа - это реализация самых простых математических идей." Элегантность осново­полагающих законов оказалась вполне адекватной красоте классической "чистой" математики. Возможно, именно этот факт привел Г.Харди к мысли о том, что "красота есть пробный камень для математической идеи; в мире нет места уродливой математике."
Увы... Стоит только спуститься со снежных вершин ортодоксальной Науки к решению прикладных задач суетного Повседневья, и мы сразу же столкнемся с целым рядом проблем, явно не вписывающихся в изящные формы классических математических моделей. И здесь Ее Величеству Чистой Математике приходится сбросить с себя белоснежную мантию аналитики, засучить рукава и, превратившись в работящую служанку - Прикладную Математику, заняться тяжелым вычислительным трудом - имитационным моделированием, приближенными методами расчета, линеаризацией, обработкой некондиционных статистических данных и т.д. и т.п.
Классической проблемой почти всех прикладных наук является проблема больших, или сложных систем. Как правило, это понятие в каждом конкретном случае уточняется в зависимости от контекста решаемой проблемы. В общем случае под сложной системой понимают многофункциональную систему с многомерной, многосвязной, неоднородной структурой, нестационарно изменяющейся во времени и содержащей существенные неопределенности в описании. Иногда, "для букета", добавляют некорректность задания, недифференцируемость протекающих в ней процессов, ограниченную наблюдаемость, слабую управляемость и т.п.
Можно предложить альтернативное определение: сложная система - это система, не допускающая красивого математического описания.
Вывод из представленного выше определения достаточно очевиден - необходимо по возможности упростить и модель исследуемой системы, и саму решаемую задачу. Соответствующие математические технологии описаны, например, в [53, 78, 80, 91, 112]. Проблема состоит в том, чтобы сделать это корректно!

NB!: Введение корректных ограничений и упрощений, строгое применение техники декомпозиции - задачи, требующие от соискателя особого внимания и предельной аккуратности. Именно здесь возникают серьезные вопросы, а иногда и проблемы при защите диссертационной работы.

Идея декомпозиции достаточно очевидна - разделить изучаемую систему на подсистемы, а решаемую задачу - на подзадачи, каждая из которых допускает более или менее самостоятельное исследование. Если вычлененная подсистема слишком сложна, то продолжают процесс разбиения до тех пор, пока не получат подсистему, допускающую определенное решение. По существу реализуется иерархическая, или многоуровневая структуризация исходной задачи (системы). Для формализованного решения задачи декомпозиции удобно использовать математический аппарат теории графов и технологию структурного программирования.
Как правило, сложная система допускает несколько вариантов декомпозиции, что связано с наличием различных подходов к задаче анализа ее функционирования. В результате возникают неоднозначность, субъективизм выбора, многокритериальность и другие неприятности, существенно затрудняющие получение строгого решения. При этом не последнюю роль приобретают интуиция и опыт исследователя. По данным психологов, человек может мысленно охватить структуру декомпозированной системы, если на каждом уровне возникает не более 5±2 подзадач [53].
Научная методология постановки и решения задач исследования сложных систем получила наименование "системный анализ". По своей природе системный анализ представляет собой некоторое обобщение различных методических приемов, возникающих при решении конкретных естественно-научных, социальных, военных, технических и других задач. Несмотря на содержательную разнородность таких задач, системный анализ позволяет существенно унифицировать технологию их решения. В частности, в работе [53] представлен вариант общей схемы алгоритма решения задачи исследования системы (рис. 3.4).
Следует заметить, что одной из типичных проблем, возникающих при исследовании сложных систем, является так называемое "проклятие размерности" [72]. В соответствии с законами Мэрфи, "задача, имеющая размерность меньше трех, тривиальна, а имеющая размерность больше восьми - не имеет решения."
Очевидной неприятностью, вытекающей из высокой размерности решаемой задачи, является нелинейный рост требований к вычислительным ресурсам используемой ЭВМ. Так, например, объем вычислений, необходимых для реализации алгоритма следящего наблюдателя, растет пропорционально третьей степени от размерности вектора состояния контролируемого объекта.
К сожалению, возникающие в результате роста размерности задачи проблемы не исчерпываются чисто техническими аспектами; в задачах с высокой размерностью возникают многочисленные "таинственные" явления, объяснение которых представляет собой самостоятельную, отнюдь не тривиальную задачу. Как замечено в мэрфологическом принципе Шательера, сложные системы имеют тенденцию противопоставлять себя своим же функциям.
В качестве примера приведем задачи теории наблюдения динамических систем, в которых рост числа контролируемых параметров увеличивает вероятность появления таких переменных, которые слабо зависят от изменений входных переменных (измерений). В результате соответствующая градиентная матрица оказывается вырожденной или плохо обусловленной, что приводит к полной или частичной потере наблюдаемости.
Аналогичные проблемы возникают в задачах управления большеразмерными системами, в задачах прогнозирования, идентификации и т.п. Мэрфологический принцип неопределенности утверждает, что системы имеют тенденцию расти и по мере роста взаиморастворяться. Другие формулировки звучат не менее пессимистично: "Сложные системы приводят к неожиданным последствиям" или "Совокупное поведение больших систем предсказать нельзя".

Рис. 3.4. Вариант общей схемы алгоритма
решения задачи исследования системы

Для борьбы с "проклятьем размерности" используется разнообразный математический аппарат, охватывающий широкий спектр вычислительных технологий от методов агрегирования сложных систем (задача, обратная декомпозиции) [24, 121] до алгоритмов тихоновской или иной регуляризации [113]. Выбор наиболее подходящей технологии в каждом конкретном случае индивидуален и лежит в области системотехнического искусства, приобретаемого долгим и нелегким опытом. Остается надеяться, что если не соискатель, то ходя бы его научный руководитель таким опытом обладает.

ольшие системы - сплошные проблемы, В сомненьях гипотез тоскуют дилеммы, Решенья в тумане, такие дела: Системный анализ не мать родила! Проблема понятна, но как подойти? Сплошные тропинки, но нету пути, И матаппарат, словно Африка, сшит - Одни лоскуточки, а смысл позабыт. И что улучшать? Показателей тьма, Посмотришь на них - заболит голова, Один приподнимешь, другой упадет - Системные связи... такой вот компот! Что лучше? Что хуже? Поди разбери, И с вектором вектор попробуй сравни! А меру введешь, чтобы в скаляр войти, Попробуй потом объективность найти! Ведь меру всегда можно так подобрать, Что лучше систему уже не сыскать, А выигрыша вроде бы вовсе и нет, Бумага все стерпит, пишите, привет! Но есть интегральный критерий, ура! А как его вычислить? - - Вот в чем беда. Трухлявых методик на полках полно, А внутрь заглянешь - все то же зеро! Все те же три "п": палец, пол, потолок, Туман a priori, обычный итог, "И грустно, и скучно," и что здесь сказать, Когда диссертацию надо писать. Ну что ж, остается, забыв про итог, Взять гвозди, пилу и большой молоток, И сделать модель из фанерных листов, Не тратя ни нервы, ни время от снов. Программы напишем в Паскале и в СИ, Ошибки, конечно же, Бог нам простит, И формулу Байеса впишем в трактат, Кто с Байеса сможет спросить результат?! Конечно, система такая не впрок, Ну что же поделать, таков потолок, Мы рациональной ее назовем, И все замечания этим убъем. Напишем введение, долгий обзор И терминов умных таинственный сор Для вкуса добавим. Ну что же еще? Ковать нужно "дело", пока горячо! Ну вот и защита, прочитан доклад, Вопросы, ответы, порой невпопад, Пусть члены Совета ворочают нос: Не понял один, а другой - не дорос! Зато не обидят, и то хорошо, Диплом свое место в кармане нашел, И, став кандидатом мудрейших наук, Адъюнктов возьмем... Замыкается круг!

3.3. Математические модели:
искусство и наука

"Предположим, на горизонте появилось N самолетов противника ... Нет, N - это слишком много, лучше - К."
Математическое моделирование представляет собой сложный симбиоз науки и искусства, предполагающий, с одной стороны, энциклопедическое знание почти всех разделов современной математики, а с другой - тонкое интуитивное восприятие исследуемых процессов и систем.
Теоретические основы математического моделирования находятся в стадии столь высокого абстрагирования и гипертрофированной общности, что почти не допускают извлечения какого-либо конструктивного результата, полезного для практики [42, 68, 78]. Иными словами, "легко из дома реальности зайти в лес математики, но мало кто умеет вернуться назад" [127].
В связи с этим большая часть авторов, старающихся приобщить новые поколения ученых к науке моделирования, предпочитает иной, вполне проторенный путь написания книг. Этот путь представляет собой формирование эклектической смеси неглубоких срезов из различных разделов прикладной математики - дифференциальных уравнений, теории вероятностей, алгебраических, логических или топологических методов и т.п. В качестве примера можно привести книги [77, 83, 105 и др.]. Такого рода литература весьма полезна для развития математической эрудиции и общей ориентации в практике моделирования.
И, наконец, еще один вид литературы, относящейся к математическому моделированию, связан с узко специализированными монографиями, ориентированными на глубокое и конструктивное изучение конкретных типов моделей [71, 92, 98 и др.].
Разработка математической модели, как правило, включает в себя три основных этапа - выбор структуры, определение параметров и проверку подобия. В общем случае моделирование осуществляется итерационно. Это связано с тем, что практически невозможно оценить качество выбранной непараметрической структуры модели без оценки ее параметров.
Априорный выбор структуры, в свою очередь, предполагает наличие у разработчика модели, с одной стороны, глубоких знаний об изучаемом процессе или системе, а с другой - хотя бы общих представлений о существующих в настоящее время математических моделях. Упорядочение таких представлений осуществляется на основе классификаций. В зависимости от выбранного классификационного показателя модели разделяются на статические и динамические, линейные и нелинейные, сосредоточенные и распределенные, дискретные и непрерывные, детерминированные и стохастические и т.п.
Иногда простейшая классификация оказывается не достаточно полной. Так, например, множество моделей, отражающих неопределенность ситуации, можно разделить на стохастические, нечеткие и хаотические [53].
Классификация моделей в основном повторяет классификацию систем. Однако это вовсе не означает, что тип модели должен соответствовать типу моделируемой системы. Так, например, движение любой материальной точки представляет собой непрерывный во времени процесс; в то же время в качестве его модели на практике чаще всего используется дискретная во времени модель, позволяющая выполнять расчеты с учетом специфики используемой цифровой техники.
Осуществив априорный выбор структуры, разработчик модели переходит к определению ее параметров. В случае, когда имеется набор численных данных, полученных в результате наблюдения за функционированием реальной системы-прототипа или ее экспериментального аналога, искомые параметры находятся путем применения алгоритмов обработки указанной информации. В частности, широко используется математический аппарат статистического оценивания [3, 4, 15, 62, 73 и др.].
Последний этап создания модели связан с проверкой ее адекватности, или подобия моделируемой системе. При этом адекватность понимается в крайне узком смысле этого слова, а именно в контексте близости изучаемых свойств системы и аналогичных характеристик модели. Например, при исследовании выходных характеристик системы формируется мера близости между конкретными выходными показателями реальной системы и ее модели.
Очевидно, что данная мера представляет собой реализацию некоторой случайной величины. Определив функцию распределения этой величины, можно найти по соответствующим таблицам математической статистики критические значения выбранной меры, отвечающие a'priori выбранному уровню доверия разработчика модели своему детищу. Если уровень доверия оказывается ниже критического, необходимо перейти либо к первому этапу и скорректировать структуру модели, либо ко второму этапу сбора и обработки экспериментальных данных. И все начинается сначала...

NB!: "Цифры не управляют миром, но они показывают, как управляется мир."

одели, модели, повсюду модели, Любую проблему сжевали и съели Всесильные челюсти - чудо науки, Работают быстро, не ведая муки, Работают четко, в компьютерном ритме, Ответ представляя в двухцветной палитре: Все черное - black, а все белое - white, О'key, very well, no problem, all right! И вроде похоже, и вроде ответ, А красок других, может, вовсе и нет... Одним мир моделей не слишком хорош: Что в них ты положишь - - лишь то и возьмешь.

3.4. Оптимизация - задачи на экстремум

"Значение синуса в военное время может достигать четырех."
Практически любая научная или техническая разработка является оптимальной. Действительно, всякий обоснованный выбор базируется на некоторой системе предпочтений среди множества допустимых альтернатив. При этом сам выбор осуществляется на основе a'priori выбранного критерия. И поскольку предпочтение всегда отдается наилучшей разработке, т.е. той, для которой критериальный показатель качества достигает экстремального значения, можно утверждать, что концепция оптимизации есть математическая основа любого системного синтеза.
В той или иной форме решение задач на экстремум характерно почти для всех научных проблем. Еще Леонард Эйлер утверждал: "В мире не происходит ничего, в чем не был бы виден смысл какого-нибудь максимума или минимума."
Следует сразу оговориться, что безусловных экстремумов в реальных прикладных задачах практически не бывает. Всегда существует набор серьезных ограничений, позволяющий найти лишь условно оптимальное решение. Различного рода ограничениям будет посвящен следующий параграф. Однако это не является основанием уклоняться от оптимизационной методологии и переходить к синтезу некорректных полуэвристических структур (системы, процессы, средства и т.п.) с грубой оценкой их свойств на имитационных моделях. Осознавая некондиционность таких разработок, их авторы дают им различные "самостийные" названия - "рациональная", "типовая" и т.п., что, как правило, не спасает их от вполне справедливой критики.
Математический аппарат оптимизации разработан достаточно широко и глубоко и включает в себя такие крупные разделы современной прикладной математики, как классическое вариационное исчисление, линейное, нелинейное и целочисленное программирование, динамическое программирование и принцип максимума Понтрягина, методы минимакса и многое, многое другое.
Как правило, выбор той или иной целевой (или критериальной) функции достаточно субъективен и опирается на личный опыт исследователя. На основании выбранной целевой функции формируется критерий оптимизации. Методы оптимизации сводятся к нахождению решения, обеспечивающего экстремальное значение выбранного критериального показателя.
Критериальный показатель (показатель качества) может выражать вероятность достижения поставленной перед разрабатываемой системой задачи, помехоустойчивость канала передачи данных, безотказность системы управления и т.п. В этих случаях показатель качества в соответствии с критерием оптимизации нужно максимизировать. В задачах, где определяется вероятность появления ошибки в системе передачи данных, стоимость эксплуатационных расходов и т.п., его необходимо минимизировать.
В статических задачах, где исследуемая система описывается алгебраическими уравнениями, критериальный показатель представляет собой функцию нескольких переменных:

где - некоторая скалярная функция; - вектор параметров.
В подобных случаях задача оптимизации состоит в отыскании экстремумов функции с учетом имеющихся ограничений. Методы решения таких задач рассмотрены, например, в работах по линейному и нелинейному программированию [28, 30, 89 и др.].
В динамических задачах обычно является функционалом, т.е. числом, зависящим от вида функций, определяющих состояние  системы, управляющие  и возмущающие  воздействия, а также интервала времени:

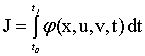(3.2)

где  и – фиксированные значения времени;   –скалярная знакопостоянная функция.
Функционал (3.2) или его частные случаи используются в детерминированных задачах, где все вектор-функции  являются регулярными.
На практике, как правило, вектор-функция возмущений  представляет собой случайную вектор-функцию аргумента . В связи с этим функционал из (3.2) является случайной величиной. Здесь уже невозможно обеспечить наилучшее поведение системы в каждом отдельном процессе. Такие системы должны быть наилучшими в среднем. Тогда, если обозначить через  математическое ожидание, функционал (критериальная функция)  примет вид
.
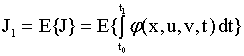Оптимальной системой при рассмотренной постановке задачи будет система, параметры которой обеспечивают минимум (максимум) величины.

 априорной моделью исследуемой задачи.

Правдоподобность и широкая распространенность таких ситуаций была давно замечена учеными, работающими в различных областях науки, и отражена в принципах "мэрфологии" в виде следствий к основополагающему закону Мэрфи [110].
1. Все не так легко, как кажется.
2. Всякая работа требует больше времени, чем Вы думаете.
3. Из всех неприятностей произойдет именно та, ущерб от которой больше.
4. Если четыре причины возможных неприятностей заранее устранены, то всегда найдется пятая.
5. Предоставленные сами себе, события имеют тенденцию развиваться от плохого к еще худшему.
6. Всякое решение плодит новые проблемы.

Особенно актуальна проблема обеспечения устойчивости решения в конфликтных ситуациях, изучаемых в теории игр. Для обеспечения гарантированной устойчивости результатов используется так называемый минимаксный критерий,

позволяющий определить такие параметры системы, при которых обеспечивается наилучший по сравнению с любой другой системой результат в наихудшем (на множестве рассматриваемых ситуаций) случае. Другими словами, наихудший результат в минимаксной системе лучше, чем наихудший результат в любой отличной от неё системе.
В качестве примера минимаксного подхода можно привести задачу минимизации функционала, определяющего вероятность принятия неправильного решения и равного

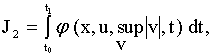
при условии, что вектор возмущающих воздействий  будет достигать наибольших по модулю значений.
Следует заметить, что в конфликтных ситуациях наихудший случай имеет место тогда, когда противная сторона придерживается своей оптимальной стратегии. И еще одно малоприятное замечание: противник, предполагающий использование минимаксной стратегии с противоположной стороны, в целях нанесения наибольшего урона будет опираться не на "оптимальную" стратегию (в контексте исходной постановки задачи), а на какую-то другую, противостоящую минимаксному решению. Отсюда возникают стратегии бесконечных рефлексивных игр, далеко не всегда имеющие корректные сходящиеся решения. И порой наилучшее решение может быть сформировано на основе методики телевизионной игры "Блеф-клуб" ("А верите ли Вы, что..."). Иногда такой подход называют "военным искусством."
Более подробно задача синтеза статистических и минимаксных систем будет рассмотрена в 5-й гл. Книги.

роцесс оптимизации Для строгой диссертации Важнее кислорода - Ведь такова природа Отточенных наук: Создание из мук, Бессонниц и исканий Конструкций новых зданий, В которых эффективность С триумфом превратилась В extremum maximorum , Тогда Совета кворум Без лишнего сомненья Поймет твое решенье И даст "зеленый свет" Для будущих побед!

3.5. Ограничения - реалии жизни

"По команде "отбой" наступает темное время суток."
Можно использовать для решения поставленной диссертационной задачи замечательные оптимизационные или иные методы современной математики и тем не менее получить сугубо негативные результаты. Быстро забываемый классик материализма Ф.Энгельс писал по этому поводу: "Если наши предпосылки верны и если мы правильно применяем к ним законы мышления, то  результат  должен соответствовать действительности... Но, к сожалению, это почти никогда не имеет место или имеет место в совершенно простых ситуациях." Столь же "оптимистично" высказываются апологеты "мэрфологии" [110]: "В любом наборе исходных данных самая надежная величина, не требующая никакой проверки, является ошибочной" (третий закон Финэйгла).
Подобная ситуация очень распространена в практике научных исследований и связана с наличием существенных ограничений, накладываемых как на природу исходных данных, так и на область применения тех или иных методов прикладной математики.
Совокупность ограничений необходимо учитывать при формировании исходных посылок решаемой задачи. Следуя [18], будем называть исходными посылками такие научные положения, которые являются отправными при выполнении исследования - понятия, категории, термины, определения, гипотезы, принципы, правила, допущения, ограничения. Допущения и ограничения относительно исследования в целом образуют рамки исследований, определяемые временными, пространственными, техническими, экономическими или другими параметрами.
Рассмотрим простейшие модели ограничений. Пусть поведение исследуемой системы S описывается векторным операторным уравнением

,

(3.3)

где – оператор, связывающий векторы  и скалярную переменную ; – вектор-функция координат системы; – вектор-функция управляющих воздействий; – вектор-функция возмущений (помех); - скалярная переменная, обычно являющаяся временем.
Ограничения могут накладываться на любые векторные аргументы (3.3); простейшие ограничения имеют вид условий не превышения параметрами системы некоторых предельных значений. Например, может оказаться, что вектор состояния, в силу физической природы системы  не может превзойти некоторые пределы, определяемые ограниченной замкнутой областью n-мерного пространства переменных [128]. Простейшие ограничения имеют вид r-мерного шара
,
r-мерного куба

или r-мерного параллелепипеда

где  и  – некоторые постоянные.
Обозначим эту область через , а любой вектор  будем считать точкой области. Аналогичные ограничения могут накладываться на управления , возмущения  и временные параметры . В зависимости от характера поставленной задачи динамические характеристики векторных функций состояния, управлений и возмущений накладывают дополнительные условия, например, кусочной непрерывности или дифференцируемости.
В более общем случае ограничения могут быть функционалами вида

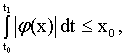
где – некоторая скалярная функция от;  – постоянная величина.
В еще более общем случае ограничивается некоторый функционал от  и  на каком-либо временном интервале . В качестве примера можно привести следующие ограничения:
,

где - некоторые числа; .
Другой тип ограничений связан с наличием априорной (а иногда и апостериорной) неопределенности относительно динамических и статистических характеристик исходных данных. Наличие неопределенности приводит к рассогласованию природы исходных данных и ограничений на корректное применение того или иного математического аппарата, что и дает ошибочные результаты.
Именно об этом писал Т. Гексли: "Как великолепнейшая в мире мельница не доставит нам пшеничной крупчатки из лебеды, так и страницы формул не доставят определенного результата по сомнительным данным."

а каждую свободу есть задвижка. Прекрасен мир в волшебных старых книжках, Но в жизни все, конечно же, не так, И если ты мудрец, а не простак, То ты поймешь Законы Равновесья: Цикличен мир, и жизни этой песня Колеблется в полях Добра и Зла, И даже чаша полная вина Порой чревата болью головною... Ограниченья созданы Судьбою, Они несут свой собственный резон, Срывая формул строгий унисон, И с ними все обязаны считаться, И, как ни трудно, нужно расставаться С гармонией изящных теорем. Реалий жизни будничный пример Не уложить в короткие пределы, Где математик мог бы очень смело Решенье однозначное найти, А это значит, новые пути Торить придется в мире неизвестном... Ну что же, тяжело, зато не пресно, И можно жить без денег не уныло: Ограниченья - движущая сила!

Ваш комментарий о книге
Обратно в раздел Наука