Библиотека
Теология
КонфессииИностранные языкиДругие проекты |
Ваш комментарий о книге Немов Р. Психология. Психодиагностика. кн.3ОГЛАВЛЕНИЕЧасть II. Введение в научное психологическое исследование с элементами математической статистикиГлава 1. Что такое экспериментальная педагогическая психологияКраткое содержание Глава 1. Что такое экспериментальная педагогическая психология Часть II. Введение в научное психологическое исследование
Приведем несколько примеров прикладных экспериментальных психолого-педагогических исследований. ____ Глава 1. Что такое экспериментальная педагогическая психология Часть II. Введение в научное психологическое исследование ____ Глава 1. Что такое экспериментальная педагогическая психология__ Часть II, Введение в научное психологическое исследование Глава 1. Что такое экспериментальная педагогическая психология ______ Часть II. Введение в научное психологическое исследование____ ____ Глава 1. Что такое экспериментальная педагогическая психология__ Часть II. Введение в научное психологическое исследование
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
(Истоки экспериментальной психологии: 17-26. Возникновение экспериментальной психологии: 26-67. Развитие экспериментальной психологии с 1940 по 1960 г.: 85-89. Характер экспериментального метода: 99-102.)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Рис. 71. Структура и иерархия гипотез сложного экспериментального психолого-педагогического исследования
Верхнюю ступень в иерархии обычно занимает общая гипотеза. Она непосредственно вытекает из формулировки проблемы и содержит в себе некоторое утверждение, достоверность
18*
547
Часть II. Введение в научное психологическое исследование
которого предстоит доказать в проводимом эксперименте. За общей гипотезой следуют частные, детализирующие, конкретизирующие и раскрывающие ее содержание. Из частных гипотез, в свою очередь, вытекают рабочие гипотезы, представляющие собой суждения, непосредственно проверяемые в эксперименте.
Например, проводится исследование по проверке методики ускорения умственного развития детей. Попробуем сформулировать и представить в виде некоторой иерархизированнои структуры соответствующие ему гипотезы.
Для общей цели — «ускорение процесса умственного развития детей» — может быть предложена следующая общая гипотеза: «В результате проведенного эксперимента процесс умственного развития детей будет ускорен».
Частной цели — «проверка психолого-педагогических средств ускорения процесса развития» — может соответствовать частная гипотеза: «К ускорению процесса развития детей приведут примененные в эксперименте средства психолого-педагогического воздействия на детей».
Для частной цели — «формулировка выводов и практических рекомендаций» — может быть предложена частная гипотеза: «Внедрение в педагогическую практику выводов и рекомендаций, вытекающих из проведенного эксперимента, должно привести к ускорению умственного развития детей».
Теперь попробуем представить себе возможные рабочие гипотезы этого эксперимента:
Рабочая гипотеза 1: «Применение данного типа задач на занятиях данным учебным предметом должно будет ускорить психологическое развитие у учащихся соответствующих научных понятий».
Рабочая гипотеза 2: «Применение приемов проблемного обучения, в частности таких, как..., должно будет способствовать развитию умения учащихся выяснять причинно-следственные связи и отношения».
Рабочая гипотеза 3: «Введение данного типа задач в содержание учебных занятий на уроках... должно будет ускорить формирование соответствующих научных понятий у учащихся».
Рабочая гипотеза 4: «Применение проверенных в эксперименте приемов проблемного обучения будет способствовать раз-
548
____ Глава 2. Виды научных психолого-педагогических исследований___
витию у учащихся словесно-логического мышления, направленного на выяснение причинно-следственных отношений».
Таким образом, в данном примере будет одна общая, две частные и четыре рабочие гипотезы.
При формулировке рабочих гипотез особенно важно соблюдать логические требования, предъявляемые к определению научных понятий. Прежде всего следует обратить внимание на то, чтобы объем и содержание понятий соответствовали аргументам и фактам, критериям и признакам, которые исследователь намеревается использовать для доказательства состоятельности предложенных им гипотез. Язык, на котором формулируются гипотезы, должен быть конкретен и ясен, не содержать в себе двусмысленностей. Если исследователь все же вынужден будет пользоваться многозначными терминами, в том числе понятиями, взятыми из повседневного, обыденного языка, или новыми, еще достаточно не определившимися в науке, то он обязан их уточнить, перевести на общепринятый язык науки и определить в соответствии с требованиями логики определения понятий.
В этой связи следует напомнить о том, что понятие — это совокупность суждений о наиболее общих и специфических признаках предмета или явления, определяемого при помощи данного понятия. Ядром научного понятия является указание на конкретные, наиболее общие в совокупности специфические признаки данного класса объектов. Определение понятия отнюдь не сводится только к дефиниции, т.е. к словесному и краткому указанию лишь существенных признаков соответствующего класса. Определение понятия представляет собой логическую операцию, посредством которой выясняют объем и конкретное содержание данного понятия.
Изучив сотни и тысячи правильных определений, специалисты-логики установили такие способы определения научных понятий, которые позволяют раскрыть их существенные признаки, не прибегая к подробному перечислению других — второстепенных признаков. Основным из таких приемов является определение понятия через ближайший род и видовое отличие. Это означает, что для каждого подлежащего определению понятия прежде всего необходимо такое, которое включает в себя со-
549
Часть II. Введение в научное психологическое исследование
держание данного понятия как свою часть. В каждый род входит несколько видов, и для того, чтобы выяснить содержание вида, соответствующего определенному понятию, необходимо найти тот специфический, существенный признак, который и отличает данный вид от остальных входящих в выделенный род. Если, например, мы хотим точно определить понятие «мотив поведения», то вначале необходимо найти родовое для него понятие. Им будет понятие «личность». Далее необходимо указать на видовое отличие понятия «мотив поведения» от других составляющих личности, таких, например, как «чувства», «свойства темперамента», «черты личности». От них мотив поведения отличается, в частности, тем, что представляет собой внутреннее побуждение к определенным действиям. Ни черты характера, как таковые, ни свойства темперамента такой непосредственной побудительной силой не обладают. Что касается чувств, то им эта сила отчасти свойственна, но и чувства далеко не всегда побуждают человека к определенным действиям и тем самым отличаются от подлинных мотивов поведения. Теперь мы можем дать следующее определение понятию «мотив поведения»: «Это устойчивая особенность личности человека, побуждающая, направляющая и поддерживающая целенаправленную активность, связанную с достижением определенной цели».
В психолого-педагогических экспериментах в качестве рабочих нередко применяются так называемые операциональные определения понятий. Они заключаются в выделении тех или иных объектов или измерительных процедур, применяя которые по заданным правилам, любой человек может удостовериться в том, что признаки, включаемые в объем и содержание данного понятия, действительно существуют и не являются вымышленными.
Пример операционализации понятия «интеллект»: «Интеллект — это общие умственные способности человека, характеризующие его мышление. Интеллект можно оценить по количеству и качеству теоретических и практических задач, решенных человеком за единицу времени». (Далее для полной операционализации понятия достаточно перечислить соответствующие задачи и установить критерии их решения.)
Имеется шесть основных логических требований к определению понятий:
550
____ Глава 2, Виды научных психолого-педагогических исследований__
Нечеткость в определениях понятий, используемых в гипотезах и в логике доказательства в эксперименте, весьма затрудняет, а иногда делает вообще невозможным выяснение истины. Расплывчатость и нечеткость определений — одна из основных ошибок в понятиях, используемых в экспериментальных психолого-педагогических исследованиях, и это обстоятельство существенно снижает их научную и практическую ценность. Именно по этой причине многие диссертационные и другие исследования, проведенные учеными-педагогами и психологами, не находят выход в практику.
Другими типичными ошибками в определениях понятий являются следующие:
551
Часть II. Введение в научное психологическое исследование
Неполное деление объема понятия — это такое явление, когда при перечислении видовых признаков понятия некоторые из них пропускаются. Слишком обширное деление объема понятия заключается в том, что в объем делимого понятия вводятся некоторые частные признаки, которые сами по себе несущественны или в самом понятии не содержатся. В таком случае общая сумма объемов видовых признаков обычно превышает объем делимого, или определяемого, понятия.
Ошибка перекрестного деления состоит в том, что в процессе деления объема понятия берется несколько разных, не согласующихся друг с другом оснований для деления объема понятия.
Скачок в делении — это ошибка, вызванная нарушением правила непрерывности деления, когда некоторые существенные признаки понятия пропускаются.
Особенно важны формулировки рабочих гипотез, так как именно эти гипотезы непосредственно проверяются в эмпирической части эксперимента. Убедительное доказательство этих гипотез в свою очередь дает основание для утверждения правильности частных и общей гипотезы. Для того чтобы указанная последовательность в логике доказательства гипотез разного уровня была соблюдена, необходимо избегать типичных ошибок в определениях самих рабочих гипотез.
Первая из них состоит в том, что рабочая гипотеза по объему и содержанию входящих в нее понятий может быть утверждением слишком общего типа и из-за этого практически недоказуемой в одном эксперименте. Например, ни в каком частном эксперименте невозможно ни полностью доказать, ни окончательно опровергнуть следующую рабочую гипотезу: «Школа положительно (отрицательно) влияет на ребенка». Во-первых, школы могут быть разными; во-вторых, их влияние может быть различным; в-третьих, разными могут быть и дети, на которых проводится исследование. Как в реальной жизни, так и в экспериментальном исследовании можно будет легко обнаружить немало как частных подтверждений, так и опровержений предложенной гипотезы.
Вторая ошибка состоит в том, что в формулировке гипотезы могут оказаться понятия, неоднозначно трактуемые в самой на-
552
____ Глава 2. Виды научных психолого-педагогических исследований__
уке. Например, экспериментально трудно будет доказать следующее утверждение: «Данная программа обучения является развивающей», так как понятие «развивающая» в научной литературе не имеет единого, общепринятого определения. Если один экспериментатор, предпочитающий одно из определений, докажет, что предложенная им учебная программа является развивающей, то другой тут же сможет его опровергнуть, использовав такое определение понятия «развивающая», которое не соответствует первому. Неточность научного языка ведет к нескончаемым и бесперспективным спорам в науке и порождает трудноустранимые недостатки в экспериментальных доказательствах. Для того чтобы избежать подобного рода ошибок, перед началом исследования необходимо давать рабочие определения всем многозначным понятиям, используемым в формулировках рабочих гипотез. Тогда легко можно будет ограничить область притязаний исследования и возражать оппонентам.
Третья встречающаяся в гипотезах ошибка состоит в том, что в них могут быть включены понятия, вообще не определенные в науке. К примеру, утверждение типа «Воздействуя на экстрасенсорику ученика, можно добиться существенных изменений в его поведении» не может считаться гипотезой научного исследования по той простой причине, что науке до сих пор не известно, что такое «экстрасенсорика», и коль скоро это так, то остается широкое поле для произвола в толковании результатов исследования.
ЛОГИКА ДОКАЗАТЕЛЬСТВА В ПСИХОЛОГО-ПЕДАГОГИЧЕСКОМ ЭКСПЕРИМЕНТЕ
Доказательство экспериментальной гипотезы состоит из трех основных компонентов: фактов, аргументов и демонстрации справедливости предложенной гипотезы, вытекающей из этих аргументов и фактов.
Факты и аргументы, как правило, представляют собой идеи, истинность которых уже проверена или доказана. В силу этого они могут без специального доказательства их справедливости приводиться в обоснование истинности или ложности гипоте-
553
Часть II. Введение в научное психологическое исследование
зы. Демонстрация — это совокупность логических рассуждений, в процессе которых из аргументов и фактов выводится справедливость гипотезы.
Для того чтобы доказательство было убедительным, в нем также необходимо следовать определенным правилам. Одно из них гласит: гипотеза, аргументы и факты должны быть суждениями, ясно и точно определенными. В противном случае оно может быть опровергнуто или подвергнуто сомнению.
Доказываемое положение — в нашем случае гипотеза — на всем протяжении доказательства должно оставаться тождественным, т.е. одним и тем же. Нарушение этого правила обычно ведет к тому, что, несмотря на затраченные усилия, гипотеза остается недоказанной.
Факты и аргументы, приводимые в процессе доказательства - гипотезы, не должны противоречить друг другу, так как это также сводит доказательство на нет. Необходимо строго следить за тем, чтобы соблюдалось следующее правило: аргументы и факты, приводимые в подтверждение гипотезы, сами должны быть истинными и не подлежать сомнению.
Часто встречающаяся ошибка в доказательстве заключается в том, что экспериментально установленная последовательность событий или фактов, их статистически достоверная связь (корреляция) ошибочно принимаются за свидетельство существования причинно-следственной зависимости между этими событиями или фактами. Например, из того, что за некоторым событием А всегда и неизменно следует другое событие Б (скажем, за весной — лето; за положением часовой стрелки на цифре 1 — ее переход на цифру 2), нередко делают вывод о том, что предшествующее событие является причиной наступления последующего (что в приведенных выше примерах, очевидно, неверно). Причинной считается такая зависимость, при которой появление события А не только неизбежно ведет за собой появление события Б, но и само событие Б может явиться лишь тогда, когда до него уже имело место событие А. В двух приведенных выше примерах это не так. Вполне можно представить себе такой случай, что часы остановятся после того, как стрелка окажется на цифре 1, и тогда она не попадет на цифру 2; может случиться экологическая ката-
554
____ Глава 2. Виды научных психолого-педагогических исследований__
строфа, которая сделает климат постоянным, например, превратит его в вечную зиму или в вечное лето, и в этом случае закономерная смена времен года не наступит. В том и в другом примерах подлинные причины последовательного появления событий находятся вне тех событий, которые мы рассматриваем; они-то и придают закономерный характер временной последовательности этих событий.
Ошибки могут иметь место не только в доказательстве, но и в интерпретации связей как причинно-следственных, и для того, чтобы избежать подобных ошибок, рекомендуется организовывать и проводить психолого-педагогический эксперимент в соответствии с одной из заранее продуманных логических схем доказательства, гарантирующих установление именно причинно-следственных зависимостей между изучаемыми переменными.
Основная логическая схема, позволяющая добиться такого результата, довольно простая. Она включает в себя проведение исследования не на одной, а на двух и более группах испытуемых, одна из которых является экспериментальной, а друше — контрольными. При этом экспериментальная группа предназначается для установления достоверных статистических зависимостей между изучаемыми переменными, а контрольные группы — для того, чтобы, сравнивая получаемые в них результаты с теми, которые установлены на экспериментальной группе, отклонять альтернативные причинно-следственному объяснения выявленной статистической зависимости. В простейшем случае реализации этой схемы берутся одна экспериментальная и одна контрольная группы. В экспериментальной группе выделяется и целенаправленно изменяется переменная, которая рассматривается как вероятная причина объясняемого явления, а в контрольной группе ничего этого не происходит. По завершении эксперимента оцениваются и сравниваются между собой изменения, которые в экспериментальной и контрольной группах произошли в другой переменной — зависимой, и если окажется, что в экспериментальной группе эти изменения больше, чем в контрольной, то делается вывод о том, что подлинной их причиной являются именно те вариации независимой переменной, которые имели место в экспериментальной группе.
555
______ Часть II. Введение в научное психологическое исследование____
Существует несколько вариантов практической реализации этой общей схемы. Рассмотрим их.
1. Метод единственного различия. Схематически он представляется следующим образом:
|
В данном случае фиксируется единственное различие между экспериментальной и контрольной группами по признаку Г, которое по завершении эксперимента приводит к появлению единственного различия по признаку Е. На этом основании делается вывод о том, что изменение Г и есть причина замеченных изменений в Е.
2. Метод сопутствующих изменений (обобщенный вариант метода единственного различия).
|
Если, варьируя величину признака Г, мы неизменно получаем изменения только одного признака Е, то Г можно рассматривать в качестве наиболее вероятной причины Е.
3. Метод единственного сходства.
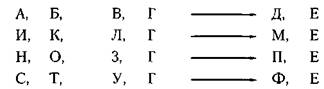
если при разноооразных вариациях признаков неизменным остается единственное сходство (в данном случае: Г—»Е), то составляющие его переменные рассматриваются как причина (Г) и следствие (Е).
Для того, чтобы получаемые в экспериментальной и контрольной группах результаты были сопоставимыми, необходимо, чтобы эти группы по существенным признакам были эквивалентными, т.е. такими, в которых уравнено влияние всех других релевантных переменных, кроме предполагаемой причины.
556
Глава 2. Виды научных психолого-педагогических исследований
Помимо общих логических схем, следование которым в организации и проведении эксперимента помогает выявлению причинно-следственных связей, этой же цели могут служить планы экспериментов. Таких основных планов имеется два:
1. Эксперимент, организованный по плану типа «только после».
В подобного рода исследовании экспериментальные и контрольные группы оцениваются только по окончании эксперимента и не оцениваются в его начале. Если в итоге обнаруживается существенная разница между экспериментальной и контрольной группами, не имевшая место вначале, то можно сделать вывод о том, что отмеченные после эксперимента различия между этими группами были вызваны именно теми экспериментальными действиями, которые предпринимались в отношении экспериментальной группы. Однако в этом случае в качестве альтернативной остается и требует специального опровержения гипотеза о том, что изначально экспериментальная и контрольные группы не были одинаковыми, что и вызвало зафиксированные между ними различия по окончании эксперимента.
2. Эксперимент, организованный по плану типа «до и после».
В данном случае предполагаемые причины и следствия оцениваются и до, и после эксперимента и делается это как в экспериментальной, так и в контрольной группах. Тем самым заранее отбрасывается альтернативная гипотеза о том, что обнаруженные по окончании эксперимента различия между экспериментальной и контрольной группами были вызваны теми различиями между ними, которые имелись еще до начала проведения эксперимента.
Контрольные вопросы
557
Часть II. Введение в научное психологическое исследование
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Фресс П., Пиаже Ж. Экспериментальная психология. Вып. I и II.
М., 1966.
[Формулировка гипотез: 116-120. Эксперимент: 120-148. Наблюдение (как метод экспериментального исследования): 106-115. Обработка и обобщение результатов (эксперимента): 148-193].
Глава 3.
СТАТИСТИЧЕСКИЙ АНАЛИЗ
ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ И СПОСОБЫ
НАГЛЯДНОГО ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ
Краткое содержание
Методы первичной статистической обработки результатов эксперимента. Общее представление о методах статистического анализа экспериментальных данных, назначение этих методов. Деление статистических методов на
558
______ Глава 3. Статистический анализ экспериментальных данных_____
первичные и вторичные. Основные показатели, получаемые в результате первичной обработки экспериментальных данных. Вычисление средней арифметической. Определение дисперсии. Установление примерного распределения данных. Определение моды. Характеристика нормального распределения. Вычисление интервалов.
Методы вторичной статистической обработки результатов эксперимента. Способы вторичной статистической обработки результатов исследования. Регрессионное исчисление. Сравнение средних величин разных выборок. Сравнение частотных распределений данных. Сравнение дисперсий двух выборок. Установление корреляционных зависимостей и их интерпретация. Понятие о факторном анализе как методе статистической обработки.
Способы табличного и графического представления результатов эксперимента. Виды таблиц и их построение. Графическое представление экспериментальных данных. Гистограммы и их применение на практике.
МЕТОДЫ ПЕРВИЧНОЙ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
Методами статистической обработки результатов эксперимента называются математические приемы, формулы, способы количественных расчетов, с помощью которых показатели, получаемые в ходе эксперимента, можно обобщать, приводить в систему, выявляя скрытые в них закономерности. Речь идет о таких закономерностях статистического характера, которые существуют между изучаемыми в эксперименте переменными величинами.
Некоторые из методов математико-статистического анализа позволяют вычислять так называемые элементарные математические статистики, характеризующие выборочное распределение данных, например выборочное среднее, выборочная дисперсия, мода, медиана и ряд других. Иные методы математической статистики, например дисперсионный анализ,регрессионный анализ, позволяют судить о динамике изменения отдельных статистик выборки. С помощью третьей группы методов, скажем, корреляционного анализа, факторного анализа, методов сравнения выборочных данных, можно достоверно судить о статистических связях, существующих между переменными величинами, которые исследуют в данном эксперименте.
559
______ Часть II. Введение в научное психологическое исследование____
Все методы математико-статистического анализа условно делятся на первичные и вторичные1. Первичными называют методы, с помощью которых можно получить показатели, непосредственно отражающие результаты производимых в эксперименте измерений. Соответственно под первичными статистическими показателями имеются в виду те, которые применяются в самих психодиагностических методиках и являются итогом начальной статистической обработки результатов психодиагностики. Вторичными называются методы статистической обработки, с помощью которых на базе первичных данных выявляют скрытые в них статистические закономерности.
К первичным методам статистической обработки относят, например, определение выборочной средней величины, выборочной дисперсии, выборочной моды и выборочной медианы. В число вторичных методов обычно включают корреляционный анализ, регрессионный анализ, методы сравнения первичных статистик у двух или нескольких выборок.
Рассмотрим методы вычисления элементарных математических статистик, начав с выборочного среднего.
Выборочное среднее значение как статистический показатель представляет собой среднюю оценку изучаемого в эксперименте психологического качества. Эта оценка характеризует степень его развития в целом у той группы испытуемых, которая была подвергнута психодиагностическому обследованию. Сравнивая непосредственно средние значения двух или нескольких выборок, мы можем судить об относительной степени развития у людей, составляющих эти выборки, оцениваемого качества.
Выборочное среднее определяется при помощи следующей формулы:
![]()
1 Приводимые здесь определения и высказывания не всегда являются достаточно строгими с точки зрения теории вероятностей и математической статистики как сложившихся областей современной математики. Это сделано для лучшего понимания данного текста студентами, не подготовленными в области математики:
560
______ Глава 3. Статистический анализ экспериментальных данных_____
где х — выборочная средняя величина или среднее арифметическое значение по выборке; п — количество испытуемых в выборке или частных психодиагностических показателей, на основе которых вычисляется средняя величина; хк — частные значения показателей у отдельных испытуемых. Всего таких показателей п, поэтому индекс kданной переменной принимает значения от 1 до п; Е — принятый в математике знак суммирования величин тех переменных, которые находятся справа от этого знака. Выражение X хк соответственно означает сумму всех х с индексом kот
1 до п.
Пример. Допустим, что в результате применения психодиагностической методики для оценки некоторого психологического свойства у десяти испытуемых мы получили следующие частные показатели степени развитости данного свойства у отдельных испытуемых: xi= 5, х2 = 4, х3 = 5, х4 = 6, х5 = 7, *6 = 3, х7 = 6, х& = 2, хд= 8, хт = 4. Следовательно, п = 10, а индекс kменяет свои значения от 1 до 10 в приведенной выше формуле. Для данной выборки среднее значение1, вычисленное по этой формуле, будет равно:
![]()
В психодиагностике и в экспериментальных психолого-педагогических исследованиях среднее, как правило, не вычисляется с точностью, превышающей один знак после запятой, т.е. с большей, чем десятые доли единицы. В психодиагностических обследованиях большая точность расчетов не требуется и не имеет смысла, если принять во внимание приблизительность тех оценок, которые в них получаются, и достаточность таких оценок для производства сравнительно точных расчетов.
Дисперсия как статистическая величина характеризует, насколько частные значения отклоняются от средней величины в данной выборке. Чем больше дисперсия, тем больше отклонения
1 В дальнейшем, как это и принято в математической статистике, с целью сокращения текста мы будем опускать слова «выборочное» и «арифметическое» и просто говорить о «среднем» или «среднем значении».
561
______ Часть II. Введение в научное психологическое исследование____
или разброс данных. Прежде чем представлять формулу для расчетов дисперсии, рассмотрим пример. Воспользуемся теми первичными данными, которые были приведены ранее и на основе которых вычислялась в предыдущем примере средняя величина. Мы видим, что все они разные и отличаются не только друг от друга, но и от средней величины. Меру их общего отличия от средней величины и характеризует дисперсия. Ее определяют для того, чтобы можно было отличать друг от друга величины, имеющие одинаковую среднюю, но разный разброс. Представим себе другую, отличную от предыдущей выборку первичных значений, например такую: 5, 4, 5, 6, 5, 6, 5, 4, 5, 5. Легко убедиться в том, что ее средняя величина также равна 5,0. Но в данной выборке ее отдельные частные значения отличаются от средней гораздо меньше, чем в первой выборке. Выразим степень этого отличия при помощи дисперсии, которая определяется по следующей формуле:
|
где S— выборочная дисперсия, или просто дисперсия;
|
— выражение, означающее, что для всех хк от перво-
го до последнего в данной выборке необходимо вычислить разности между частными и средними значениями, возвести эти разности в квадрат и просуммировать;
п — количество испытуемых в выборке или первичных значений, по которым вычисляется дисперсия.
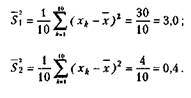 |
562 |
Определим дисперсии для двух приведенных выше выборок частных значений, обозначив эти дисперсии соответственно индексами 1 и 2:'
______ Глава 3, Статистический анализ экспериментальных данных_____
Мы видим, что дисперсия по второй выборке (0,4) значительно меньше дисперсии по первой выборке (3,0). Если бы не было дисперсии, то мы не в состоянии были бы различить данные выборки.
Иногда вместо дисперсии для выявления разброса частных данных относительно средней используют производную от дисперсии величину, называемую выборочное отклонение. Оно равно квадратному корню, извлекаемому из дисперсии, и обозначается тем же
самым знаком, что и дисперсия, только без квадрата— S:
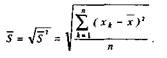
Медианой называется значение изучаемого признака, которое делит выборку, упорядоченную по величине данного признака, пополам. Справа и слева от медианы в упорядоченном ряду остается по одинаковому количеству признаков. Например, для выборки 2, 3, 4, 4, 5, 6, 8, 7, 9 медианой будет значение 5, так как слева и справа от него остается по четыре показателя. Если ряд включает в себя четное число признаков, то медианой будет среднее, взятое как полусумма величин двух центральных значений ряда. Для следующего ряда 0, 1,1, 2, 3, 4, 5, 5, 6, 7 медиана будет равна 3,5.
Знание медианы полезно для того, чтобы установить, является ли распределение частных значений изученного признака симметричным и приближающимся к так называемому нормальному распределению. Средняя и медиана для нормального распределения обычно совпадают или очень мало отличаются друг от друга. Если выборочное распределение признаков нормально, то к нему можно применять методы вторичных статистических расчетов, основанные на нормальном распределении данных. В противном случае этого делать нельзя, так как в расчеты могут вкрасться серьезные ошибки.
Если в книге по математической статистике, где Описывается тот или иной метод статистической обработки, имеются указания на то, что его можно применять только к нормальному или близкому к нему распределению признаков, то необходимо не-
563
______ Часть II. Введение в научное психологическое исследование___
укоснительно следовать этому правилу и полученное эмпирическое распределение признаков проверять на нормальность. Если такого указания нет, то статистика применима к любому распределению признаков. Приблизительно судить о том, является или не является полученное распределение близким к нормальному, можно, построив график распределения данных, похожий на те, которые представлены на рис. 72. Если график оказывается более или менее симметричным, значит, к анализу данных можно применять статистики, предназначенные для нормального распределения. Во всяком случае, допустимая ошибка в расчетах в данном случае будет относительно небольшой.
Приблизительные картины симметричного и несимметричного распределений признаков показаны на рис. 72, где точками miи т2 на горизонтальной оси графика обозначены те величины
признаков, которые соответствуют медианам, а х\ и Х2 — те, которые соответствуют средним значениям.
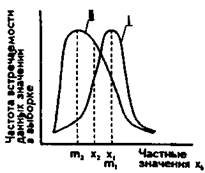 |
Рис. 72. Графики симметричного и несимметричного распределения признаков: I — симметричное распределение (все относящиеся к нему элементарные статистики обозначены с помощью индекса 1); II — несимметричное распределение (его первичные статистики отмечены на графике индексом 2). |
Мода еще одна элементарная математическая статистика и характеристика распределения опытных данных. Модой называют количественное значение исследуемого признака, наиболее часто встречающееся в выборке. На графиках, представленных на рис. 72, моде соответствуют самые верхние точки кривых, вернее, те значения этих точек, которые располагаются на горизонтальной оси. Для симметричных распределений признаков,' в том числе для нормального распределения, значение моды совпадает со значениями среднего и медианы. Для других типов распределений, несимметричных, это не характерно. К примеру, в последовательности значений признаков 1,2, 5,2,4, 2,6,7,2 модой
564
Глава 3. Статистический анализ экспериментальных данных
является значение 2, так как оно встречается чаще других значений — четыре раза.
Иногда исходных частных первичных данных, которые подлежат статистической обработке, бывает довольно много, и они требуют проведения огромного количества элементарных арифметических операций. Для того чтобы сократить их число и вместе с тем сохранить нужную точность расчетов, иногда прибегают к замене исходной выборки частных эмпирических данных на интервалы. Интервалом называется группа упорядоченных по величине значений признака, заменяемая в процессе расчетов средним значением.
Пример. Представим следующий ряд частных признаков: О, 1,1,2,2,3,3,3,4,4,5,5,5,5,6,6,6,7,7,8,8,8,9,9,9,10,10,11,11, 11. Этот ряд включает в себя 30 значений. Разобьем представленный ряд на шесть подгрупп по пять признаков в каждом. Первая подгруппа включит в себя первые пять цифр, вторая — следующие пять и т.д. Вычислим средние значения для каждой из пяти образованных подгрупп чисел. Они соответственно будут равны 1,2; 3,4; 5,2; 6,8; 8,6; 10,6. Таким образом, нам удалось свести исходный ряд, включающий тридцать значений, к ряду, содержащему всего шесть значений и представленному средними величинами. Это и будет интервальный ряд, а проведенная процедура — разделением исходного ряда на интервалы. Теперь все статистические расчеты мы можем производить не с исходным рядом признаков, а с полученным интервальным рядом, и результаты в равной степени будут относиться к исходному ряду. Однако число производимых в ходе расчетов элементарных арифметических операций будет гораздо меньше, чем количество тех операций, которые с этой же целью пришлось бы проделать в отношении исходного ряда признаков. На практике, составляя интервальный ряд, рекомендуется руководствоваться следующим правилом: если в исходном ряду признаков больше чем тридцать, то этот ряд целесообразно разделить на пять-шесть интервалов и в дальнейшем работать только с ними.
Для проверки сказанного проведем пробное вычисление среднего значения по приведенному выше ряду, составляющему тридцать чисел, и по ряду, включающему только интервальные сред-
565
Часть II. Введение в научное психологическое исследование
ние значения. Полученные цифры с точностью до двух знаков после запятой будут соответственно равны 5,97 и 5,97, т.е. являются одинаковыми.
МЕТОДЫ ВТОРИЧНОЙ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
С помощью вторичных методов статистический обработки экспериментальных данных непосредственно проверяются, доказываются или опровергаются гипотезы, связанные с экспериментом. Эти методы, как правило, сложнее, чем методы первичной статистической обработки, и требуют от исследователя хорошей подготовки в области элементарной математики и статистики.
Обсуждаемую группу методов можно разделить на несколько подгрупп: 1. Регрессионное исчисление. 2. Методы сравнения между собой двух или нескольких элементарных статистик (средних, дисперсий и т.п.), относящихся к разным выборкам. 3. Методы установления статистических взаимосвязей между переменными, например их корреляции друг с другом. 4. Методы выявления внутренней статистической структуры эмпирических данных (например, факторный анализ). Рассмотрим каждую из выделенных подгрупп методов вторичной статистической обработки на примерах.
Регрессионное исчисление — это метод математической статистики, позволяющий свести частные, разрозненные данные к некоторому линейному графику, приблизительно отражающему их внутреннюю взаимосвязь, и получить возможность по значению одной из переменных приблизительно оценивать вероятное значение другой переменной.
Воспользуемся для графического представления взаимосвязанных значений двух переменных х и у точками на графике (рис. 73). Поставим перед собой задачу: заменить точки на графике линией прямой регрессии, наилучшим образом представляющей взаимосвязь, существующую между данными переменными. Иными словами, задача заключается в том, чтобы через скопление точек, имеющихся на этом графике, провести прямую линию,
566
|
______ Глава 3. Статистический анализ экспериментальных данных______ |
Рис.73. Прямая регрессии YnoX. х и у — средние значения переменных. Отклонения отдельных значений от линии регрессии обозначены вертикальными пунктирными линиями. Величина yt - у является отклонением измеренного значения переменной у. от оценки, а величина у - у является отклонением оценки от среднего значения (Цит. по: Иберла К. Факторный анализ. М., 1980. С. 23).
пользуясь которой по значению одной из переменных, х или у, можно приблизительно судить о значении другой переменной. Для того чтобы решить эту задачу, необходимо правильно найти коэффициенты а и Ь в уравнении искомой прямой:
у = ах + Ь.
Это уравнение представляет прямую на графике и называется уравнением прямой регрессии.
567 |
Формулы для подсчета коэффициентов а и Ь являются следующими:
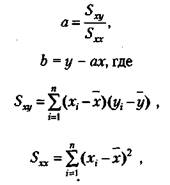
Часть II. Введение в научное психологическое исследование
где х., у{ — частные значения переменных Xи Y, которым соответствуют точки на графике;
х, у — средние значения тех же самых переменных;
п — число первичных значений или точек на графике.
Для сравнения выборочных средних величин, принадлежащих к двум совокупностям данных, и для решения вопроса о том, отличаются ли средние значения статистически достоверно друг от друга, нередко используют ^-критерий Стъюдента. Его основная формула выглядит следующим образом:
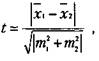
где х{ — среднее значение переменной по одной выборке данных;
хг — среднее значение переменной по другой выборке данных;
т1ит2 — интегрированные показатели отклонений частных значений из двух сравниваемых выборок от соответствующих им средних величин.
/и, и т2 в свою очередь вычисляются по следующим формулам:
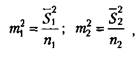
—2
где St— выборочная дисперсия первой переменной (по первой выборке);
—2
5"г — выборочная дисперсия второй переменной (по второй выборке);
я, — число частных значений переменной в первой выборке;
п2 — число частных значений переменной по второй выборке.
После того как при помощи приведенной выше формулы вычислен показатель t, по таблице 32 для заданного числа степеней свободы, равного п{ + п2 - 2, и избранной вероятности допустимой ошибки1 находят нужное табличное значение tи сравнива-
1 Степени свободы и вероятность допустимой ошибки — специальные ма-тематико-статистические термины, содержание которых мы здесь не будем рассматривать.
568
Глава 3. Статистический анализ экспериментальных данных
Таблица 32 Критические значения ^-критерия Стъюдента для заданного числа степеней свободы и вероятностей допустимых ошибок, равных 0,05; 0,01 и 0,001
Число степеней свободы |
Вероятность допустимой ошибки |
||
0,05 0,01 0,001 |
|||
Критические значения показателя t |
|||
(я, + п., - 2) |
|
||
4 |
2,78 |
5,60 |
8,61 |
5 |
2,58 |
4,03 |
6,87 |
6 |
2,45 |
3,71 |
5,96 |
7 |
2,37 |
3,50 |
5,41 |
8 |
2,31 |
3,36 |
5,04 |
9 |
2,26 |
3,25 |
4,78 |
10 |
2,23 |
3,17 |
4,59 |
11 |
2,20 |
3,11 |
4,44' |
12 |
2,18 |
3,05 |
4,32 |
13 |
2,16 |
3,01 |
4,22 |
14 |
2,14 |
2,98 |
4,14 |
15 |
2,13 |
2,96 |
4,07 |
16 |
2,12 |
2,92 |
4,02 |
17 |
2,11 |
2,90 |
3,97 |
18 |
2,10 |
2,88 |
3,92 |
19 |
2,09 |
2,86 |
3,88 |
20 |
2,09 |
2,85 |
3,85 |
21 |
2,08 |
2,83 |
3,82 |
22 |
2,07 |
2,82 |
3,79 |
23 |
2,07 |
2,81 |
3,77 |
24 |
2,06 |
2,80 |
3,75 |
25 |
2,06 |
2,79 |
3,73 |
26 |
2,06 |
2,78 |
3,71 |
27 |
2,05 |
2,77 |
3,69 |
28 |
2,05 |
2,76 |
3,67 |
29 |
2,05 |
2,76 |
3,66 |
30 |
2,04 |
2,75 |
3,65 |
40 |
2,02 |
2,70 |
3,55 |
50 |
2,01 |
2,68 |
3,50 |
60 |
2,00 |
2,66 |
3,46 |
80 |
1,99 |
2,64 |
3,42 |
100 |
1,98 |
2,63 |
3,39 |
ют с ними вычисленное значение t. Если вычисленное значение tбольше или равно табличному, то делают вывод о том, что сравниваемые средние значения из двух выборок действительно ста-
569
______ Часть II. Введение в, научное психологическое исследование___
тистически достоверно различаются с вероятностью допустимой ошибки, меньшей или равной избранной. Рассмотрим процедуру вычисления t-критерия Стъюдента и определения на его основе разницы в средних величинах на конкретном примере.
Допустим, что имеются следующие две выборки экспериментальных данных: 2, 4, 5, 3, 2, 1, 3, 2, 6, 4 и 4, 5, 6, 4, 4, 3, 5, 2, 2, 7. Средние значения по этим двум выборкам соответственно равны 3,2 и 4,2. Кажется, что они существенно друг от друга отличаются. Но так ли это и насколько статистически достоверны эти различия? На данный вопрос может точно ответить только статистический анализ с использованием описанного статистического критерия. Воспользуемся этим критерием.
Поставим найденные значения дисперсий в формулу для подсчета matк вычислим показатель t |
|
Определим сначала выборочные дисперсии для двух сравниваемых выборок значений:
Сравним его значение с табличным для числа степеней свободы 10+10-2 = 18. Зададим вероятность допустимой ошибки, равной 0,05, и убедимся в том, что для данного числа степеней свободы и заданной вероятности допустимой ошибки значение tдолжно быть не меньше чем 2,10. У нас же этот показатель оказался равным 1,47, т.е. меньше табличного. Следовательно, гипотеза о том, что выборочные средние, равные в нашем случае 3,2 и 4,2, статистически достоверно отличаются друг от друга, не подтвердилась, хотя на первый взгляд казалось, что такие различия существуют.
Вероятность допустимой ошибки, равная и меньшая чем 0,05, считается достаточной для научно убедительных выводов. Чем меньше эта вероятность, тем точнее и убедительнее делаемые выводы. Например, избрав вероятность допустимой ошибки, рав-
ную 0,05, мы обеспечиваем точность расчетов 95% и допускаем ошибку, не превышающую 5%, а выбор вероятности допустимой ошибки 0,001 гарантирует точность расчетов, превышающую 99,99%, или ошибку, меньшую чем 0,01%.
Описанная методика сравнения средних величин по критерию Стъюдента в практике применяется тогда, когда необходимо, например, установить, удался или не удался эксперимент, оказал или не оказал он влияние на уровень развития того психологического качества, для изменения которого предназначался. Допустим, что в некотором учебном заведении вводится новая экспериментальная программа или методика обучения, рассчитанная на то, чтобы улучшить знания учащихся, повысить уровень их интеллектуального развития. В этом случае выясняется причинно-следственная связь между независимой переменной — программой или методикой и зависимой переменной — знаниями или уровнем интеллектуального развития. Соответствующая гипотеза гласит: «Введение новой учебной программы или методики обучения должно будет существенно улучшить знания или повысить уровень интеллектуального развития учащихся».
Предположим, что данный эксперимент проводится по схеме, предполагающей оценки зависимой переменной в начале и в конце эксперимента. Получив такие оценки и вычислив средние по всей изученной выборке испытуемых, мы можем воспользоваться критерием Стъюдента для точного установления наличия или отсутствия статистически достоверных различий между средними до и после эксперимента. Если окажется, что они действительно достоверно различаются, то можно будет сделать определенный вывод о том, что эксперимент удался. В противном случае нет убедительных оснований для такого вывода даже в том случае, если сами средние величины в начале и в конце эксперимента по своим абсолютным значениям различны.
Иногда в процессе проведения эксперимента возникает специальная задача сравнения не абсолютных средних значений некоторых величин до и после эксперимента, а частотных, например процентных, распределений данных. Допустим, что для экспериментального исследования была взята выборка из 100 уча-
571
______ Часть II. Введение в научное психологическое исследование____
щихся и с ними проведен формирующий эксперимент. Предположим также, что до эксперимента 30 человек успевали на «удовлетворительно», 30 — на «хорошо», а остальные 40 — на «отлично». После эксперимента ситуация изменилась. Теперь на «удовлетворительно» успевают только 10 учащихся, на «хорошо» — 45 учащихся и на «отлично» — остальные 45 учащихся. Можно ли, опираясь на эти данные, утверждать, что формирующий эксперимент, направленный на улучшение успеваемости, удался? Для ответа на данный вопрос можно воспользоваться статистикой, называемой х2-критерий («хи-квадрат критерий»). Его формула выглядит следующим образом:
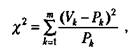
где Рк — частоты результатов наблюдений до эксперимента;
Vk— частоты результатов наблюдений, сделанных после эксперимента;
т — общее число групп, на которые разделились результаты наблюдений.
Воспользуемся приведенным выше примером для того, чтобы показать, как работает хи-квадрат критерий. В данном примере переменная Рк принимает следующие значения: 30%, 30%, 40%, а переменная Vk— такие значения: 10%, 45%, 45%.
Подставим все эти значения в формулу для %2 и определим его величину:
![]()
Воспользуемся теперь таблицей 33, где для заданного числа степеней свободы можно выяснить степень значимости образовавшихся различий до и после эксперимента в распределении оценок. Полученное нами значение х2 = 21,5 больше соответствующего табличного значения т - 1 = 2 степеней свободы, составляющего 13,82 при вероятности допустимой ошибки меньше чем 0,001. Следовательно, гипотеза о значимых изменениях, которые произошли в оценках учащихся в результате введения новой программы или новой методики обучения, эксперимен-
572
Глава 3, Статистический анализ экспериментальных данных_____
Таблица 33 Граничные (критические) значения х2-критерия, соответствующие разным вероятностям допустимой ошибки и разным степеням свободы
Число |
|
|
|
степеней свободы |
Вероятность допустимой ошибки |
||
|
|
|
|
(т-1) |
0,05 |
0,01 |
0,001 |
1 |
3,84 |
6,64 |
10,83 |
2 |
5,99 |
9,21 |
13,82 |
3 |
7,81 |
11,34 |
16,27 |
4 |
9,49 |
13,28 |
18,46 |
5 |
11,07 |
15,09 |
20,52 |
6 |
12,59 |
16,81 |
22,46 |
7 |
14,07 |
18,48 |
24,32 |
8 |
15,51 |
20,09 |
26,12 |
9 |
16,92 |
21,67 |
27,88 |
10 |
18,31 |
23,21 |
29,59 |
11 |
19,68 |
24,72 |
31,26 |
12 |
21,03 |
26,05 |
32,91 |
13 |
22,36 |
27,69 |
34,53 |
14 |
23,68 |
29,14 |
36,12 |
15 |
25,00 |
30,58 |
37,70 |
тально подтвердилась: успеваемость значительно улучшилась, и это мы можем утверждать, допуская ошибку, не превышающую 0,001%.
Иногда в психолого-педагогическом эксперименте возникает необходимость сравнить дисперсии двух выборок для того, чтобы решить, различаются ли эти дисперсии между собой. Допустим, что проводится эксперимент, в котором проверяется гипотеза о том, что одна из двух предлагаемых программ или методик обучения обеспечивает одинаково успешное усвоение знаний учащимися с разными способностями, а другая программа или методика этим свойством не обладает. Демонстрацией справедливости такой гипотезы было бы доказательство того, что индивидуальный разброс оценок учащихся по одной программе или методике больше (или меньше), чем индивидуальный разброс оценок по другой программе или методике.
573
______ Часть II. Введение в научное психологическое исследование____
Подобного рода задачи решаются, в частности, при помощи критерия Фишера. Его формула выглядит следующим образом:
![]()
где п1 —¦ количество значения признака в первой из сравниваемых выборок; п2 — количество значений признака во второй из сравниваемых выборок; {п1 — 1, п2 — 1) — число степеней свободы; 5f — дисперсия по первой выборке; Si— дисперсия по второй выборке.
Вычисленное с помощью этой формулы значение F-крите-рия сравнивается с табличным (табл. 34), и если оно превосходит табличное для избранной вероятности допустимой ошибки и заданного числа степеней свободы, то делается вывод о том, что гипотеза о различиях в дисперсиях подтверждается. В противоположном случае такая гипотеза отвергается и дисперсии считаются одинаковыми1.
Таблица 34
Граничные значения F-критерия для вероятности допустимой ошибки 0,05 и числа степеней свободы и, и и2
я, \. |
3 |
4 |
5 |
6 |
8 |
12 |
16 |
24 |
50 |
3 |
9,28 |
9,91 |
9,01 |
8,94 |
8,84 |
8,74 |
8,69 |
8,64 |
8,58 |
4 |
6,59 |
6,39 |
6,26 |
6,16 |
6,04 |
5,91 |
5,84 |
5,77 |
5,70 |
5 |
5,41 |
5,19 |
5,05 |
4,95 |
4,82 |
4,68 |
4,60 |
4,58 |
4,44 |
6 |
4,76 |
4,53 |
4,39 |
4,28 |
4,15 |
4,00 |
3,92 |
3,84 |
3,75 |
8 |
4,07 |
3,84 |
3,69 |
3,58 |
3,44 |
3,28 |
3,20 |
3,12 |
3,03 |
12 |
3,49 |
3,26 |
3,11 |
3,00 |
2,85 |
2,69 |
2,60 |
2,50 |
2,40 |
16 |
3.-24 |
3,0 |
2,85 |
2,74 |
2,59 |
2,42 |
2,33 |
2,24 |
2,13 |
24 |
3,01 |
2,78 |
2,62 |
2,51 |
2,36 |
2,18 |
2,09 |
1,98 |
1,86 |
50 |
2,79 |
2,56 |
2,40 |
2,29 |
2,13 |
1,95 |
1,85 |
1,74 |
1,60 |
1 Если отношение выборочных дисперсий в формуле F-критерия оказывается меньше единицы, то числитель и знаменатель в этой формуле меняют местами и вновь определяют значения критерия.
574
Глава 3. Статистический анализ экспериментальных данных
Примечание. Таблица для граничных значений ^распределения приведена в сокращенном виде. Полностью ее можно найти в справочниках по математической статистике, в частности в тех, которые даны в списке дополнительной литературы к этой главе.
Пример. Сравним дисперсии следующих двух рядов цифр с целью определения статистически достоверных различий между ними. Первый ряд: 4,6, 5,7,3,4,5,6. Второй ряд: 2,7, 3,6,1,8, 4, 5. Средние значения для двух этих рядов соответственно равны: 5,0 и 4,5. Их дисперсии составляют: 1,5 и 5,25. Частное от деления большей дисперсии на меньшую равно 3,5. Это и есть искомый показатель F. Сравнивая его с табличным граничным значением 3,44, приходим к выводу о том, что дисперсии двух сопоставляемых выборок действительно отличаются друг от друга на уровне значимости более 95% или с вероятностью допустимой ошибки не более 0,05%.
Следующий метод вторичной статистической обработки, посредством которого выясняется связь или прямая зависимость между двумя рядами экспериментальных данных, носит название метод корреляций. Он показывает, каким образом одно явление влияет на другое или связано с ним в своей динамике. Подобного рода зависимости существуют, к примеру, между величинами, находящимися в причинно-следственных связях друг с другом. Если выясняется, что два явления статистически достоверно коррелируют друг с другом и если при этом есть уверенность в том, что одно из них может выступать в качестве причины другого явления, то отсюда определенно следует вывод о наличии между ними причинно-следственной зависимости.
Имеется несколько разновидностей данного метода: линейный, ранговый, парный и множественный. Линейный корреляционный анализ позволяет устанавливать прямые связи между переменными величинами по их абсолютным значениям. Эти связи графически выражаются прямой линией, отсюда название «линейный». Ранговая корреляция определяет зависимость не между абсолютными значениями переменных, а между порядковыми местами, или рангами, занимаемыми ими в упорядоченном по величине ряду. Парный корреляционный анализ включает изучение корреляционных зависимостей только между па-
575
Часть II. Введение в научное психологическое исследование
рами переменных, а множественный, или многомерный, — между многими переменными одновременно. Распространенной в прикладной статистике формой многомерного корреляционного анализа является факторный анализ.
На рис. 74 в виде множества точек представлены различные виды зависимостей между двумя переменными Xи Y(различные поля корреляций между ними).
На фрагменте рис. 74, отмеченном буквой А, точки случайным образом разбросаны по координатной плоскости. Здесь по величине Xнельзя делать какие-либо определенные выводы о величине У. Если в данном случае подсчитать коэффициент корреляции, то он будет равен 0, что свидетельствует о том, что достоверная связь между Xи У отсутствует (она может отсутствовать и тогда, когда коэффициент корреляции не равен 0, но близок к нему по величине). На фрагменте Б рисунка все точки лежат на одной прямой, и каждому отдельному значению переменной Xможно поставить в соответствие одно и только одно значение переменной У, причем, чем большее, тем больше Y. Такая связь между переменными Xи У называется прямой, и если это прямая, соответствующая уравнению регрессии, то связанный с ней коэффициент корреляции будет равен +1. (Заметим, что в жизни такие случаи практически не встречаются; коэффициент корреляции почти никогда не достигает величины единицы.)
На фрагменте В рисунка коэффициент корреляции также будет равен единице, но с отрицательным знаком: -1. Это означает обратную зависимость между переменными Xи У, т.е., чем больше одна из них, тем меньше другая.
На фрагменте Г рисунка точки также разбросаны не случайно, они имеют тенденцию группироваться в определенном направлении. Это направление приближенно может быть представлено уравнением прямой регрессии. Такая же особенность, но с противоположным знаком, характерна для фрагмента Д. Соответствующие этим двум фрагментам коэффициенты корреляции приблизительно будут равны +0,50 и -0,30. Заметим, что крутизна графика, или линии регрессии, не оказывает влияния на величину коэффициента корреляции.
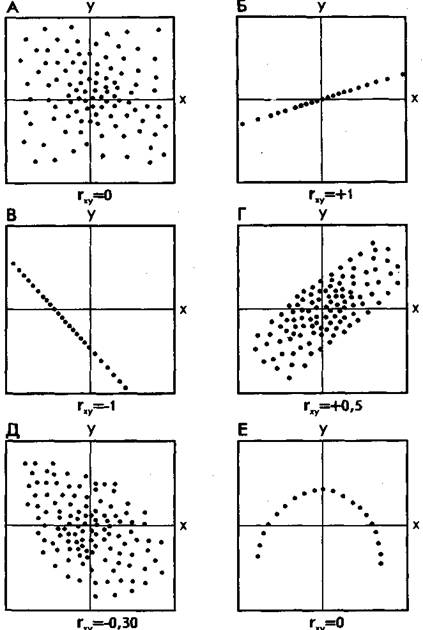
Рис. 74. Схематическое представление различных корреляционных зависимостей с соответствующими значениями коэффициента линейной корреляции (цит. по: Шерла К. Факторный анализ. М, 1980).
577
______ Часть II. Введение в научное психологическое исследование____
Наконец, фрагмент Е дает коэффициент корреляции, равный или близкий к 0, так как в данном случае связь между переменными хотя и существует, но не является линейной.
Коэффициент линейной корреляции определяется при помощи следующей формулы:
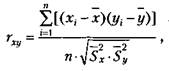
где г — коэффициент линейной корреляции;
х, у — средние выборочные значения сравниваемых величин; х., у — частные выборочные значения сравниваемых величин; п — общее число величин в сравниваемых рядах показателей;
si' Sy~ дисперсии, отклонения сравниваемых величин от
средних значений.
Пример. Определим коэффициент линейной корреляции между следующими двумя рядами показателей. Ряд 1:2,4,4,5,3, 6, 8. Ряд II: 2, 5, 4, 6, 2, 5, 7. Средние значения этих двух рядов соответственно равны 4,6 и 4,4. Их дисперсии составляют следующие величины: 3,4 и 3,1. Подставив эти данные в приведенную выше формулу коэффициента линейной корреляции, получим следующий результат: 0,92. Следовательно, между рядами данных существует значимая связь, причем довольно явно выраженная, так как коэффициент корреляции близок к единице. Действительно, взглянув на эти ряды цифр, мы обнаруживаем, что большей цифре в одном ряду соответствует большая цифра в другом ряду и, наоборот, меньшей цифре в одном ряду соответствует примерно такая же малая цифра в другом ряду.
К коэффициенту ранговой корреляции в психолого-педагогических исследованиях обращаются в том случае, когда признаки, между которыми устанавливается зависимость, являются качественно различными и не могут быть достаточно точно оценены при помощи так называемой интервальной измерительной шкалы. Интервальной называют такую шкалу, которая позволяет оценивать расстояния между ее значениями и судить о
578
______ Глава 3. Статистический анализ экспериментальных данных_____
том, какое из них больше и насколько больше другого. Например, линейка, с помощью которой оцениваются и сравниваются длины объектов, является интервальной шкалой, так как, пользуясь ею, мы можем утверждать, что расстояние между двумя и шестью сантиметрами в два раза больше, чем расстояние между шестью и восемью сантиметрами. Если же, пользуясь некоторым измерительным инструментом, мы можем только утверждать, что одни показатели больше других, но не в состоянии сказать на сколько, то такой измерительный инструмент называется не интервальным, а порядковым.
Большинство показателей, которые получают в психолого-педагогических исследованиях, относятся к порядковым, а не к интервальным шкалам (например, оценки типа «да», «нет», «скорее нет, чем да» и другие, которые можно переводить в баллы), поэтому коэффициент линейной корреляции к ним неприменим. В этом случае обращаются к использованию коэффициента ранговой корреляции, формула которого следующая:
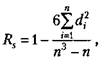
где Rs— коэффициент ранговой корреляции по Спирмену;
di— разница между рангами показателей одних и тех же испытуемых в упорядоченных рядах;
п — число испытуемых или цифровых данных (рангов) в коррелируемых рядах.
Пример. Допустим, что педагога-экспериментатора интересует, влияет ли интерес учащихся к учебному предмету на их успеваемость. Предположим, что с помощью некоторой психодиагностической методики удалось измерить величину интереса к учению и выразить его для десяти учащихся в следующих цифрах: 5,6,7,8,2,4,8,7,2,9. Допустим также, что при помощи другой методики были определены средние оценки этих же учащихся по данному предмету, оказавшиеся соответственно равными: 3,2; 4,0; 4,1; 4,2; 2,5; 5,0; 3,0; 4,8; 4,6; 2,4.
Упорядочим оба ряда оценок по величине цифр и припишем каждому из учащихся по два ранга; один из них указывает на то,
19* 579
______ Часть II. Введение в научное психологическое исследование____
какое место среди остальных данных ученик занимает по успеваемости, а другой — на то, какое место среди них же он занимает по интересу к учебному предмету. Ниже приведены ряды цифр, два из которых (первый и третий) представляют исходные данные, а два других (второй и четвертый) — соответствующие ранги1:
2-1,5 |
2,4-1 |
2-1,5 |
2,5-2 |
4-3 |
3,0-3 |
5-4 |
3,2 - 4 |
6-5 |
4,0-5 |
7-6,5 |
4,1-6 |
7-6,5 |
4,2-7 |
8-8,5 |
4,6-8 |
9-10 |
5,0 - 10 |
Определив сумму квадратов различий в рангах ( ^df) и подставив нужное значение в числитель формулы, получаем, что коэффициент ранговой корреляции равен 0,97, т.е. достаточно высок, что и говорит о том, что между интересом к учебному предмету и успеваемостью учащихся действительно существует статистически достоверная зависимость.
Однако по абсолютным значениям коэффициентов корреляции не всегда можно делать однозначные выводы о том, являются ли они значимыми, т.е. достоверно свидетельствуют о существовании зависимости между сравниваемыми переменными. Может случиться так, что коэффициент корреляции, равный 0,50, не будет достоверным, а коэффициент корреляции, составивший 0,30, — достоверным. Многое в решении этого вопроса зависит от того, сколько показателей было в коррелируемых друг с другом рядах признаков: чем больше таких показателей, тем меньшим по величине может быть статистически достоверный коэффициент корреляции.
В табл. 35 представлены критические значения коэффициентов корреляции для различных степеней свободы. (В данном
1 Если исходные данные, которые ранжируются, одинаковы, то и их ранги также будут одинаковыми. Они получаются путем суммирования и деления пополам тех рангов, которые соответствуют этим данным.
580
Глава 3. Статистический анализ экспериментальных данных_____
Таблица 35 Критические значения коэффициентов корреляции для различных степеней свободы (и - 2) и разных вероятностей допустимых ошибок
Число |
|
|
|
степеней свободы |
Уровень значимости |
[ |
|
0,05 |
0,01 |
0,001 |
|
2 |
0,9500 |
0,9900 |
0,9900 |
3 |
8783 |
9587 |
9911 |
4 |
8114 |
9172 |
9741 |
5 |
0,7545 |
0,8745 |
0,9509 |
6 |
7067 |
8343 |
9249 |
7 |
6664 |
7977 |
8983 |
8 |
6319 |
7646 |
8721 |
9 |
6021 |
7348 |
8471 |
10 |
0,5760 |
0,7079 |
0,8233 |
И |
5529 |
6833 |
8010 |
12 |
5324 |
6614 |
7800 |
13 |
5139 |
6411 |
7604 |
14 |
4973 |
6226 |
7419 |
15 |
0,4821 |
0,6055 |
0,7247 |
16 |
4683 |
5897 |
7084 |
17 |
4555 |
5751 |
6932 |
18 |
4438 |
5614 |
6788 |
19 |
4329 |
5487 |
6625 |
20 |
0,4227 |
0,5368 |
0,6524 |
21 |
4132 |
5256 |
6402 |
22 |
4044 |
5151 |
6287 |
23 |
3961 |
5052 |
6177 |
24 |
3882 |
4958 |
6073 |
25 |
0,3809 |
0,4869 |
0,5974 |
26 |
3739 |
4785 |
5880 |
27 |
3673 |
4705 |
5790 |
28 , |
3610 |
4629 |
5703 |
29 |
3550 |
4556 |
5620 |
30 |
0,3494 |
0,4487 |
0,5541 |
31 |
3440 |
4421 |
5465 |
32 |
3388 |
4357 |
5392 |
33 |
0,3338 |
0,4297 |
0,5322 |
34 |
3291 |
4238 |
5255 |
35 |
0,3246 |
0,4182 |
0,5189 |
36 |
3202 |
4128 |
5126 |
37 |
3160 |
4076 |
5066 |
38 |
3120 |
4026 |
5007 |
39 |
3081 |
3978 |
4951 |
40 |
0,3044 |
0,3932 |
0,4896 |
случае степенью свободы будет число, равное и — 2, где п — количество данных в коррелируемых рядах.) Заметим, что значимость коэффициента корреляции зависит и от заданного уровня значимости или принятой вероятности допустимой ошибки в расчетах. Если, к примеру, коррелируется друг с другом два ряда цифр по 10 единиц в каждом и получен коэффициент корреляции между ними, равный 0,65, то он будет значимым на уровне 0,95 (он больше критического табличного значения, составляющего 0,6319 для вероятности допустимой ошибки 0,05, и меньше критического значения 0,7646 для вероятности допустимой ошибки 0,01).
Метод множественных корреляций в отличие от метода парных корреляций позволяет выявить общую структуру корреляционных зависимостей, существующих внутри многомерного экспериментального материала, включающего более двух переменных, и представить эти корреляционные зависимости в виде некоторой системы.
Один из наиболее распространенных вариантов этого метода — факторный анализ — позволяет определить совокупность внутренних взаимосвязей, возможных причинно-следственных связей, существующих в экспериментальном материале. В результате факторного анализа обнаруживаются так называемые факторы — причины, объясняющие множество частных (парных) корреляционных зависимостей.
Фактор — математико-статистическое понятие. Будучи переведенным на язык психологии (эта процедура называется содержательной или психологической интерпретацией факторов), он становится психологическим понятием. Например, в известном 16-факторном личностном тесте Р. Кеттела, который подробно рассматривался в первой части книги, каждый фактор взаимно однозначно связан с определенными чертами личности человека.
С помощью выявленных факторов объясняют взаимозави-. симость психологических явлений. Поясним сказанное на примере. Допустим, что в некотором психолого-педагогическом эксперименте изучалось взаимовлияние таких переменных, как характер, способности, потребности и успеваемость учащихся. Предположим далее, что, оценив каждую из этих переменных у
582
Глава 3. Статистический анализ экспериментальных данных
достаточно представительной выборки испытуемых и подсчитав коэффициенты парных корреляций между всевозможными парами данных переменных, мы получили следующую матрицу интеркорреляций (в ней справа и сверху цифрами обозначены в перечисленном выше порядке изученные в эксперименте переменные, а внутри самого квадрата показаны их корреляции друг с другом; поскольку всевозможных пар в данном случае меньше, чем клеток в матрице, то заполнена только верхняя часть матрицы, расположенная выше ее главной диагонали).
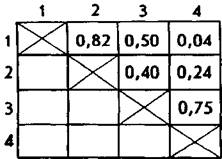 |
Анализ корреляционной матрицы показывает, что переменная 1 (характер) значимо коррелирует с переменными 2 и 3 (способности и потребности). Переменная 2 (способности) достоверно коррелирует с переменной 3 (потребности), а переменная 3 (потребности) — с переменной 4 (успеваемость). Фактически из шести имеющихся в матрице коэффициентов корреляции четыре являются достаточно высокими и, если предположить, что они определялись на совокупности испытуемых, превышающей 10 человек, — значимыми.
Зададим некоторое правило умножения столбцов цифр на строки матрицы: каждая цифра столбца последовательно умножается на каждую цифру строки и результаты парных произведений записываются в строку аналогичной матрицы. Пример: если по этому правилу умножить друг на друга три цифры столбца и строки, представленные в левой части матричного равенства, то получим матрицу, находящуюся в правой части этого же равенства:
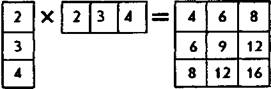
583
Часть II. Введение в научное психологическое исследование
Задача факторного анализа по отношению к только что рассмотренной является как бы противоположной. Она сводится к тому, чтобы по уже имеющейся матрице парных корреляций, аналогичной представленной в правой части показанного выше матричного равенства, отыскать одинаковые по включенным в них цифрам столбец и строку, умножение которых друг на друга по заданному правилу порождает корреляционную матрицу. Иллюстрация:
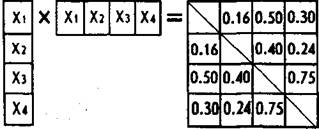
Здесь xvху х3 и хА — искомые числа. Для их точного и быстрого определения существуют специальные математические процедуры и программы для ЭВМ.
Допустим, что мы уже нашли эти цифры: хх = 0,45, х2= 0,36 х3 - 1,12, х4 = 0,67. Совокупность найденных цифр и называется фактором, а сами эти цифры — факторными весами или нагрузками.
Эти цифры соответствуют тем психологическим переменным, между которыми вычислялись парные корреляции. хх — характер, х2 — способности, х3 — потребности, х4 — успеваемость. Поскольку наблюдаемые в эксперименте корреляции между переменными можно рассматривать как следствие влияния на них общих причин — факторов, а факторы интерпретируются в психологических терминах, мы можем теперь от факторов перейти к содержательной психологической интерпретации обнаруженных статистических закономерностей. Фактор содержит в себе ту же самую информацию, что и вся корреляционная матрица, а факторные нагрузки соответствуют коэффициентам корреляции. В нашем примере х3 (потребности) имеет наибольшую факторную нагрузку (1,12), а х, (способности) — наименьшую (0,36).
584
Глава 3. Статистический анализ экспериментальных данных
Следовательно, наиболее значимой причиной, влияющей на все остальные психологические переменные, в нашем случае являются потребности, а наименее значимой — способности. Из корреляционной матрицы видно, что связи переменной х3 со всеми остальными являются наиболее сильными (от 0,40 до 0,75), а корреляции переменной х2 — самыми слабыми (от 0,16 до 0,40).
Чаще всего в итоге факторного анализа определяется не один, а несколько факторов, по-разному объясняющих матрицу интеркорреляций переменных. В таком случае факторы делят на генеральные, общие и единичные. Генеральными называются факторы, все факторные нагрузки которых значительно отличаются от нуля (нуль нагрузки свидетельствует о том, что данная переменная никак не связана с остальными и не оказывает на них никакого влияния в жизни). Общие — это факторы, у которых часть факторных нагрузок отлична от нуля. Единичные — это факторы, в которых существенно отличается от нуля только одна из нагрузок. На рис. 75 схематически представлена структура факторного отображения переменных в факторах различной степени общности.
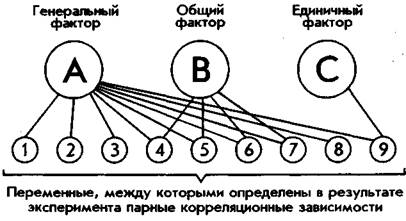
Рис. 75. Структура факторного отображения взаимосвязей переменных.
Отрезки, соединяющие факторы с переменными, указывают на высокие
факторные нагрузки
585
Часть II. Введение в научное психологическое исследование
СПОСОБЫ ТАБЛИЧНОГО И ГРАФИЧЕСКОГО ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
Результаты психолого-педагогического эксперимента, или психологического тестирования, кроме их текстового описания, можно представить в виде таблиц, схем, графиков, рисунков и т.п. Таблицы представляют собой упорядоченные по горизонтали и по вертикали наборы количественных и качественных данных, заключенных в рамки или без них. Таблицы могут иметь и не иметь названия, подзаголовки, указывающие на то, какие данные в них содержатся.
Таблицы строятся и оформляются не произвольно, а в соответствии с определенными правилами. Рассмотрим эти правила.
Таблицы, если их более двух-трех в тексте, нумеруются. Слово «таблица» обычно пишется справа или в середине вверху над таблицей. Непосредственно под ним располагается, если оно есть, название таблицы. Иногда для этого делаются примечания, касающиеся некоторых особенностей материала, содержащегося в таблице. Такие примечания помещаются, как правило, непосредственно под таблицей. Таблица имеет заголовки, которые указывают на то, что представлено в отдельных столбцах, а также рубрикацию по строкам, где обозначены особенности представляемого материала.
Рассмотрим в качестве примеров формы и способы построения типичных таблиц:
В таблице, построенной по образцу табл. 36, нет общего заголовка, который объединил бы названия всех столбцов, а есть только названия частных подзаголовков, относящиеся к отдельным столбцам. Нет также общего названия таблицы, так как содержание представленных в ней данных ясно само по себе. Имеются названия отдельных строк таблицы — без них было бы непонятно, что характеризуют собой цифры, имеющиеся в строках
586
Глава 3. Статистический анализ экспериментальных данных
Таблица 36
|
Начальные |
Средние классы, VI—VIII |
Старшие классы, IX-XI |
Количество учащихся |
120 |
130 |
100 |
Средний возраст (в годах) |
10,5 |
12,5 |
15 |
Успеваемость (средняя оценка) |
3,8 |
3,5 |
4,0 |
Уровень интеллектуального развития (IQ) |
102% |
104% |
105% |
таблицы. Подобного рода таблицы рекомендуется строить тогда, когда общее количество данных, представляемых в столбцах и строках таблицы, относительно невелико (не более четырех различных видов данных по столбцам и строкам, т.е. не более четырех столбцов и четырех строк). Во всех других случаях рекомендуется строить разграфленные таблицы с названиями, общими и частными подзаголовками (табл. 37).
Таблица 37 Результаты обследования шестилетних и семилетних детей с точки зрения их психологической готовности к обучению в школе (данные представлены в десятибалльной шкале оценок)
Возраст детей. Место их обучения и воспитания до поступления вшколу |
Основные показатели психологической готовности детей к обучению в школе |
|||||||||
интеллектуальные |
личностные |
межличностные |
||||||||
внимание |
воображение |
память |
мышление |
речь |
мотивы учения |
характер |
спо- |
об-щи-тель-ность |
контактность |
|
Шестилетние дети, посещавшие детский сад |
7,2 |
7,6 |
7,9 |
8,0 |
7,1 |
6,2 |
7,2 |
8,0 |
8,4 |
8,4 |
Шестилетние дети, воспитанные дома |
7,6 |
7,4 |
7,9 |
8,3 |
7,4 |
7,4 |
6,9 |
8,3 |
7,7 |
7,6 |
Семилетние дети, посещавшие детский сад |
7,9 |
8,0 |
8,1 |
8,4 |
8,3 |
8,2 |
7,3 |
8,6 |
8,9 |
9,0 |
Семилетние дети, воспитанные дома |
7,8 |
7,9 |
8,0 |
8,6 |
8,5 |
8,7 |
7,0 |
8,8 |
8,1 |
8,3 |
587
Часть II. Введение в научное психологическое исследование
В тех случаях, когда в таблице необходимо представить очень большое количество данных, которые невозможно полностью описать в подзаголовках столбцов или строк из-за громоздкости самих названий, обращаются к таблицам третьего типа (табл. 38), где соответствующие названия закодированы, а их расшифровка дается в примечании к таблице.
Таблица 38 Данные комплексного обследования детей из X классов средней школы
Условные обозначения детей |
Показатели обследования |
|||||||||||
I |
II |
III |
||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Примечание. А — Иванов, Б — Петров, В — Сидоров,...; I — социально-демографические данные о детях; II — успеваемость по отдельным предметам. III — данные о психологическом развитии; 1 — возраст, 2 — пол, 3 — социальное происхождение, 4 — место жительства, 5 — математика, 6 — физика, 7 — история, 8 — география, 9 — внимание, 10 — память, 11 — мышление, 12 — речь.
Другой способ представления экспериментальных данных — графический. График на плоскости представляет собой некоторую линию, которая изображает зависимость между двумя переменными, а график в пространстве — плоскость, представляющую зависимость между тремя переменными. При использовании двумерного графика по горизонтальной линии на плоскости обычно размещают независимую переменную — ту, которая изменяется по намерению экспериментатора и рассматривается в качестве возможной искомой причины. По вертикали располагают зависимую переменную — ту, которая является или рассматривается в качестве предполагаемой причины.
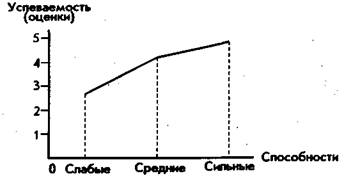
Рис. 76. График зависимости между способностями и успеваемостью учащихся1.
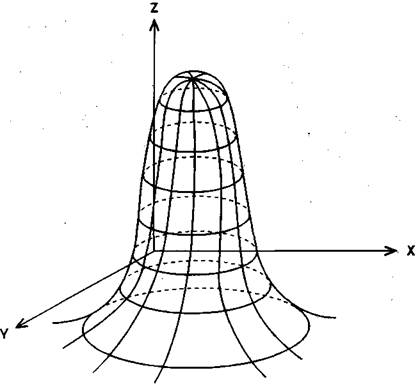
Рис. 77. Трехмерное распределение экспериментальных данных. По оси X —
уровень эмоционального возбуждения, по оси У— уровень тревожности,
по оси Z — продуктивность деятельности.
589
Часть II. Введение в научное психологическое исследование
Если речь идет о трехмерном, пространственном графике, то по линиям Xи Ybего горизонтальной плоскости чаще всего размещают независимые, а по линии Z в вертикальной плоскости — зависимую переменную. Однако могут быть отступления от этого правила. Они имеют место, например, тогда, когда в эксперименте изучаются одна независимая и две зависимые переменные. В этом случае данные, касающиеся независимых переменных, размещаются вдоль вертикальной оси X, а данные, относящиеся к зависимым переменным, — вдоль осей Yи Z.
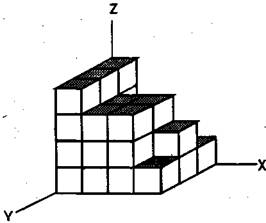 |
Рис. 79. Пример объёмной, или трёхмерной, гистограммы. |
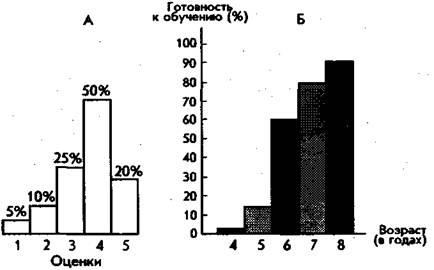
Рис. 78. Виды гистограмм «а плоскости. А — гистограмма распределения оценок в классе. Б — гистограмма распределения показателей готовности детей разного возраста к обучению в школе.
590
Глава 3. Статистический анализ экспериментальных данных
Рассмотрим два примера. На рис. 76 представлен плоскостной, а на рис. 77 — пространственный графики.
Графики могут строиться по отдельным точкам (рис. 76) или представлять собой непрерывные линии (плоскости, рис. 77).
Особую разновидность графических изображений экспериментальных результатов представляют собой гистограммы. Это столбчатые диаграммы (рис. 78), состоящие из вертикальных прямоугольников, расположенных основаниями на одной прямой. Их высота отражает степень или уровень развитости того или иного качества у испытуемого. Цифры, указывающие на частоту встречаемости качества в выборке испытуемых, размещаются или внутри столбцов гистограммы, или над ними, или по вертикальной оси графика. Иногда для наглядности, особенно в том случае, если гистограмма соответствует трехмерному пространству, ее изображают как объемную (рис. 79).
Контрольные вопросы
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Готтсданкер Р. Основы психологического эксперимента. М.:
МГУ, 1982. - 464 с.
(Корреляционные исследования: 378-424.)
2. ЗаксЛ. Статистическое оценивание. М., 1976.
(Что такое статистика: 37-39. Нормальная кривая и нормальное распределение: 63-71. Арифметическое среднее и стандартное отклонение: 72-79. Медиана и мода: 91-94. Распределение Стъюдента: 129-136. Хи-квадрат распределение: 136-150. Распределение Фишера: 150-153. Сравнение двух выборочных дисперсий из нормальных совокупностей: 241-245. Сравнение двух выборочных средних из нормальных совокупностей: 245-270. Проверка распределений по хи-квадрат критерию согласия: 295-296. Коэффициент ранговой корреляции Спирмена: 368-372. Оценивание прямой регрессии: 371-381. Проверка равенства нескольких дисперсий: 448-453).
3. Кулагин Б.В. Основы профессиональной психодиагностики. Л.,
1984.-216 с.
(Измерение в психодиагностике: 13-20. Корреляция и факторный анализ: 20-33.)
4. Фресс П., Пиаже Ж. Экспериментальная психология. Вып. I и П.
М., 1966.
(Измерение в психологии: 197-229. Проблема надежности измерения: 229-231).
5. Практикум по общей психологии / Под ред. А.И. Щербакова.
М., 1990.-287 с.
[Методы психологии (с элементами математической статистики): 20-39].
6. Психодиагностические методы (в комплексном лонгитюдном
исследовании студентов) / Под ред. А.А. Бодалева, М.Д. Дворя-
шиной, И.М. Палея. Л., 1976. - 248 с.
(Основные математические процедуры психодиагностического исследования: 35-51.)
Ваш комментарий о книге
Обратно в раздел психология
