Боди З., Мертон Р. Финансы

ОГЛАВЛЕНИЕ

Глава 12 ФОРМИРОВАНИЕ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ

В этой главе...
• Сущность теоретических и практических аспектов формирования инвестиционного портфеля
• Модель формирования инвестиционного портфеля, которая устанавливает баланс между риском и доходностью

Содержание
12 1 Процесс формирования инвестиционного портфеля
12 2 Доходность и риск. в поисках баланса
M123 Эффективная диверсификация портфеля при наличии многих рискованных активов

Эта глава посвящена тому, как людям следует инвестировать свои средства, т е. проблеме формирования инвестиционного портфеля (potrfohoselection) В инвестиционный портфель включены все личные активы (акции, облигации, паи в бизнесе, дом или квартира, пенсия, страховые полисы и т.д) и все личные обязательства (ссуда на обучение, ссуда на приобретение автомобиля, закладная под недвижимость и пр ).
Не существует единой стратегии формирования инвестиционного портфеля, которая подходила бы абсолютно всем. Зато имеется несколько общих принципов, в частности принцип диверсификации, которые годятся для всех людей, склонных к неприятию риска (risk-averse) В главе 11 мы обсуждали диверсификацию как один из методов управления риском В этой главе мы продолжим это обсуждение, а также рассмотрим метод количественного анализа оптимального соотношения между риском и ожидаемым уровнем доходности портфеля.
В разделе 12 1 мы опишем формирование портфеля с точки зрения процесса финансового планирования на различных этапах жизни человека (его жизненного цикла) и покажем, почему нет стратегии, которая одинаково хорошо подходила бы всем без исключения. Тут же мы узнаем, почему на формирование портфеля оказывают влияние такие факторы, как горизонт прогнозирования (time horizon) и терпимость к риску (nsk tolerance). В разделе 12.2 будет проанализирован выбор между единичными рискованными и безрисковыми активами, а в разделе 12.3 мы поговорим об оптимальном варианте формирования портфеля, включающего несколько рискованных активов.

12.1. ПРОЦЕСС ФОРМИРОВАНИЯ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ

Формирование инвестиционного портфеля заключается в распределении инвестиций конкретным человеком. Это процесс поиска наилучшего соотношения между риском и ожидаемым уровнем доходности инвестиций с целью составления портфеля, в котором активы и обязательства сочетались бы с этой точки зрения оптимальным образом. В более узком смысле формирование портфеля трактуется только как принятие решений относительно сумм, которые следует инвестировать в акции, облигации и другие ценные бумаги. Если рассматривать формирование портфеля шире, то в него можно включить вопросы о том, что предпочтительнее — покупка жилья или его аренда; какого типа страховку покупать и сколько для этого выделить средств, а также решение о том, каким образом следует управлять своими обязательствами. Еще более расширенное толкование формирования портфеля включает рассмотрение таких вопросов как определение суммы, которую целесообразно инвестировать в накопление челове ческого капитала (например, в продолжение профессионального обучения). Общим элементом всех этих решений является поиск наилучшего соотношения между риском и ожидаемым уровнем доходности.
Эта глава посвящена исследованию концепций и методов, которые требуются для определения соотношения риск/доходность и для управления эффективностью портфеля. Основная идея заключается в том, что даже при наличии ряда общих правил формирования портфеля, которые подходят буквально всем людям, не существует единой модели портфеля или единой стратегии его формирования выбора, которыми могли бы пользоваться абсолютно все. Сейчас мы объясним, почему это так.

12.1.1. Жизненный цикл семьи

Стратегия формирования портфеля зависит от конкретных обстоятельств каждого человека (возраста, семейного положения, рода занятий, дохода, общего благосостояния и т.д.). Поэтому один человек, вкладывая деньги в некие ценные бумаги, увеличивает свой риск, а для другого покупка тех же ценных бумаг приводит к снижению риска. К тому же ценные бумаги, которые снижают рискованность вложений на начальных стадиях жизненного цикла семьи, могут дать совершенно противоположный эффект на поздних.
Для молодой четы, начинающей семейную жизнь, оптимальным вложением является приобретение дома и получение ссуды под залог этого дома. Для супругов пред-пенсионного возраста оптимальным решением может стать продажа дома и вложение полученных средств в ценные бумаги, что обеспечит устойчивые и регулярные денежные поступления до конца их жизни.
Рассмотрим вопрос страхования жизни. Допустим, что перед нами два человека1:
Мириам, на руках у которой несовершеннолетние дети, и Санджив, одинокий мужичина без детей и других иждивенцев. Несмотря на то что во многих отношениях — возраст, доход, род занятий, уровень благосостояния и т.п., — они не отличаются друг от друга, у каждого из них существует свой оптимальный вариант страхования. Цель Мириам — обезопасить семью в случае своей смерти, поэтому ей нужен полис, который предусматривает денежные выплаты детям в случае смерти владельца полиса. Санджива не интересуют выплаты после его смерти, следовательно, для него страхование жизни не является действием, снижающим риск. На более поздней стадии жизни, когда Мириам убедится, что ее дети в состоянии сами позаботиться о себе, ей не нужна будет защита, которую дает полис страхования жизни, у
Теперь представим, что Мириам и Санджив достигли пенсионного возраста. Мириам есть дети, и она не волнуется о том, что будет с ее сбережениями поел смерти, Они будут унаследованы ее детьми. Если же она проживет очень долго и растратит свои сбережения, то, безусловно, ее дети смогут оказать ей финансовую поддержку.
Санджив же одинокий человек, и у него нет никого, кому он мог бы оставить наследство. Он намерен израсходовать все свои сбережения, пока жив, однако его беспокоит то обстоятельство, что если он проживет слишком долго и при этом будет слишком активно тратить деньги, то их не хватит до конца жизни. Санджив сможет снизить риск нехватки сбережений путем покупки страхового полиса, гарантирующего ему пожизненный доход. Такой страховой полис, обеспечивающий пожизненные выплаты, называется пожизненной рентой (life annuity). Для Мириам же подобный вид страхования не снизит риска ее инвестиций.
Как ясно из приведенных примеров, даже у людей одинакового возраста, с одинаковым уровнем дохода и благосостояния, перспективы, связанные с покупкой дома или приобретением страхового полиса, различны. То же самое можно сказать и о покупке акций, облигаций и других ценных бумаг. Ни один из инвестиционных портфелей нельзя считать равно подходящим всем инвесторам.
Чтобы убедиться в этом, рассмотрим двух инвесторов одного возраста и одинакового семейного положения. Чангу 30 лет; он работает финансовым аналитиком на Уолл-Стрит. Его нынешний и будущий заработок в значительной степени зависит от состояния рынка ценных бумаг. Оби тоже 30 лет; она преподает английский язык в государственной школе. Ее нынешнее и будущее жалованье не слишком зависит от конъюнктуры рынка ценных бумаг. Следовательно, для Чанга помещение большей части его инвестиционного портфеля в акции является мероприятием более рискованным, чем для Оби.

12.1.2. Горизонты прогнозирования

Составление плана формирования наилучшего портфеля начинается с определения целей инвестора и горизонтов прогнозирования. Период, или горизонт планирования {planninghorizon) — это весь промежуток времени, на который составляются планы инвестора.
Самый протяженный горизонт прогнозирования обычно охватывает период до выхода на пенсию и обычно сопоставим с индивидуальной продолжительностью жизни1. Значит, у молодого человека 25 лет, рассчитывающего прожить до 85 лет, горизонт планирования равен 60 годам. По мере старения горизонт планирования становится все короче и короче (см. врезку 12.1).
Период, или горизонт пересмотра решения (decisionhorizon) — это промежуток времени между двумя решениями, касающимися формирования инвестиционного портфеля. Продолжительность периода пересмотра решений устанавливается каждым человеком индивидуально.
Некоторые инвесторы производят пересмотр своих портфелей через определенные интервалы, например раз в месяц (при оплате счетов) или раз в год (при заполнении налоговой декларации). Инвесторы со средним достатком, у которых основная часть ережений находится на банковских счетах, пересматривают свои инвестиционные портфели довольно редко и нерегулярно, обычно в связи с такими не часто случающимися событиями, как женитьба или развод, появление ребенка или получение наследства Причиной для пересмотра инвестиционного портфеля могут стать также резкие колебания цен на те или иные активы, которыми владеет данный индивидуум
Инвесторы, вложившие значительные суммы в акции и облигации, могут пересматривать свой портфель ежедневно, а иногда и чаще. У них самым коротким периодом пересмотра решения является период биржевых торгов (tradinghonwn); именно он определяет минимальный промежуток времени, через который инвестор пересматривает свой портфель.
Индивидуум не может контролировать протяженность периода биржевых торгов. Период биржевых торгов может равняться неделе, дню, часу или даже минуте — в зависимости от структуры рынка в данной экономической системе (например, от того, в какое время открыты биржи ценных бумаг, и от того, существуют ли организованные внебиржевые рынки).
В условиях сегодняшней глобализации финансовой среды покупка и продажа большинства ценных бумаг может быть осуществлена в любой точке земного шара в любое время дня и ночи. Следовательно, для таких ценных бумаг горизонт биржевых торгов очень короток.

Врезка 12.1
Расчет ожидаемой продолжительности жизни
Ожидаемая продолжительность жизни — это количество лет, которое вы рассчитываете прожить. Данный показатель рассчитывается на основании статистических данных о смертности, которые собираются и анализируются актуариями. Актуарий — это специалист, который с помощью математических методов рассчитывает страховые премии.
Чтобы оценить вероятность смерти в том или ином возрасте, актуарий использует статистические таблицы смертности (одна из них — для жителей США — представлена ниже в этом разделе). В таблице указан коэффициент смертности на 1000 человек и ожидаемая продолжительность жизни (ожидаемое значение числа лет, оставшихся до смерти) для нескольких категорий возрастов от 65 до 95 лет. Статистические данные по смертности среди мужчин и женщин представлены отдельно.

Источник. Commissioners Standard Ordinary (CSO) Mortality Table.

Второй столбец таблицы показывает, что среди 60-летних мужчин вероятность смерти в период до достижения ими 61 года составляет 0,1608 (16,08/1000), вероятность смерти в период до достижения 62 лет составляет 0,1754 и т.д. В третьем столбце показана ожидаемая продолжительность жизни для мужчин каждого возраста, рассчитанная с помощью коэффициентов смертности, показанных во втором столбце. Таким образом, ожидаемая продолжительность жизни 60-летнего мужчины равна 17,51 лет, мужчины в возрасте 61 года — 16,79 лет и т.д. Вероятность умереть до достижения 96 лет у 95-летнего мужчины равна 0,32996; его ожидаемая продолжительность жизни — 1,87 года. В столбцах 4 и 5 показаны соответствующие статистические данные для женщин.

Сегодняшние решения о составе инвестиционного портфеля основываются на предположениях о том, что может произойти завтра. План, при разработке которого сегодняшние решения принимаются с учетом ваших последующих действий, называется стратегией.
При формулировании стратегии инвестирования крайне важным фактором является частота, с которой инвестор пересматривает свой портфель, покупая или продавая ценные бумаги. Например, инвестор выбирает стратегию инвестирования "избыточного" капитала в акции. "Избыточным" в данном случае является капитал, превышающий некий предел, необходимый ему для поддержания определенного уровня жизни. Если курс этих акций со временем пойдет вверх, то инвестор увеличит долю портфеля, отведенную на вложения в эти акции. Однако, если акции станут дешеветь, инвестор уменьшит долю вложенных в них капиталов. Если курс акций снизится до такого предела, что привычный стандарт жизни окажется под угрозой, инвестор вообще избавится от этих акций.

12.1.3. Толерантность к риску

Индивидуальная толерантность (tolerance) к риску — важнейший фактор при формировании инвестиционного портфеля2. Можно считать, что толерантность к риску находится под влиянием таких факторов, как возраст, семейное положение, род деятельности, уровень благосостояния и т.п., т.е. факторов, которые влияют на возможности человека поддерживать привычный ему уровень жизни в случае неблагоприятных изменений в состоянии инвестиционного портфеля. Отношение инвестора к риску также играет роль в определении его индивидуальной толерантности к риску. Даже если Рассматривать людей примерно одного возраста, семейного положения и рода деятельности, то можно заметить, что одни более склонны рисковать, чем другие.
Когда при анализе проблемы выбора активов для формирования оптимального портфеля мы говорим о толерантности инвестора к риску, то не проводим различий между способностью рисковать и отношением к риску. Следовательно, не имеет значения, по какой причине инвестор отличается высокой толерантностью к риску — потому ли, что он молод и богат, потому ли, что он легко переносит неудачи, или же по причине уверенности в том, что нельзя упускать шанс. Для нашего анализа имеет значение только то, что для достижения более высокого ожидаемого уровня доходности вложений он быстрее, чем средний инвестор, согласится на более высокий риск.
В главе 10 мы также использовали термин неприятие риска. Чем более толерантен человек к Риску, тем меньше он его избегает

12.1.4. О роли профессионального управляющего активами

У большинства людей нет ни специальных знаний, ни времени на оптимизацию инвестиционных портфелей. Для выполнения этой операции они либо нанимают консультанта по инвестициям, либо вообще покупают "конечный продукт" в виде готового портфеля активов, который им предлагают финансовые посредники. Среди "конечных продуктов" присутствуют разнообразные счета для инвестиционных операций, а также взаимные фонды, которые предлагаются компаниями, ведущими операции с ценными бумагами, банками, инвестиционными и страховыми компаниями.
Когда финансовые посредники решают, какой набор активов предложить конкретному домохозяйству, они находятся примерно в том же положении, что и повар ресторана составляющий меню. У них множество "ингредиентов" — наиболее популярных на рынке акций, облигаций и других ценных бумаг, выпускаемых различными компаниями и правительством, — и бесконечное число их комбинаций. Однако клиентам надо предложить ограниченное число элементов. Портфельная теория, о которой мы более подробно поговорим ниже в этой главе, устанавливает определенные ориентиры, помогающие выбрать такое количество составляющих портфеля, которое, с одной стороны, не слишком велико, а с другой — максимально соответствует всему спектру запросов клиентов.

12.2. ДОХОДНОСТЬ И РИСК: В ПОИСКАХ БАЛАНСА

В двух следующих разделах рассмотрены последовательные этапы анализа, который применяется профессиональными управляющими инвестиционных портфелей для исследования количественного соотношения между риском и ожидаемым уровнем доходности. Его поиск выполняется с единственной целью — сформировать портфель, инвестиции в который обеспечивали бы инвестору максимальную ожидаемую ставку доходности при той степени риска, на которую он согласен. В процессе анализа мы будем говорить о рискованных активах (riskyassets), не подразделяя их на облигации, акции, опционы, страховые полисы и пр., потому что, как уже говорилось выше в этой главе, степень рискованности каждого отдельного актива зависит в первую очередь от конкретных обстоятельств жизни данного инвестора.
Оптимизация портфеля обычно состоит из двух этапов: (1) выбора оптимальной комбинации рискованных активов и (2) объединения полученного оптимального набора рискованных активов с безрисковыми активами. В целях упрощения процесса мы начнем со второго этапа — объединения портфеля, содержащего рискованные активы, с безрисковыми активами. (Какие именно активы следует считать безрисковыми, мы уточним в следующем разделе.) Этот единственный рискованный портфель составлен из множества рискованных активов, скомбинированных оптимальным образом. В разделе 12.3.4 будет показано, как определяется оптимальный состав портфеля с рискованными активами.

12.2.1. Что такое безрисковые активы

В главе 4 мы рассматривали процентные ставки, и там же было показано, что существуют безрисковые финансовые активы для каждой расчетной денежной единицы (доллара, иены и т.д.) и для каждого из возможных сроков погашения. Например, если перед нами облигация со следующими характеристиками — десятилетний период обращения, деноминированная в долларах, бескупонная, свободная от риска дефолта, доходность при пога шении составляет 6% годовых, — то она может быть безрисковым активом только в долларовой зоне и только в том случае, если будет находиться у владельца до срока погашения. Если облигация будет продана до срока погашения, то точно о ее долларовой доходности сказать нельзя, потому что неясно, какой будет цена продажи. И даже если владелец не продаст ее до срока погашения, ставка доходности облигации, деноминированной в иенах или в единицах покупательской способности, может быть неопределенной по причине колебания в будущем обменного курса или потребительских цен.
В теории формирования наилучшего портфеля безрисковым активом считается ценная бумага, которая предлагает полностью предсказуемую ставку доходности в расчетных денежных единицах, выбранных для анализа, и в пределах периода пересмотра решения данного инвестора. Если брать более общую ситуацию, когда нет конкретного инвестора, то безрисковыми активами следует считать те из них, которые предлагают инвестору предсказуемую ставку доходности в пределах периода биржевых торгов (т.е. самого короткого периода принятия решений).
Следовательно, если за расчетную денежную единицу принят доллар США, а период биржевых торгов составляет один день, то безрисковой ставкой доходности является процентная ставка казначейских векселей со сроком погашения на следующий день.

12.2.2. Объединение безрискового актива с единственным рискованным активом

Предположим, что вы решили инвестировать 100000 долл. Перед вами безрисковый актив с процентной ставкой 0,06 годовых и рискованный актив с ожидаемой ставкой доходности в 0,14 годовых и стандартным отклонением в 0,203. Какую часть от 100000 долл. вам следует вложить в рискованный актив4?
Все доступные комбинации риска и доходности показаны в табл. 12.1 и на рис. 12.1. Начнем с ситуации, когда вы вкладываете все свои деньги в безрисковый актив (точка F на. рис. 12.1 и первая строка в табл. 12.1). Столбец 2 в табл. 12.1 показывает долю портфеля, инвестированную в рискованный актив (0), а столбец 3 — долю портфеля, инвестированную в безрисковый актив (100%). При сложении доли всегда дают 100%. Столбцы 4 и 5 табл. 12.1 содержат ожидаемую доходность и стандартное отклонение, соответствующие портфелю F: Е(г), равную 0,06 в год, и о, равную 0,00.
Ситуация, когда вы инвестируете все свои деньги в рискованный актив, соответствует точке S на рис. 12.1 и последней строке в табл. 12.1. В этом случае ожидаемая или средняя доходность равна 0,14, а ее стандартное отклонение составляет 0,20.
На рис. 12.1 ожидаемая ставка доходности портфеля, Е(г), показана на вертикальной оси, а стандартное отклонение, <т, — на горизонтальной. Доли портфеля неявно отражены в данных рис. 12.1 и более точно представлены в табл. 12.1.
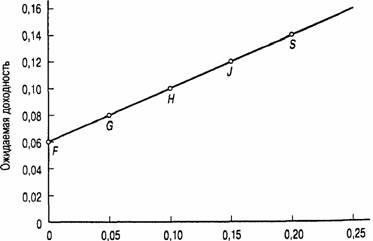
На рис. 12.1 в графическом виде показаны соотношения между риском и доходностью. Линия на рис. 12.1, соединяющая точки F, G, H, J и S, представляет набор (портфель) свободно доступных вам вариантов из рискованного и безрискового акти-в5. Каждая точка на линии соответствует портфелю из этих двух видов активов, представленных в столбцах 2 и 3 в табл. 12.1.
Определение и формулы для вычисления ожидаемой (средней) ставки доходности и ее стандартного отклонения можно найти в разделах 10.8 и 10.9. Обратите внимание, что в данной главе мы Указываем ставки доходности как десятичные числа, а не как процентные значения.
В данном разделе активы и ценные бумаги — синонимы. — Прим. ред
В качестве безрискового актива могут выступать, например, казначейские векселя США, а Ркованного — акции какой либо корпорации. — Прим. ред.

В точке F, которая на рис. 12.1 расположена на вертикальной оси, при Е(г), равной 0,06 в год, и сг, равной 0, все ваши деньги вложены в безрисковый актив. Вы ничем не рискуете, и ваша ожидаемая доходность составляет 0,06 в год. Чем больше денег вы изымаете из безрискового актива, помещая их в рискованный, тем дальше вы двигаетесь вправо по линии, обозначающей соотношение риск/доходность. При этом степень риска повышается, но и ожидаемая доходность увеличивается. Если же все ваши деньги вложены в рискованный актив, вы окажетесь в точке S с ожидаемой доходностью Е(г) в 0,14 и стандартным отклонением о-в 0,20.

Таблица 12.1. Ожидаемая доходность и стандартное отклонение портфеля в связи с долей средств, инвестированной в рискованны) актив

Стандартное отклонение
Рис. 12,1. Соотношение между риском и ожидаемой доходностью инвестиционного портфеля

Примечание. Точке F соответствует ситуация, когда портфель на 100% состоит из инвестиций в безрисковые ценные бумаги с доходностью 0,06 годовых. Точке S соответствует ситуация, когд 100% инвестиций сделано в рискованные активы с ожидаемой доходностью 0,14 годовых и < равным 0,20. В точке // портфель наполовину состоит из рискованных, наполовину — из рисковых активов.
Портфель //(соответствующий третьей строке в табл. 12.1) наполовину состоит, наполовину— из безрискового. Если 50% суммы вложено рискованные ценные бумаги, а 50% — в безрисковые, ожидаемая доходность будет находиться посередине между ожидаемой ставкой доходности портфеля, полностью состоящего из акций, т.е. рискованных активов (0,14), и процентной ставкой, которую гарантируют безрисковые активы (0,06). Ожидаемая ставка доходности (0,10) показана в столбце 4, а стандартное отклонение (0,10) — в столбце 5.

Теперь давайте разберемся, как на рис. 12.1 можно определить состав портфеля для любой точки, лежащей на прямой риск/доходность, а не только для точек, представленных в табл. 12.1. Предположим, например, что мы хотим определить состав портфеля, для которого ожидаемая ставка доходности равна 0,09. Судя по рис. 12.1, точка, соответствующая такому портфелю, лежит на прямой риск/доходность между точками G и Н. Но каков точно состав портфеля и его стандартное отклонение? Чтобы ответить на этот вопрос, нам понадобится формула, описывающая график соотношения риска и доходности, которая связала бы все точки на рис. 12.1. Поступите следующим образом, разбив ваши действия на ряд последовательных этапов.
Этап 1. Определите соотношение между ожидаемой доходностью и долей инвестиций, приходящейся на рискованный актив.
Пусть w обозначает долю от 100000 долл., которая вложена в рискованный актив. Оставшаяся часть будет равна (I - w); и она вложена в безрисковый актив. Ожидаемая ставка доходности портфеля Е(r) задана формулой:
(12.1)
где Е (r) обозначает ожидаемую ставку доходности рискованного актива, а rf — безрисковая ставка доходности. Подставив вместо значение 0,06, а вместо Е (r) — 0,14, получим:
E (r)= 0,06 + w (0,14-0,06) = 0,06 + 0,08w
Уравнение 12.1 интерпретируется следующим образом. Базовой ставкой доходности для любого портфеля является безрисковая ставка доходности (0,06 в нашем примере). Кроме того, предполагается, что инвестиции в портфель принесут дополнительную премию за риск, которая зависит от (1) премии за риск по рискованному активу E (rs) - rf (0,08 в нашем примере) и от (2) доли портфеля, инвестированной в рискованный актив и обозначенной w.
Чтобы определить состав портфеля, соответствующий ожидаемой ставке доходности в 0,09, надо подставить нужные значения в уравнение 12.1 и вычислить w.
0,09=0,06+0,08w
(0.09-0,06), 0,08
Таким образом, портфель на 37,5% состоит из рискованного актива, а на 62,5% — из безрискового.
Этап 2. Определите связь между стандартным отклонением и долей инвестиций, приходящихся на рискованный актив.
Если в одном портфеле объединены рискованный и безрисковый активы, то стандартное отклонение доходности такого портфеля равно стандартному отклонению доходности рискованного актива, умноженному на его вес в портфеле. Обозначив стандартное отклонение рискованного актива как оsполучим формулу стандартного отклонения доходности портфеля:
Чтобы определить стандартное отклонение, соответствующее ожидаемой ставке доходности в 0,09, подставим в уравнение 12.2 вместо w значение 0,375 и вычислим s
s =ssw =0,2х0,375 =0,075
Таким образом, стандартное отклонение доходности портфеля составило 0 075. Наконец, мы можем убрать w, чтобы вывести формулу, напрямую связывающую ожидаемую ставку доходности со стандартным отклонением на прямой риск/доходность.
Этап 3. Определите соотношение между ожидаемой ставкой доходности и стандартным отклонением.
Чтобы вывести точное уравнение, описывающее прямую риск/доходность на рис 12.1, надо видоизменить уравнение 12.2 и представить w как соотношение о/о. Подставив это соотношение вместо w в уравнение 12.1, получим:

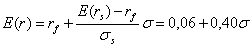
Другими словами, ожидаемая ставка доходности портфеля, выраженная как функция его стандартного отклонения, представляет собой прямую линию, пересекающую вертикальную ось в точке t[ == 0,06 и наклоном, равным:

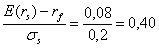
Угол наклона прямой характеризует дополнительную ожидаемую доходность, предлагаемую рынком для каждой дополнительной единицы риска, которую согласен нести инвестор.

12.2.3. Как получить заданную ожидаемую доходность: пример 1
Давайте определим состав портфеля, ожидаемая ставка доходности которого соответствовала бы значению 0,11 в год. Каким будет в этом случае стандартное отклонение доходности?
Решение
Чтобы определить состав портфеля с ожидаемой ставкой доходности в 0,11, нэл0 подставить данные в уравнение 12.1 и найти w.
0,11 =0,06+0,08w

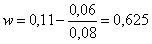
Следовательно, в портфеле содержится 62,5% рискованного актива и 37,5% безрискового.
Чтобы определить стандартное отклонение, соответствующее ожидаемой ставке доходности в 0,11, надо в уравнении 12.2 вместо w подставить значение 0,625 и определить s.
s= 0,2w= 0,2х0,625 =0,125
Следовательно, стандартное отклонение доходности портфеля равно 0,125

12.2.4. Концепция эффективности портфеля

Эффективным портфелем (efficient portfolio) мы называем такой портфель, который предлагает инвестору максимально возможный ожидаемый уровень доходности при заданном уровне риска.
Чтобы объяснить значение концепции эффективности портфеля и показать, как получить действительно эффективный портфель, давайте рассмотрим предыдущий пример, дополнительно включив в него еще один рискованный актив. Рискованный актив 2 имеет ожидаемую ставку доходности 0,08 в год и стандартное отклонение 0.15. Он представлен точкой R на рис. 12.2.
Инвестор, который хоче1 получить ожидаемую ставку доходности в 0.08 годовых, может добиться своей цели, вложив всю сумму в рискованный актив 2. Тогда он окажется в ситуации, описываемой точкой R. Но при этом портфель инвестора неэффективен, потому что в точке G инвестор может получить такую же ожидаемую ставку доходности (0,08 в год) при меньшем значении стандартного отклонения.
Из табл. 12.1 видно, что в точке G стандартное отклонение составляет только 0,05. Это объясняется тем, ч-ю 25% инвестиций данного портфеля вложены в рискованный актив 1, а 75% — в безрисковый актив. Действительно, не желающий рисковать инвестор выберет на прямой риск/доходность, соединяющей точки G и S, любую точку — только не точку R. Любая из этих точек соответствует вполне приемлемой ситуации, когда некоторое количество рискованного актива 1 уравновешивается безрисковым активом. Например, портфель в точке J имеет стандартное отклонение, равное стандартному отклонению рискованного актива 2 (о = 0,15), но его ожидаемая ставка доходности составляет 0,12 годовых, а не 0,08. Из табл. 12.1 нам известно, что такое соотношение соответствует портфелю, который на 75% состоит из рискованного актива 1 и на 25% из безрискового актива.
С помощью уравнений 12.1 и 12.2 можно определить состав других эффективных портфелей, которые описываются точками между G и J и имеют, следовательно, более высокую ожидаемую ставку доходности и меньшее значение стандартного oтклонения в сравнении с рискованным активом 2. Рассмотрим, например, портфель, который на 62,5% состоит из рискованного актива 1 и на 37,5 % — безрискового актива. Его ожидаемая ставка доходности равна 0,11 в год, а стандартное отклонение составляет 0,125.

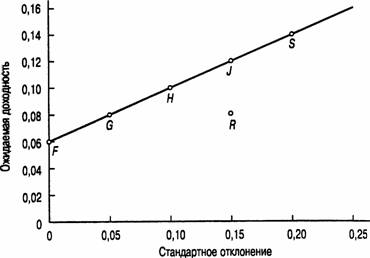
Рис. 12.2. Эффективность портфеля
Примечание. В точке R портфель на 100% состоит из инвестиций, вложенных в рискованный актив 2 с ожидаемой ставкой доходности 0,08 и s = 0,15. Инвестор может получить более высокую ожидаемую доходность и меньшее стандартное отклонение в любой точке прямой, проходящей через точки G и J.

12.3. ЭФФЕКТИВНАЯ ДИВЕРСИФИКАЦИЯ ПОРТФЕЛЯ 1РИ НАЛИЧИИ МНОГИХ РИСКОВАННЫХ АКТИВОВ

Рабочая книга Несмотря на то что инвестирование исключительно в рискованный актив 2 само по себе неэффективно, может быть, имеет смысл объединить в одном портфеле два вида рискованных активов? Или добавить к двум видам рискованных активов безрисковые?
Мы исследуем способы эффективного объединения трех активов в два этапа. На 1ервом этапе мы рассмотрим соотношение риска и доходности, достигаемое объединением только рискованных активов 1 и 2; на втором этапе мы добавим к ним безрисковый актив.

12.3.1. Портфели из двух рискованных активов

Объединение в одном портфеле двух видов рискованных активов аналогично объединению рискованного актива с безрисковым; эта тема обсуждалась в разделе 12.2. Просмотрите еще раз табл. 12.1, рис. 12.1 и уравнения 12.1 и 12.2.) Если один из двух активов безрисковый, то стандартное отклонение его ожидаемой ставки доходности и корреляция с другим активом равны нулю. Если оба актива являются рискованны-, w, то так или иначе необходим анализ соотношения риск/доходность.
Формула для вычисления среднего значения ставки доходности любого портфеля, в котором w — это доля рискованного актива 1, а (1 - w) — это доля рискованного актива 2, имеет следующий вид:
Е(r) = wE(r1)+(l-w)E(r2)                 (12.4)
В свою очередь формула дисперсии такова:
s2 = s12 + (1 - w)2 s2 + 2w (1 - w) ps1 s2 (12.5)
Эти два уравнения можно сравнить с уравнениями соответственно 12.1 и 12.2. Сравнение 12.4 — это, по сути, уравнение 12.1, только вместо процентной ставки безрискового актива rr в него вставлена ожидаемая доходность рискованного актива 2, Е (r2) Уравнение 12.5 — это более общая форма уравнения 12.2. Если актив 2 безрисковой, то s2 = 0 и уравнение 12.5 упрощается до вида уравнения 12.2. В табл. 12.2 сведены наши оценки распределения вероятности ставок доходности скованных активов 1 и 2. Обратите внимание: мы исходим из предположения, что коэффициент корреляции равен нулю (р = 0).
В табл. 12.3 и в рис. 12.3 показаны комбинации средних значений и стандартных отклонений доходностей, которые можно получить при объединении в одном портфеле рискованного актива 1 и рискованного актива 2. Точка S на рис. 12.3 соответствует портфелю, который состоит исключительно из рискованного актива 1, а точка R — портфелю, состоящему исключительно из рискованного актива 2.
Давайте покажем, как ожидаемые ставки доходности и стандартные отклонения в In 12.3 рассчитываются по формулам 12.4 и 12.5. Рассмотрим портфель С, который эит на 25% из рискованного актива 1 и на 75% — из рискованного актива 2.

Соотношение риск/доходность для портфелей с двумя рискованными
eSllleSltESgeKe&eiBe

1одставив необходимые значения в уравнение 12.4, мы найдем, что ожидаемая ва доходности в точке С составит 0,095 в год:
jE'(r)=0,25 E(r,) +0,75 E{r} =0,25х0,14 +0,75х0,08 =0,095 ставив в уравнение 12.5 значение w, мы выясним, что стандартное отклонение

(Т2 = W22 + (1 - w) (72 + 2w (1 - w) pO'iO'2
=0,252x0,22+0,752x0,152+0 =0,01515625
о- =УО,01515625 =0,1231

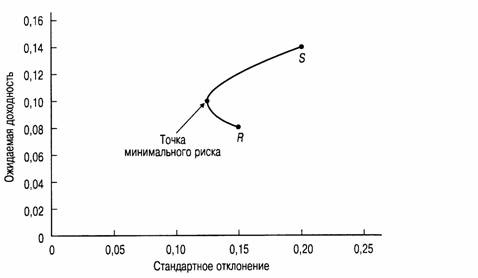
Рис. 12.3. Кривая соотношения риск/доходность: только рискованные активы
Примечание. Предполагается, что ?'("/•=0,14, о-/=0,20, E(r)=0,OS, crj=0,15, /т=0.
Давайте с помощью табл. 12.3 исследуем кривую, соединяющую на рис. 12.3 точки R и S. Начнем с точки R и переместим часть наших капиталов из рискованного актива 2 в рискованный актив 1. При этом наблюдается не только повышение средней ставки доходности, но и снижение стандартного отклонения. Оно снижается до тех пор, пока мы не получим портфель, который на 36% состоит из инвестиций в рискованный актив 1 и на 64% — в рискованный актив 26.
Эта точка характеризует портфель с минимальной дисперсией (minimum-variance portfolio), состоящий из рискованного актива 1 и рискованного актива 2. Если в рискованный актив 1 инвестируется более 36% общего капитала, то стандартное отклонение портфеля увеличивается.

6 Формула, описывающая долю рискованного актива 1, которая минимизирует дисперсию портфеля, выглядит следующим образом:

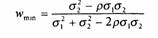
12.3.2. Оптимальная комбинация рискованных активов

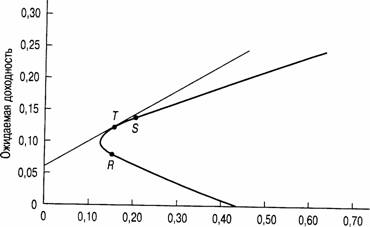
Теперь давайте рассмотрим комбинации риск/доходность, которые мы можем подучить посредством объединения безрискового актива с рискованными активами 1 и 2. На рис. 12.4 показано графическое представление всех возможных комбинаций риск/доходность; этот рисунок показывает также, как можно получить оптимальную комбинацию рискованных активов для объединения с безрисковым активом.

Стандартное отклонение
Рис. 12.4. Оптимальная комбинация рискованных активов Примечание. Предполагается, что Гу=0,06, ?/-=0,14, сг/=0,20, ?)=0,08, сг;=0,15, /?=0.

Сначала проанализируем прямую линию, соединяющую точку F с точкой S. Она нам уже знакома, поскольку представляет собой график соотношения риск/доходность, который мы видели на рис. 12.1. Прямая показывает ряд комбинаций риск/ доходность, которые могут быть получены посредством объединения безрискового актива с рискованным активом 1.
Прямая линия, соединяющая точку Fc любой точкой кривой, соединяющей точки R и S, представляет собой график, описывающий соотношение риск/доходность для всех комбинаций следующих трех активов: рискованных активов 1 и 2 с безрисковыми активами. Наибольшие значение этого соотношения, которого мы можем достичь, находится на линии, соединяющей точки F и Т. Точка Т является общей точкой прямой линии, выходящей из точки F, и кривой, соединяющей точки R и S. Мы называем такой рискованный портфель, который соответствует общей точке Г на рис. 12.4, оптимальной комбинацией рискованных активов. Именно объединением этого портфеля рискованных активов с безрисковым активом достигается формирование максимально эффективного портфеля. Формула для определения долей портфеля в точке Г такова:

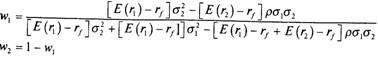
Подставляя данные в это уравнение, получаем, что оптимальной комбинацией Рискованных активов (для портфеля в точке пересечения с прямой, который еще называют тангенциальным портфелем (thetangencyportfolio)), является 69,23% рискованного актива 1 и 30,77% рискованного актива 2. Это означает, что ставка доходности Е(г-г), и стандартное отклонение, оу, равны:
?(/y)=0,122 От =0,146
Следовательно, новый график для эффективного соотношения риск/доходность задан формулой:
где угол наклона — отношение доходности к риску — равен 0,42. Сравним полученное выражение с формулой для прежней линии соотношения риск/доходность, соединяющей точки F и S:
Е (г) =0,06 +0,40ст
где угол наклона равен 0,40. Понятно, что теперь инвестор находится в лучшем положении, потому что он может достичь более высокой ожидаемой ставки доходности для любого уровня риска, на который он готов пойти.

12.3.3. Формирование наиболее предпочтительного инвестиционного портфеля

Чтобы завершить анализ, давайте рассмотрим выбор инвестора с точки зрения его предпочтений и с учетом графика соотношения риск/доходность для эффективных портфелей. Надеюсь, вы не забыли, что в разделе 12.1 мы упоминали о том, что предпочтения при формировании портфеля зависят от стадии жизненного цикла, на которой находится инвестор, периода (горизонта) планирования и толерантности к риску. Следовательно, инвестор может выбрать позицию в любой точке на отрезке, ограниченном точками F и Г. На рис. 12.5 для этого выбрана точка Е. Портфель, который соответствует точке Е, на 50% состоит из портфельных инвестиций в общей точке (тангенциальный портфель) и на 50% из инвестиций в безрисковый актив. Преобразуем уравнения 12.1 и 12.2 таким образом, чтобы они отражали тот факт, что портфель в точке касания — это теперь единственный рискованный актив, который следует объединять с безрисковым активом. Выясняется, что ожидаемая доходность и стандартное отклонение портфеля Е имеют вид:
() = /у + 0,5 х [?(/y) - /7] = 0,06 + 0,5(0,122 - 0,06) = 0,091 ст= 0,5ха,- =0,5х0,146=0.073
Учитывая, что тангенциальный портфель состоит на 69,2% из рискованного актива 1 и на 30,8% — из рискованного актива 2, можно определить, что состав портфеля будет следующим:

Следовательно, если вы инвестировали 100000 долл. в портфель Е, то 50000 долл. инвестировано в безрисковый актив, 34600 долл. — в рискованный актив 1 15400 долл. — в рискованный актив 2.
Давайте теперь обобщим имеющиеся у нас сведения относительно создания эффективного портфеля, когда имеется два вида рискованных активов и один безрисковый актив. Существует только один портфель с рискованными активами, который оптимальным образом можно объединить с безрисковым активом. Мы называем этот особенный портфель с рискованными активами, соответствующий общей (тангенциальной) точке Г на рис. 12.4, оптимальной комбинацией рискованных активов. Предпочтительный портфель всегда является какой-либо комбинацией портфеля рискованных активов в общей точке и безрискового актива .

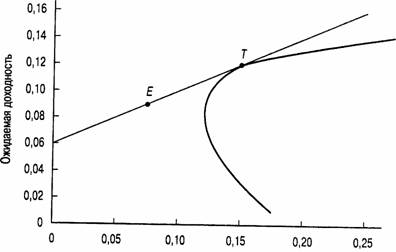
Стандартное отклонение Рис. 12.5. Выбор наиболее предпочтительного портфеля

12.3.4. Как получить заданную ожидаемую доходность: пример 2

Предположим, что у вас имеется 100000 долл., которые вы хотели бы инвестировать с ожидаемой ставкой доходности в 0,10 годовых. Сравните стандартное отклонение доходности, на которое вам пришлось бы пойти при прежнем графике риск/доходность (линия, соединяющая точки Ей S) со стандартным отклонением при новом графике риск/доходность (линия, соединяющая точки F и 7). Каков состав каждого из этих двух портфелей?
Решение
Во-первых, давайте запишем формулу, связывающую ожидаемую доходность Портфеля с долей, инвестированной в рискованные активы, и решим его. Таким обра-эом мы определим долю, которую надо инвестировать в рискованные активы. Для но-"ого соотношения риск/доходность, в котором используется оптимальная комбинация Двух рискованных активов, формула имеет следующий вид:
? (г) =?•(/,>+г, (1-w) ?(/•)= 0,122w+0,06(1-н')

Установив ожидаемую ставку доходности портфеля равной 0,10 и определив н', получим:
?(/-)=-0,06 + 0,062w =0,10
0,10-0,06 . .-
w = ————— = 0,6D 0,062
Следовательно, для получения оптимальной комбинации 65% от 100000 долл. должно быть инвестировано в рискованные активы, а 35% — в безрисковый актив. Стандартное отклонение в таком портфеле определяется по формуле:
(j=\v(t =0,65х0,146=0,095
Поскольку оптимальная комбинация рискованных активов сама по себе содержит 69,2% рискованного актива 1 и 30,8% рискованного актива 2, состав итогового портфеля с ожидаемой доходностью в 0,10 в год определяется следующим образом:

Для прежнего графика соотношения риск/доходность с единственным рискованным активом формула, связывающая ожидаемую доходность и w, имела вид:
?(r) =?(/•>+/у (1-uQ ?(r)=0,14w+0,06(l-w)
Установив ожидаемую ставку доходности портфеля равной 0,10 и вычислив w, получим:
?(r)= 0,06+0,08=0,10

Таким образом, 50% от 100000 долл. должно быть вложено в рискованный актив 1.
а 50% — в безрисковый актив.
Стандартное отклонение этого портфеля задано уравнением:

Контрольный вопрос 12.9
Предположим, инвестор выбрал портфель, который на рис. 12.5 соответствует точке, лежащей на отрезке между точками F и Т на расстоянии в три четверти длины отрезка от точки F. Другими словами, 75% его портфеля вложено в портфель, соответствующий общей точке, а 25% — в безрисковый актив. Какова ожидаемая ставка доходности и стандартное отклонение этого портфеля? Если у инвестора имеете 1000000 долл., то сколько ему следует вложить в каждый из трех активов?

Важно отметить, что при поиске оптимальной комбинации рискованных активов нам не нужно ничего знать ни о благосостоянии инвестора, ни о его предпочтениях. Состав этого портфеля зависит только от ожидаемых ставок доходности и стандартных отклонений рискованного актива 1 и рискованного актива 2 и от корреляции между ними. Это означает, что все инвесторы, которые согласились на такие характеристики доходности (среднее значение, стандартное отклонение, корреляция), захотят инвестировать в один и тот же тангенциальный портфель, дополненный безрисковым активом. Вот общее правило, применимое ко всем случаям, когда имеется множество рискованных активов:
Всегда существует оптимальный портфель рискованных активов, который все инвесторы, избегающие риска и имеющие одинаковые представления о характеристиках
доходности, будут объединять с безрисковым активом с целью получения наиболее предпочтительного портфеля.

12.3.5. Портфели с множеством рискованных активов

При наличии большого числа рискованных активов мы используем двухэтапный метод создания портфеля, аналогичный тому, который был рассмотрен в предыдущем разделе. На первом этапе мы рассматриваем портфели, состоящие только из рискованных активов, а на втором этапе мы определяем тангенциальный портфель рискованных активов, который можно объединить с безрисковым активом. Такая работа требует большого количества вычислений, поэтому лучше выполнять ее на компьютере.
На рис. 12.6 показаны исходные данные и результат их обработки в программе электронных таблиц, используемой для оптимизации портфеля7. Индивидуальные базовые активы (basic assets) — это рискованный актив 1, рискованный актив 2 и т.д. Они представлены затененными точками на диаграмме слева. Кривая, лежащая выше и правее этих точек, называется границей эффективного множества портфелей (efficient portfolio frontier) рискованных активов. Она определяется как множество портфелей с рискованными активами, каждый из которых предлагает инвесторам максимально возможные ставки доходности при любом заданном стандартном отклонении.

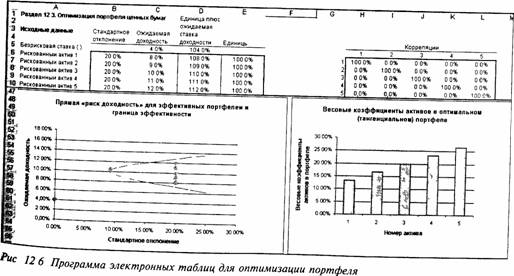
ис. 12.6 создан с помощью программного обеспечения, поставляемого с этой книгой.

Отдельные базовые активы находятся с внутренней стороны границы эффективности по той причине, что обычно существует некая комбинация из двух и более базовых активов, ожидаемая ставка доходности которой при таком же стандартном отклонении выше, чем у этих базовых активов.
Оптимальное сочетание рискованных активов обнаруживается в общей точке пересечения прямой, которая начинается в точке, представляющей безрисковый актив (на вертикальной оси), и границы эффективности рискованных активов. Отрезок, соединяющий точку безрискового актива и тангенциальную точку, которая соответствует оптимальной комбинации рискованных активов, представляет самые лучшие соотношения риск/доходность.
Теперь вернемся к вопросу, который мы уже затрагивали в разделе 12.1. Каким образом финансовый посредник (например, компания, предлагающая инвесторам инвестиции в управляемые ею взаимные фонды) составляет "финансовое меню" из разных комбинаций активов, чтобы предложить его своим клиентам? Мы только что показали, что нахождение оптимальных комбинаций рискованных активов зависит только от ожидаемого уровня доходности, стандартных отклонений базовых рискованных активов и от корреляции между ними. Оно не зависит от предпочтений инвесторов. Следовательно, для того, чтобы создать эффективный портфель, сведения о предпочтениях инвесторов совершенно не нужны.
Итак, клиенты возлагают на финансовых посредников, которые специализируются на соответствующих видах деятельности, составление прогноза ожидаемого уровня доходности активов, стандартных отклонений и корреляции; посредники берут на себя также функцию комбинирования базовых активов в оптимальных пропорциях. Следовательно, клиентам остается только выбрать размеры капиталов, которые они намерены вложить в оптимальный рискованный портфель.
Статическая модель выбора активов для инвестиционного портфеля, опирающаяся на среднее значение доходности и ее дисперсию, заложила теоретические основы финансового посредничества взаимных фондов. Начиная с конца 60-х годов академические исследования в области составления оптимального портфеля вышли за пределы этой модели и занялись динамическими версиями. В них межвременная оптимизация решений инвесторов относительно сбережения/потребления, принимаемых на определенных стадиях жизненного цикла домохозяйства, объединяется с распределением высвободившихся сбережений среди альтернативных направлений инвестиций. В этих моделях спрос на индивидуальные активы зависит от более серьезных факторов, нежели достижение оптимальной диверсификации, как было показано выше. Он является также следствием желания хеджировать различные риски, не включенные в пере-воначальную модель. В число рисков, которые создают потребность в хеджировании при принятии решений о составе портфеля, входят риск смерти, риск случайных изменений процентных ставок и ряд других. Динамические модели значительно обогатили теоретические воззрения на роль ценных бумаг и финансовых посредников при формировании инвестиционного портфеля8.
В практике управления активами в рамках инвестиционного менеджмента по-прежнему преобладает базовый метод оценки риска на основании вычисления средней доходности и дисперсии портфеля (mean-variance approach). Однако все меняется. Благодаря более совершенным моделям составления портфеля инвестиционные компании теперь могут предлагать клиентам не просто оптимальные комбинации Р1101 ванных и безрисковых активов, а целое "семейство" взаимных фондов. Эти дополн". тельные фонды позволяют создавать оптимальные хеджинговые портфели, Р041") ные на еще более полное удовлетворение запросов самых разных клиент» Инвестиционная компания может создавать из своих взаимных фондов интегрйР
'-"•''•la
8 См. R.C. Merton, Continuous-Time Finance, Blackwell, 1992, главы 4-6, 14, 15 и 21.

Цанные продукты, объединяя разные комбинации своих фондов в пропорциях, кото-|це соответствуют запросам клиентов на разных стадиях их жизненных циклов.

резюме
Не существует "единственно верной" стратегии выбора инвестиционного портфеля, которая одинаково подходила бы всем инвесторам без исключения.
Стадия жизненного цикла, на которой в данный момент находится инвестор, является важнейшим определяющим фактором при выборе оптимального состава портфеля активов и обязательств данного инвестора.
При выборе портфеля очень важен временной период. Мы различаем три вида
временных периодов — период планирования, период пересмотра решений и период биржевых торгов.
При принятии решений о составе портфеля инвестор достигнет более высокой
ожидаемой (средней) доходности, только если согласится на более высокую степень риска.
Иногда можно снизить степень риска инвестиций, не снижая ожидаемой доходности, за счет более полной диверсификации как в пределах одного класса активов, так и среди нескольких разных классов активов.
Способность за счет диверсификации снизить рискованность портфеля инвестора зависит от корреляции между активами, составляющими портфель. На практике подавляющее большинство активов имеет между собой положительную корреляцию, потому что на них влияют одни и те же экономические факторы. Следовательно, возможность снижения риска за счет диверсификации среди рискованных активов без снижения ожидаемого уровня доходности ограничена.
Несмотря на то что в принципе инвесторы при составлении портфеля могут выбирать среди тысяч разнообразных активов, на практике их "меню" ограничено несколькими продуктами, которые предлагают им финансовые посредники. К ним относятся банковские счета, взаимные фонды, состоящие из акций и облигаций, а также недвижимость. При разработке и составлении "меню" активов, предлагаемых клиентам, компании-посредники используют новейшие достижения финансовых технологий.
Основные термины
• формирование портфеля (portfolio selection), 396
• портфель с минимальной дисперсией (minimum-variance portfolio), 408
• оптимальная комбинация рискованных активов (optimal combination of risky assets), 409
• граница эффективного множества портфелей (efficient portfolio frontier), 413
1 пожизненная рента (life annuity), 397
стратегия инвестирования (investment strategy), 399
эффективный портфель (efficient I portfolio), 405

на контрольные вопросы
иьный вопрос 12.1. В чем разница между инвестиционным портфелем молодого че-с гарантированной занятостью и инвестиционным портфелем пенсионера, для 'W доход, приносимый им — это единственное средство существования?

ОТВЕТ. Молодой человек, не рискующий потерять работу, может рассчитывать на длительный период регулярного получения жалованья, размер которого, возможно будет увеличиваться с ростом инфляции. Для него инвестирование в акции не будет столь рискованным делом, как для пожилого вкладчика, который заинтересован в том, чтобы обеспечить себе стабильный источник дохода до конца жизни. Молодой человек в какой-то мере защищен от инфляции, а пожилой — нет, поэтому ем\' имеет смысл подыскать себе форму страхования от роста цен.

Контрольный вопрос 12.7. Как инвестор может получить ожидаемую ставку доходности в 0,105 годовых, вложив средства в рискованный актив 1 и безрисковый актив? Каким будет стандартное отклонение такого портфеля? Сравните это значение со стандартным отклонением рискованного актива 2. ОТВЕТ. Надо вложить 56,25% в рискованный актив, а остальное — в безрисковыи;
тогда будет достигнута ожидаемая ставка доходности, равная 0,105. Стандартное отклонение портфеля равно 0,1125 (сравните со стандартным отклонением для рискованного актива 2, которое равно 0,15).
Контрольный вопрос 12.8. Каково среднее значение доходности и ее стандартное отклонение для портфеля, который на 60% состоит из рискованного актива 1 и на 40% рискованного актива 2, если их коэффициент корреляции равен 0,1? ОТВЕТ.
Е (г)- 0,6х0,14 +0,4х0,08 =0,114 (72=(0,6)2x(0,2)2+(0,4)2x(0,15)2+2(0,6)(0,4)(0,l)(0,2)(0,15)= 0,01944
а =0,1394
Контрольный вопрос 12.9. Предположим, инвестор выбрал портфель, который на рис. 12.5 соответствует точке, лежащей на отрезке между точками F и Т на расстоянии в три четверти длины отрезка от точки F. Другими словами, 75% его портфеля вложено в портфель, соответствующий тангенциальной точке, а 25% — в безрисковый актив. Какова ожидаемая ставка доходности и стандартное отклонение этого портфеля ? Если уинвестора имеется 1000000 долл., то сколько ему следует вложить в каждый из трех активов?
ОТВЕТ.
Е (г) = 0,12154 х 0,75 + 0,06 х 0,25 = 0,1062 = 0,75 х 0,14595 = 0,1095
Надо вложить 25% в безрисковый актив, 51,9% (0,75х69,2) в рискованный актив 1, а 23,1% (0,75х30,8) — в рискованный актив 2.

. Предположим, что ваш 58-летний отец работает в RuffyStuffedToyCompany(компании, производящей игрушки) и в течение последних 15 лет регулярно делает взносы в фонд сбережений компании (company-matched savings plan). Руководство RuffyStuffedToy дополнительно добавляет в фонд сбережений 0,50 долл. к каждому 1,00 долл., которые вносит ваш отец, пока не будет достигнута сумма, равная 6% от его жалованья. Участники этого фонда могут разместить свои вклады по четырем видам инвестиций: (1) фонд облигаций с фиксированным доходом; (2) "смешанный" опцион, который инвестируется в крупные компании, мелкие компании и фонд облигаций с фиксированным доходом; (3) взаимный фонд, инвестирующий в растущие акции, при этом его средства не вкладываются в другие компании по производству игрушек; и (4) фонд, единственной инвестицией которого являются акции самой RuffyStuffedToyCompany. Когда вы приехали домой на День благодарения, ваш отец вспомнил, что вы специализируетесь на финансовых дисциплинах, и решил получить хоть какую-то отдачу от тех денег, которые он вложил в ваше образование. Он показал вам самый последний квартальный отчет по его плану сбережений, и вы увидели, что 98% его текущих вкладов находится в четвертом инвестиционном фонде — в акциях компании Ruffy.
Предположим, что ваш отец — самый обычный человек, не склонный к риску;
через пять лет он собирается выйти на пенсию. Когда вы спросили его, почему он разместил свои инвестиции именно таким образом, он ответил, что акции компании всегда котируются очень хорошо; правда, было несколько случаев, когда они падали в цене, но это было связано с проблемами в подразделениях компании, которые теперь уже проданы. Кроме того, говорит ваш отец, многие из его друзей, работающих в этой же компании, поступили так же. Какие советы вы могли бы дать отцу относительно размещения его вложений? Почему?
Учитывая тот факт, что ваш отец не только вложил в акционерный фонд Ruffy98% своих сбережений, но и работает на эту компанию, что вы можете сказать о ситуации? Есть ли тут дополнительный риск или, наоборот, можно говорить о снижении риска? Или это не имеет никакого значения? Почему? 2. См. табл. 12.1.
а. Выполните вычисления, подтверждающие, что ожидаемая доходность каждого из портфелей (F, G, И, J, S) в таблице (столбец 4) указана верно.
Ь. Выполните то же самое для стандартного отклонения в столбце 5 таблицы.
с. Предположим, у вас есть миллион долларов, который вы хотели бы инвестировать. Разместите деньги, как показано в таблице для каждого из этих портфелей, и рассчитайте ожидаемый уровень доходности (в долларах) для каждого из портфелей.
d. Который из портфелей мог бы выбрать инвестор с очень высокой толерантностью к риску?
3. Компания, управляющая взаимными фондами, предлагает вложить деньги в безрисковый фонд денежного рынка (фонд, инвестирующий в высоколиквидные краткосрочные ценные бумаги — Прим. ред.}, чья ставка доходности равна сегодня 4,50% (0,045). Та же компания предлагает также акции взаимного фонда, нацеленного на агрессивный рост (инвестиционный фонд, пытающийся обеспечить максимальную долгосрочную прибыль от акций мелких компаний и узких секторов рынка — Прим. ред.), который на протяжении ряда лет показывает средний уровень доходности в 20% (0,20) и стандартное отклонение в 0,25.
а. Выведите уравнение для графика, показывающего соотношение риск/доходность.
Ь. Какова дополнительная доходность, которую сможет получить инвестор на каждую дополнительную единицу риска, на которую он согласится?
с. Каким должно быть размещение инвестиций в фонде денежного рынка, если инвестор рассчитывает на ожидаемую доходность в 15% (0,15)?
4. Если график соотношения риск/доходность для безрискового и рискованного активов имеет отрицательный наклон, что можно сказать о соотношении рискованного и безрискового активов?
5. Предположим, что у вас есть возможность купить акции AT&Tи Microsoft. Доходность AT&TMicrosoftСреднее значение 0,10 0,21 Стандартное отклонение 0,15 0,25
а. Как получить портфель с минимальным риском (минимальной дисперсией), состоящий из акций корпораций А Т& Т и Microsoft, если корреляция между двумя акциями равна О? 0,5? I? -1? Что можно сказать об изменении пропорции капиталов, вложенных А Т&Т и Microsoft, по мере того, как их корреляция меняется от -1 до 0, затем до 0,5, затем до +1? Почему это происходит?
Ь. Какова дисперсия каждого портфеля с минимальной дисперсией в вопросе 5д?
с. Какова оптимальная комбинация этих двух акций в портфеле для каждого из значений корреляции с учетом существования фонда денежного рынка с сегодняшней процентной ставкой 4,50% (0,045)? Заметили ли вы какое-либо соотношение между их весами и весами для портфелей с минимальной дисперсией?
d. Какова дисперсия каждого из оптимальных портфелей?
е. Каков ожидаемый уровень доходности каждого из оптимальных портфелей.
f. Выведите график соотношения риск/доходность для оптимального портфеля при корреляции, равной 0,5. На какую дополнительную доходность вы можете рассчитывать, если согласитесь на дополнительный риск?
6. Используя оптимальный портфель, состоящий из акций AT&Tu. Microsoft, когда коэффициент корреляции динамики их курсов равен 0,5, а также результаты части 1 вопроса 12.6, выполните следующие действия.
а. Определите ожидаемую доходность и стандартное отклонение портфеля, к торый на 100% состоит из инвестиций в фонд денежного рынка с текущей процентной ставкой 4,5%. Где находится соответствующая ему точка на прямой соотношения риск/доходность?
Ь. Определите ожидаемую доходность и стандартное отклонение портфеля, который на 90% состоит из инвестиций в фонд денежного рынка и на 10% — в портфель с акциями корпораций А Т& Т и Microsoft.
с. Определите ожидаемую доходность и стандартное отклонение портфеля, который на 25% состоит из инвестиций в фонд денежного рынка и на 75% — в портфель с акциями корпораций ат&ти Microsoft.
d. Определите ожидаемую доходность и стандартное отклонение портфеля, который на 0% состоит из инвестиций в фонд денежного рынка и на 100% — в портфель с акциями корпораций AT&Tи Microsoft. Где лежит соответствующая ему точка?
7. Опять же, используя оптимальный портфель акций AT&T и Microsoft, когда корреляция динамики их цен равна 0,5, возьмите 10000 долл. и определите их размещение среди безрискового актива, акций ат&ти акций Microsoft.
а. для портфеля, который на 75% состоит из инвестиций в фонд денежного рынка и на 25% — из инвестиций в портфель с акциями AT&T и Microsoft. Каков ожидаемый уровень доходности этого портфеля?
Ь. для портфеля, который на 25% состоит из инвестиций в фонд денежного рынка и на 75% — из инвестиций в портфель с акциями AT&T и Microsoft. Каков ожидаемый уровень доходности этого портфеля?
с. для портфеля, который не содержит инвестиций в фонд денежного рынка и на 100% состоит из инвестиций в акции ат&ти Microsoft. Каков ожидаемый уровень доходности этого портфеля?
8. Какая стратегия должна использоваться при движении вправо по прямой, показывающей соотношение риск/доходность, от тангенциальной точки, где эта прямая соприкасается с кривой риск/доходность для рискованных активов? Инвесторы какого типа скорее всего согласятся на такую стратегию? Почему?
9. Определите корреляцию между динамикой цен на акции А и В с помощью прогнозов их ставок доходности и оценок возможных состояний экономики на основании следующей таблицы. Стандартные отклонения для акций А и В равны соответственно 0,065 и 0,1392. Прежде чем приниматься за расчеты, попробуйте, взглянув на данные, определить, к какому значению будет ближе корреляция — к 1 или к -1.

10. Проанализируйте ответы "эксперта" на следующие вопросы.
а. Вопрос. Примерно треть моих инвестиций вложена в акции и в инструменты денежного рынка. Можете ли вы посоветовать какое-нибудь безопасное вложение для второй трети моих денег? Одну треть я хотел бы на всякий случай иметь под рукой.
Ь. Ответ эксперта. Можете попробовать годовые и двухлетние облигации Казначейства США. Вы получите немного большую доходность, а риска никакого.
с Вопрос. Куда вы вложили бы свои деньги, если представилась возможност начать все сегодня9
d Ответ эксперта. Это зависит от возраста и ближайших целей Если вы мопо ды — скажем, вам еще нет 40, и вам не нужны деньги на обучение или noicvn ку дома, то я рекомендовал бы вложить в инвестиционный фонд, активы кп торого состоят преимущественно из акций Даже есто рынок б>дет не\стои-чив, у вас будет время компенсировать потери До настоящего времени течении 10 лет доходность никакого из финансовых инструментов не превысила доходность акций Но если деньги понадобятся вам довольно скоро пример на покупку дома или к выходу на пенсию, следует быть осторожнее
Краткий обзор формул
Ожидаемая (средняя) ставка доходности любого портфеля, Ь(г), определяется формулой
где w — это доля портфеля, инвестированная в рискованный актив, Ь(г} — ожидаемая доходность рискованного актива, а л/г — ставка доходности для безрисковых активов
Стандартное отклонение портфеля определяется по формуле а = a,\v
где о, — это стандартное отклонение доходности рискованного актива
Формула для графика, описывающего соотношение между риском и ожидаемой доходностью, имеет вид
Формула для дисперсии портфеля двух рискованных активов такова ст2 = но-2 + (1 - w)2 (Т2 + 2w (1 - w) po-iO-;,

Формула для определения пропорций оптимальной комбинации двух рискованных активов выглядит следующим образом

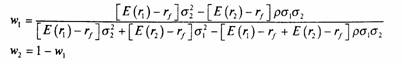
ПРИЛОЖЕНИЕ
Заблуждения относительно влияния фактора времени на диверсификацию активов
Существует широко распространенное — хотя и ошибочное — мнение, что риск, связанный с инвестициями в акции, снижается с увеличением срока владения ими Из этого убеждения следует общей вывод чем дольше вы собираетесь владеть акциями, тем больше денег следует в них вкладывать

Для убеждения скептиков в том, что так называемый "эффект времени в диверсификации" действительно имеет место, существует два доказательства
• Чем дольше период, в течение которого инвестор собирается владеть акциями, тем меньше стандартное отклонение доходности акций, взятое в годовом исчислении
• Чем дольше период, в течение которого инвестор собирается владеть акциями, тем меньше вероятность того, что ставка доходности акций окажется ниже соответствующей процентной ставки для безрисковых облигаций
Эти доказательства, хотя и верны по сути, не являются убедительной аргументацией для утверждения о том, что акции — это менее рискованные активы, если владеть ими в течение длительного времени, или что вам следует больше инвестировать в акции, потому что вы предполагаете вкладывать средства на длительный срок Сейчас объясним, почему
Во-первых, тот факт, что стандартное отклонение ставки доходности акций, приведенной к годовому исчислению, уменьшается по мере увеличения периода владения ими, является просто артефактом, следующим из применяемой методики ее исчисления В такой ситуации нет подлинной диверсификации Дело в том, что не уменьшается стандартное отклонение вашего богатства, которое вы будете иметь к концу периода владения акциями Сравните, например, результаты инвестирования в акции и в безрисковые облигации сроком на один год и на 25 лет Пусть даже стандартное отклонение вашей ставки доходности (приведенной к годовому исчислению) для 25-летнего периода составляет приблизительно одну пятую по сравнению с ее значением для годичного периода Все равно стандартное отклонение вашего итогового уровня благосостояния по истечении 25-летнего периода владения акциями в пять раз больше, чем стандартное отклонение для года
Во-вторых, верно, что чем дольше период владения акциями, тем меньше вероятность дефицита {shortfall) Этот термин означает, что доходность портфеля акций меньше, чем процентная ставка безрисковых активов за тот же период Однако риск дефицита зависит от того, насколько этот дефицит, если он возникнет, серьезен, а также от вероятности его наступления Если мы рассматриваем систему измерения риска, при которой учитываются и серьезность, и вероятность дефицита, то с увеличением срока владения этот риск не уменьшается Например, если считать мерой риска цену страховки портфеля инвестиции от дефицита, то эта цена увеличивается вместе с продолжительностью владения акциями9

Ваш комментарий о книге
Обратно в раздел Экономика и менеджмент