Боди З., Мертон Р. Финансы

ОГЛАВЛЕНИЕ

Глава 8 ОЦЕНКА АКТИВОВ С ФИКСИРОВАННЫМИ ДОХОДАМИ: ОБЛИГАЦИИ

В этой главе...
• Оценка финансовых контрактов и ценных бумаг с фиксированными доходами
• Анализ изменения цен и доходности по облигациям с течением времени

Содержание
8.1. Оценка инструментов с фиксированными доходами на основании расчета приведенной стоимости
8.2. Основные инструменты анализа: бескупонные облигации
8.3. Купонные облигации, текущая доходность и доходность при погашении % 8.4. Чтение таблиц котировки облигаций
8.5. Почему ценные бумаги с одинаковыми сроками погашения могут иметь различную доходность
8.6. Время и динамика цен облигаций

В главе 7 было показано, что сущность процесса оценки активов заключается в определении их рыночной стоимости на основе информации о ценах на сопоставимые активы и выполнения соответствующих корректировок с учетом имеющихся различий. В модели стоимостной оценки активов для определения их стоимости (информация, получаемая на выходе модели) используются специальные формулы,которые вводится рыночная информация о ценах на сопоставимые активы и о процентных ставках (входящая информация).
В этой главе будет рассмотрена оценка ценных бумаг с фиксированным доходом других финансовых инструментов с заведомо известными потоками будущих платежей. Примерами подобных активов могут служить такие ценные бумаги с фиксированным доходом, как облигации, пожизненные аннуитеты или контракты типа ипотечных. Такие ценные бумаги и договора очень важны для домохозяйств, та именно они являются главными источниками доходов для финансирования покупкисобственных домов и приобретения потребительских товаров длительного пользования. Они также представляют большую ценность как для частных фирм, так иправительства (федерального и штатных) в качестве надежных источников денежных средств.
Наличие модели оценки таких активов очень важно, по крайней мере, по двум причинам. Первая заключается в том, что сторонам, заключающим финансовый тракт, необходимо в самом начале иметь взаимосогласованную процедуру оценки его условий. Вторая причина связана с тем, что ценные бумаги с фиксированным доходом часто продаются до наступления срока их погашения. В связи с тем, что на их стоимость влияет рыночная ситуация, а именно изменение процентных ставок с течением времени, покупателям и продавцам необходимо каждый раз переоценивать данные финансовые активы.
Для определения стоимости ожидаемых денежных потоков в разделе 8.1 рассматривается основная модель стоимостной оценки, использующая формулу расчета чистой приведенной стоимости по единой дисконтной ставке. В разделе 8.2 рассматривается корректировка этой модели с учетом того, что в реальной схеме кривая доходности не является постоянной (т.е. уровень доходности облигаций меняется в зависимости от срока погашения). В разделах 8.3-8.5 описываются характерные особенности облигаций и то, как они влияют на их цену и доходность в реальном финансовом мире. В разделе 8.6 рассматривается, как изменения в процентных ставках отражаются на рыночной цене облигаций.

8.1. ОЦЕНКА ИНСТРУМЕНТОВ С ФИКСИРОВАННЫМИ ДОХОДАМИ НА ОСНОВАНИИ РАСЧЕТА ПРИВЕДЕННОЙ СТОИМОСТИ

В главе 4 описано, что если существует единственная безрисковая (ее также называют гарантированной, или надежной) процентная ставка, расчет приведенной стоимости любого потока ожидаемых денежных поступлений не представляет особой сложности. Эта задача включает в себя применение формулы расчета чистой приведенной стоимости с использованием безрисковой процентной ставки в качестве ставки дисконтирования.
Предположим, что вы приобрели ценную бумагу с фиксированным доходом с ежегодной выплатой по ней 100 долл. на протяжении последующих трех лет. Какова стоимость этого трехлетнего финансового контракта типа аннуитета, если известно, что соответствующая дисконтная ставка составляет 6% в год? Как показано в главе 4, ответ будет равен 267,30 долл. и может быть легко получен с помощью специального финансового калькулятора, таблицы, в которой указаны коэффициенты приведенной стоимости или с помощью математической формулы.
Напомним формулу для расчета приведенной стоимости обычного аннуитета, равного 1 долл. для периодов, при процентной ставке (i):

В финансовый калькулятор введем значения для и, (", РМТ и рассчитаем приведенную стоимость (PV):

Теперь предположим, что через час после покупки этой ценной бумаги вам необходимо ее продать, но за это время безрисковая процентная ставка поднялась с 6% до %в год. Сколько теперь можно получить за нее?
Уровень процентных ставок изменился, но ожидаемые денежные поступления от инвестиций в данную ценную бумагу остались неизменными. Для того чтобы инвестор смог получить 7% доходности в год, цена этого актива должна понизиться. Насколько? До той отметки, при которой она будет равна приведенной стоимости ожидаемых денежных потоков, дисконтированных по 7%-ной ставке.

Ценная бумага с фиксированным доходом с ежегодной выплатой по ней 100 долл. на протяжении последующих трех лет имеет приведенную стоимость 262,43 долл. и обеспечивает своему владельцу доходность в размере 7% в год. Таким образом, при повышении рыночных процентных ставок курс любых ценных бумаг с фиксированным доходом понижается. Это связано с тем, что инвесторы приобретут только в том случае, если они обеспечат им уровень доходности, соответствующий новым рыночным условиям.
Итак, повышение процентной ставки на 1% приведет к падению курса ценной бумаги на 4,87 долл. И наоборот, понижение процентной ставки приведет к соответствующему повышению ее курса.
Это иллюстрирует основной принцип, используемый при оценке активов с заведомо известными, фиксированными денежными потоками. Изменение рыночных процентных ставок приводит к изменению в противоположном направлении рыночных цен всех имеющихся финансовых контрактов с фиксированными поступлениями платежей.
Поскольку процесс изменения процентных ставок непредсказуем, то и курс ценных бумаг с фиксированным доходом непредсказуем вплоть до момента их погашения.

На практике оценка стоимости известных денежных потоков не всегда так проста, как в приведенном примере. Это связано с тем, что в реальной жизни обычно неизвестно, какую именно дисконтную ставку следует использовать в формуле вычисления, приведенной стоимости денежных поступлений. Как было отмечено в главе 2, рыночные процентные ставки различаются в зависимости от сроков погашения финансовых инструментов. На рис. 8.1 представлен график, отображающий кривую доходности (зависимость между доходностью облигаций примерно одинакового инвестиционного качества и сроками их погашения. — Прим. ред.) по облигациям Казначейства США.
Было бы заманчиво предположить, что для оценки трехлетнего аннуитета, рассматриваемого в нашем примере, в качестве дисконтной ставки может быть применена процентная ставка по облигациям Казначейства США со сроком погашения 3 года. Однако это было бы неправильно. Реальная процедура, позволяющая выполнять оценку других известных денежных потоков на основании информации, содержащейся в кривой доходности, намного более сложна.

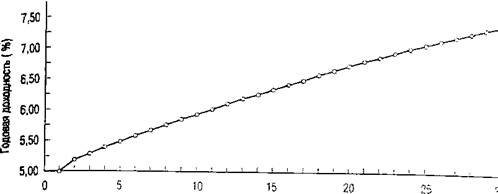
Срок до погашения (лет) Источник. The Wall Street Journal, April 3, p.C21
Рис. 8.1. Кривая доходности ценных бумаг Казначейства США

8.2. ОСНОВНЫЕ ИНСТРУМЕНТЫ АНАЛИЗА: БЕСКУПОННЫЕ ОБЛИГАЦИИ

При оценке контрактов с фиксированными доходами лучше всего начать с рас смотрения рыночных цен на бескупонные облигации, или облигации с нулевым купоне;
(pure discount bonds или zero-coupon bonds). Это такие облигации, выплата по коте рым производится только один раз, в день их погашения. День выплаты называете днем погашения облигации.
Бескупонные облигации — один из основных финансовых инструментов при оценке всех контрактов с фиксированными доходами. Объясняется это тем, что любой контракт всегда можно разложить на составляющие его компоненты — денежные потоки, — после чего проанализировать в отдельности все ожидаемые по контракт денежные потоки и затем просуммировать их.
Ожидаемая сумма платежа по бескупонной облигации называется ее номинальной или нарицательной стоимостью (face value, или par value). Доход, полученный инвестором по бескупонной облигации в день погашения, представляет собой разницу между ценой приобретения облигации и ее номиналом. Таким образом, бескупонная облигация со сроком погашения через один год, имеющая номинальную стоимостью 1000 долл. и цену приобретения 950 долл., принесет доход в размере 50 долл.
Доходность (yield) бескупонной облигации — это годовая ставка доходности, полу чаемая инвестором, купившим и владеющим данной облигацией до момента ее погашения1. Для бескупонной облигации со сроком погашения через 1 год (как в HaineN примере) доходность составляет:

Доходность 1 - годичной бескупонной облигации

=0,0526 или 5,26 %

Однако, если срок погашения облигаций отличен от одного года, то для того чтобы определить доходность по таким облигациям, следует использовать формулу приведенной стоимости. Рассмотрим бескупонную облигацию со сроком погашения через 2 года номинальная стоимость которой 1000 долл., а покупная цена 880 долл. Расчет годовой доходности по такой облигации следует производить как расчет дисконтной ставки которая приравняет ее номинальную стоимость с ее покупной ценой. В финансовом калькуляторе введем значения для параметров п, PV, FVn рассчитаем значение (i).

Вернемся к оценке ценной бумаги, которая рассматривалась в разделе 8.1. (срок погашения 3 года с ежегодной выплатой 100 долл.). В табл. 8.1 представлены цены на бескупонные облигации. Следуя обычной практике, цена на облигацию приводится в качестве составляющей части от ее номинальной стоимости (курс облигации).

Таблица 8.1. Цены бескупонных облигаций и их доходность

Для расчета стоимости данной ценной бумаги существует два варианта. В первом используются значения из второго столбца табл. 8.1, а во втором — доходность из последнего столбца. Таким образом, в первом варианте каждый из трех ожидаемых платежей умножается на соответствующее ему значение, которое представляет собой цену за 1 долл. от номинальной стоимости облигации. Затем все результаты суммируются.
Приведенная стоимость ожидаемых поступлений за 1-й год = 100 долл. х 0,95 =
95 долл.
Приведенная стоимость ожидаемых поступлений за 2-й год = 100 долл. х 0,88 =
88 долл.
Приведенная стоимость ожидаемых поступлений за 3-й год == 100 долл. х 0,80 =
80 долл.
Суммарная величина приведенной стоимости = 263 долл. Таким образом стоимость облигации должна составлять 263 долл. Второй вариант расчета даст точно такой же результат посредством дисконтирования каждого ожидаемого платежа по ставке доходности, соответствующей его сроку погашения.
Приведенная стоимость ожидаемых поступлений за 1-й год = 100 долл. / 1,0526 = 95,00 долл. д Приведенная стоимость ожидаемых поступлений за 2-й год = 100 долл. / 1,06602 = 88,00 долл. Приведенная стоимость ожидаемых поступлений за 3-й год = 100 долл. / 1,07723 = 80,00 долл.
Суммарная величина приведенной стоимости составляет 263 долл. Заметьте, однако, что было бы ошибочно дисконтировать все три ожидаемых Денежных потока по одной и той же годовой процентной ставке 7,72%, отмеченной последней строке табл. 8.1. Если бы это было так, то стоимость составили 259 долл., что на 4 долл. меньше реальной приведенной стоимости.

Существует ли единая ставка, которую можно было бы использовать для дисконтирования всех трех платежей для того, чтобы получить стоимость, равную 263 долл.? Да, единая дисконтная ставка составляет 6,88% за 1 год. Для того чтобы убедиться в этом, подставим в таблицу в качестве (i) значение 6,88%

Проблема заключается в том, что дисконтная ставка 6,88%, подходящая для оценки стоимости трехгодичного аннуитета, нигде в табл. 8.1не отражена. Мы получили это значение исходя из того, что нам было известно, что стоимость ценной бумаги должна составлять 263 долл. Иначе говоря, для того, чтобы найти (I), необходимо использовать формулу расчета приведенной стоимости.

Но задача заключалась именно в том, чтобы определить значение приведенной стоимости (т.е. 263 долл.). Таким образом, не существует прямого способа оценки стоимости трехгодичного аннуитета исходя из единой дисконтной ставки и данных, представленных в табл. 8.1.
Подытоживая этот раздел, можно прийти к следующему выводу. Если кривая доходности не является параллельной оси ОХ (т.е. если рассматриваемые ставки доходности не являются одинаковыми для всех сроков погашения), то правильная процедура для оценки стоимости контракта или ценной бумаги с фиксированными потоками денежных платежей заключается в следующем: необходимо дисконтировать каждый ожидаемый платеж по ставке доходности, соответствующей бескупонной облигации с соответствующим сроком погашения, а затем просуммировать все полученные результаты.

8.3. КУПОННЫЕ ОБЛИГАЦИИ, ТЕКУЩАЯ ДОХОДНОСТЬ И ДОХОДНОСТЬ ПРИ ПОГАШЕНИИ

Купонная, или процентная облигация (coupon bond) обязывает ее эмитента осуществлять периодические выплаты процентов, называемые купонными платежами, держателю облигации на протяжении срока ее обращения, а затем выплатить на дату погашения номинальную стоимость облигации (т.е. на день выплаты последнего процентного дохода). Периодические выплаты процентов называются купонными платежами (couponpayments). Это связано с тем, что такие облигации имеют купоны, которые отрезаются по мере наступления срока платежей и предъявляются эмитенту для получения процентов.
Купонная доходность (coupon rate) — это процентная ставка доходности относительно номинала облигации, используемая для расчета купонных платежей. Поэтому облигация номиналом 1000 долл. и купонной доходностью 10% обязывает эмитента выплачивать ее владельцу каждый год 0,10 х 1000 долл., т.е. 100 долл. Если срок погашения облигации составляет 6 лет, то по окончании шестого года эмитент произведет оплату последнего купона — 100 долл. — и выплатит номинальную стоимость облигации — 1000 долл2.
Поток денежных платежей по такой облигации представлен на рис 8.2. Видно, что ожидаемые денежные потоки представлены компонентами аннуитета (фиксированными во времени платежами) в размере 100 долл. в год и единовременной выплатой номинальной стоимости облигации 1000 долл. в момент ее погашения (так называемый платеж типа "воздушного шара" или "пули"). Купонные платежи в размере 100 долл. определяются на момент выпуска облигации и остаются неизменными вплоть до срока погашения. В день выпуска облигации ее цена обычно равна 1000 долл. (т.е. ее номинальной стоимости).

Рис. 8.2. Денежные потоки для 10%-ной купонной облигации номиналом 1000 долл.

Связь между ценами и доходностью для купонной облигации более сложна, чем для бескупонной. Далее будет показано, что если цены купонных облигаций отклоняются от их номинальной стоимости, то само понятие "доходность" приобретает нечеткое толкование.
Купонные облигации с рыночной ценой, совпадающей с их номинальной стоимости, называются облигациями, котирующимися по номиналу (par bonds). Если рыночная цена купонной облигации соответствует ее номинальной стоимости, то доходность по такой облигации равна купонной доходности по ней. Рассмотрим, например, облигацию с номинальной стоимостью 1000 долл., срок погашения которой наступает через один год и по которой купонный платеж выплачивается из расчета 10% от номинала. Ровно через год по этой облигации будет выплачено 1100 долл.: 100 долл. в качестве купонного платежа и 1000 долл. из расчета ее номинальной стоимости. Таким образом, если текущая цена 10%-ной купонной облигации равна 1000 долл., то доходность по ней — 10%.
Первое правило оценки облигаций: номинальные облигации
Если цена приобретения купонной облигации соответствует ее номинальной стоимости, то доходность по такой облигации равна ее купонной доходности.
Часто бывает, что рыночная цена купонной облигации отличается от ее номинальной стоимости. Такая ситуация может возникнуть, например, если после того, как облигация была выпущена, уровень процентных ставок в экономике начал понижаться. Допустим, что наша 10%-ная купонная облигация была выпущена 19 лет тому назад как облигация со сроком погашения через 20 лет. В то время на кривой доходности облигации аналогичного инвестиционного качества и со сроком погашения 1 год рз полагались на уровне доходности 10% в год. Сейчас до окончания срока погашения остался один год, но теперь процентная ставка по аналогичным годовым облигациям составляет 5%.
Хотя 10%-ная купонная облигация была выпущена по номиналу (1000 долл.), ее сегодняшняя рыночная цена составляет 1047,62. В связи с тем, что цена облигации теперь превышает ее номинальную стоимость, она называется облигацией с премией (премиальной облигацией) (premium bond).
Какова доходность такой облигации?
Существует два различных показателя доходности, которые можно рассчитать. Первый — это текущая доходность (current yield), которая рассчитывается путем деления суммы платежа по годовому купону на рыночную цену облигации:

Текущая доходность= Купон / Цена = 100/1047,62 = 9,55%

Текущая доходность превышает действительную доходность премиальной облигации. Это связано с тем, что не учитывается тот факт, что на момент погашения будет выплачено только 1000 долл., т.е. на 47,62 долл. меньше, чем было заплачено за облигацию.
Для того чтобы принять во внимание тот факт, что номинальная стоимость облигации может отличаться от ее рыночной цены, рассчитаем доходность, называемую доходностью при погашении (yield-to-maturity). Доходность при погашении (ее еще называют доходностью к погашению и полной доходностью) можно рассматривать как дисконтную ставку, при которой приведенная стоимость ожидаемых денежных платежей по облигации равнялась бы ее текущей цене.
Доходность при погашении учитывает все денежные платежи, которые получит владелец облигации, включая номинальную стоимость облигации на момент ее погашения (1000 долл.). В данном случае, в связи с тем, что срок погашения облигации наступает через один год, расчет доходности при погашении не представляет особой сложности:

Доходность при погашении = (Купон + Номинал - Текущая цена) / Текущая цена

Доходность при погашении
= (100 долл. + 1000 долл. – 1047,62 долл.) / 1047,62 долл. = 5%

Таким образом, если бы при расчете ставки доходности, на которую рассчитывает покупатель облигации, использовался показатель текущий доходности (9,55%), то это привело бы к серьезным заблуждениям.
Если срок погашения облигации превышает один год, то расчет ее доходности при погашении намного более сложен, чем в предыдущем примере. Предположим, что вы Рассматриваете возможность покупки двухгодичной 10%-ной купонной облигации, имеющую номинальную стоимость 1000 долл. и текущую цену 1100 долл. Какова ее Доходность?
Ее текущая доходность равняется 9,09%.

Текущая доходность = Купон / Цена = 100 долл. / 1000 долл. = 9,09%

Однако, так же как и в случае с годичной премиальной облигацией, показатель текущей доходности не учитывает того, что на момент погашения вы получите меньше, чем платили (1100 долл.). В ситуации, когда время до погашения облигации превышает один год, доходность при погашении представляет собой ставку дисконтирования, при которой приведенная стоимость ожидаемых денежных поступлений равнялась бы текущей цене облигации.

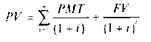
где n - количество ежегодных платежных периодов до момента погашения облигации, i — годовая доходность при погашении, РМТ' — купонный платеж, FV— номинальная стоимость облигации.
Доходность при погашении по купонной облигации с периодом погашения свыше одного года может быть вычислена с помощью специализированного калькулятора с финансовыми функциями, в который необходимо ввести следующие значения: п — количество ежегодных платежных периодов до момента погашения облигации, PV— цена облигации (со знаком "минус"), FV— ее номинальная стоимость, РМТ -— купонный платеж по облигации.

Таким образом, доходность при погашении по этой двухгодичной премиальной облигации значительно меньше текущей доходности.
Данный пример иллюстрирует основное правило, описывающее отношение между ценами облигаций и их доходностью.
Второе правило оценки облигаций: премиальные облигации
Если цена купонной облигации превышает ее номинал, то доходность при погашении по такой облигации меньше текущей доходности, которая, в свою очередь, меньше ее купонной доходности.
Соотношение ставок доходности для премиальных облигаций
Доходность при погашении < Текущая доходность < Купонная доходность
Рассмотрим теперь облигацию с 4%-ной купонной доходностью и 2-х годичным сроком погашения. Предположим, что ее цена составляет 950 долл. Вследствие того что ее рыночная цена меньше номинальной стоимости, такая облигация называется дисконтной. (Заметьте, что она отличается от бескупонной дисконтной облигация, так как по ней выплачиваются купонные платежи.)
Какова доходность такой облигации? Так же как и в предыдущем примере, можно рассчитать два различных показателя доходности: текущую доходность и доходность при погашении.

Текущая доходность = Купон / Цена = 40 долл. / 950 долл. = 4,21%

В случае с дисконтной облигацией текущая доходность по сравнению с действительной доходностью занижена. Это связано с тем, что текущая доходность не учитывает того, что на момент погашения будет выплачена большая сумма, чем та, которая была заплачена за облигацию. При погашении дисконтной облигации владелец получит 1000 долл. по номинальной стоимости облигации, а не 950 долл., которые он за нее заплатил.
Доходность при погашении учитывает все денежные платежи, которые получит владелец облигации, включая номинальную стоимость облигации на момент ее погашения (1000 долл.). С помощью финансового калькулятора можно определить значение доходности при погашении:

Таким образом, доходность при погашении этой дисконтной облигации превышает текушУ10 доходность по ней.
Третье правило оценки облигаций: дисконтные облигации
Если цена купонной облигации меньше ее номинальной стоимости, то доходность при погашении такой облигации больше текущей доходности, которая, в свою очередь, больше ее купонной доходности.
Соотношения процентных ставок для дисконтных облигаций
Доходность при погашении > Текущая доходность > Купонная доходность

8.3.1. Что нужно знать о фондах, оперирующих с "высокодоходными" облигациями Казначейства США

В прошлом некоторые инвестиционные компании, которые занимались инвестированием только в облигации Казначейства США, привлекли к себе внимание тем, что предложили такие ставки доходности, которые значительно превосходили процентные ставки по любым другим инвестиционным инструментам с таким же сроком погашения. Предлагаемая ими процентная ставка, являлась текущей доходностью, а облигации, в которые они инвестировали средства, являлись премиальными облигациями, по которым начисляются сравнительно высокие ставки купонной доходности. Поэтому в соответствии со вторым правилом оценки облигаций, фактическая ожидаемая доходность будет значительно меньше, чем рекламируемая текущая доходность.
Предположим, что вы располагаете суммой в 10000 долл., которую намереваетесь инвестировать сроком на один год. Вы стоите перед выбором, купить ли депозитный сертификат коммерческого банка, застрахованный Федеральной корпорацией страхования депозитов, или купить акции фонда, проводящего операции с облигациями Казначейства США со сроком погашения через один год. В первом случае процентная ставка составит 5%, а во втором купонная доходность — 8%. Облигации, находящиеся в активах облигационного фонда, продаются выше номинала. За каждые 10000 долл. номинальной стоимости, которые вы получите на момент погашения (через год), сейчас необходимо заплатить 10285,71. Текущая доходность фонда составляет 800 долл./10285,71 долл., или 7,78% — это и есть рекламируемая процентная ставка. Если годовые выплаты за услуги фонда составят 1%, какую фактическую доходность вы получите?
При отсутствии дополнительных затрат, связанных с вложениями в облигационный фонд, годовая ставка доходности составила бы 5%. Точно такую же ставку доходности обеспечивают и вложения в депозитные сертификаты. Это связано с тем, что покупка на 10000 долл. акций облигационного фонда даст ту же самую доходность, что и покупка 8%-ной купонной облигации с номинальной стоимостью 10000 долл. по цене 10 285,71 долл.:

Ставка доходности = (Купон + Номинал – Цена) / Цена
= (800 долл. +10000 долл. - 10285,71 долл. )/ 10286 долл. = 5%

В связи с необходимостью оплаты услуг фонда в размере 1% от 10000 долл. ваша ' ская доходность составит всего лишь 4%, а не 5%, которые предлагаются банком по его депозитным сертификатам.

8.4. ЧТЕНИЕ ТАБЛИЦ КОТИРОВКИ ОБЛИГАЦИЙ

Рабочая книга M 8.4
Цены на облигации доступны из множества информационных источников. Для инвесторов и финансовых аналитиков, нуждающихся в поминутно обновляющейся информации, наилучшим источником данных являются информационные службы, ежеминутно предоставляющие свежие данные непосредственно на их компьютеры. Те же, кто не нуждается в такой высокой оперативности, могут воспользоваться финансовой прессой, публикующей ежедневные котировки ценных бумаг.
В табл. 8.2 частично приведен курсовой бюллетень на 23 августа 1998 г. из TheWallStreetJournal, содержащий сведения о торговле как облигациями, эмитированными Казначейством США, так и отдельно оторванными от них купонами. Облигации Казначейства США с оторванными купонами и сами эти купоны (так называемые казначейские стрипы (U.S. Treasury strips)) образуются следующим образом: купонные облигации Казначейства США покупаются отдельными фирмами, которые затем в качестве самостоятельных ценных бумаг перепродают отдельно каждый купонный платеж и отдельно обязательства по погашению номинальной стоимости облигации. (Этот процесс называется отрывом купонов (couponstripping)).
Для интерпретации приведенных в бюллетене цен, необходимо ознакомиться с условными обозначениями.
1. Второй столбец таблицы (Type) указывает на первооснову платежа по казначейскому стрипу, получающегося в ходе отрыва (отделения) купонов: с;— купонный платеж, bid — номинальная стоимость облигации Казначейства США (срок погашения 10 лет и более), пр — номинальная стоимость ноты (среднесрочная облигация) Казначейства США (срок погашения 10 лет и менее).
2. Theaskprice — цена, по которой дилеры по долгосрочным облигациям хотят продавать (цена предложения), a bidprice — цена, по которой они хотят покупать (цена спроса). Цена спроса всегда превышает цену предложения. Эту разницу фактически составляют дилерские комиссионные. Ask Bid. в последнем столбце — доходность при погашении, вычисленная из расчета цены предложения. Предполагается полугодовой период начисления процентов.

Таблица 8.2. Котировка ценных бумаг Казначейства США с отделенными купонами J

Примечания
Котировка казначейских стрипов на 15.00 Восточного времени дается по операциям свыше 1000000 долл. Значения в столбцах с ценами спроса и предложения указаны в 32-х долях (32 nds); 101 01 означает 101 и 1/32. Чистые изменения также указываются в 32 nds. Доходность к погашению рассчитана исходя из цены спроса.
ci— отделенный купонный платеж;
bp — номинальный платеж по облигации Казначейства США (без купонов);
пр — номинальный платеж по ноте Казначейства США (без купонов). Источник Bear, Steams & Со. Via Street Software Technology Inc.

Таблица 8.3. Котировка облигаций Казначейства США

Примечания
Данные выборочные Внебиржевые котировки приводятся по операциям, не превышающим 1 млн. долл. Котировки векселей, нот и облигаций Казначейства США приводятся по состоянию на 12.00
3. Цены выражены в центах за 1 долл. от номинальной стоимости.
4. Цифры в 3-м и 4-м столбцах (после двоеточия) не являются сотой частью цента, а представляют собой значения, выраженные в 32-х долях. Таким образом 89:19 означает 89 и 19/32 (или 0,8959375 долл.), а не 0,8919 долл.
Данные, содержащиеся в табл. 8.2, показывают, что цена предложения на казначейские стрипы с датой погашения в мае 2000 г. составляла 89 и 19/32 (89,59375) центов за доллар номинала. Для казначейских стрипов с датой погашения в мае 2027 г. цена предложения составляла 17 и 31/32 (или 17,96875 центов за доллар номинала).
В табл. 8.3 частично представлен курсовой бюллетень по облигациям Казначейства США, взятый из TheWallStreetJournal. Он отличается от предыдущего бюллетеня тем, что в первом столбце здесь показаны купонные ставки по каждой облигации. Буква п после месяца погашения, указывает на то, что облигация является нотой (note) Казначейства США. Это означает, что срок погашения этой облигации менее 10 лет.

8.5. ПОЧЕМУ ЦЕННЫЕ БУМАГИ С ОДИНАКОВЫМИ СРОКАМИ ПОГАШЕНИЯ МОГУТ ИМЕТЬ РАЗЛИЧНУЮ ДОХОДНОСТЬ

Часто можно обнаружить, что две облигации Казначейства США с одинаковыми сроками погашения имеют различную доходность при погашении. Является ли это нарушением закона единой цены? Ответ: нет. На самом деле, в применении к облигациям, имеющим различные купонные ставки, закон единой цены подразумевает, что если кривая доходности не является постоянной, то облигации с одинаковыми сроками погашения будут иметь различную доходность при погашении3.

8.5.1. Влияние купонной доходности

Рассмотрим, например, две различные купонные облигации со сроком погашения два года. Одна купонная облигация имеет купонную доходность 5%, а другая — 10%. Предположим, что текущие рыночные цены и доходности годичных и двухгодичных купонных облигаций соответствуют следующим значениям.

В соответствии с законом единой цены денежные платежи по каждой купонной облигации за первый год должны составлять 0,961538 долл. за 1 долл. от номинальной стоимости облигации, а денежные платежи за второй год — 0,889996 долл. Таким образом, рыночная цена двух различных купонных облигаций будет следующей.
Для 5%-ной купонной облигации:
0,961538 х 50 долл. + 0,889996 х 1050 долл. = 982,57 долл. Для 10%-чой купонной облигации:
0,961538 х 100 долл. + 0,889996 х 1100 долл. = 1075,15 долл.
Теперь рассчитаем значения доходности при погашении по каждой купонной облигации, которые будут соответствовать этим рыночным ценам. Для 5%-ной купонной облигации.

Для 10%-ной купонной облигации.

Таким образом, для того, чтобы соответствовать закону единой цены, две облигации должны иметь различную доходность при погашении. Отсюда вытекает следующее общее правило.
Если кривая доходности не является постоянной, то облигации с одинаковыми сроками погашения, но различными купонными ставками будут иметь различные показатели доходности при погашении.

8.5.2. Влияние риска дефолта и налогообложения

Временами можно столкнуться с такой ситуацией, когда облигации с одинаково купонной доходностью и сроками погашения продаются по разной цене. Эти отклонения обусловлены влиянием на стоимость ценных бумаг других факторов, которые приводят к тому, что при всей своей внешней идентичности, они лишь кажутся одинаковыми.
Облигации, обеспечивающие одинаковый поток фиксированных денежных поступлений, могут отличаться по ряду причин. Однако наиболее существенными являются риск дефолта и условия налогообложения. В качестве примера рассмотрим облигацию, по которой предполагается выплата 1000 долл. по истечении одного года. Предположим, что процентная ставка по годичным облигациям Казначейства США составляет 6% в год. Эти, ценные бумаги не подвержены риску дефолта, и поэтому цена на такую облигацию будет составлять 1000 долл./1,06 = 943,40 долл. Однако, если существует хоть какой-нибудь риск дефолта (т.е. риск неплатежа), независимо от того насколько мал этот риск, цена такой облигации будет меньше 943,40 долл., а ее доходность будет выше 6% в год.
Уровень налогообложения облигаций может зависеть от того, кто является эмитентом или непосредственно от самого типа облигации. Все это, безусловно, влияет на стоимость облигаций. В США, например, доход, полученный по облигациям, выпушенными правительствами штатов и местными органами управления, освобождаются от федерального подоходного налога. При всех других сходных параметрах эта особенность делает такие облигации более привлекательными для налогоплательщиков, и по сравнению с другими сопоставимыми облигациями цена на них будет выше (а доходность соответственно ниже).

8.5.3. Другие причины, влияющие на доходность облигаций

Существует также множество других факторов, которые приводят к появлению различия в ценах между внешне идентичными ценными бумагами с фиксированным доходом. Проверьте свою интуицию на примере двух следующих отличительных особенностей, которые отражаются на стоимости и доходности облигаций. Проанализируйте, каким образом эти признаки влияют на повышение или понижение стоимости аналогичных облигаций, но не имеющих таких свойств.
1. Возможность досрочного выкупа (callability). Эта особенность дает эмитенту право выкупа своих облигаций до наступления окончательной даты их погашения. Такая облигация называется облигацией с правом выкупа (callable bond).
2. Конвертируемость (convertibility). Эта особенность дает владельцу облигации право обменять ее на заранее определенное количество акций той компании, которая выпустила эту облигацию. Облигация, имеющая такой отличительный признак, называется конвертируемой (convertible bond).

8.6. ВРЕМЯ И ДИНАМИКА ЦЕН ОБЛИГАЦИЙ

В этом разделе рассматривается изменение цен облигаций, которое вызывается изменением рыночных процентных ставок и собственно течением времени.

8.6.1. Фактор времени

Если бы кривая доходности имела постоянный уровень и рыночные процентные ставки оставались неизменными, цена на любые безрисковые дисконтные облигации течением времени непрерывно повышалась бы, а цена на любые премиальные — снижалась. Связано это с тем, что с течением времени дата погашения облигаций приближается, а на момент погашения их цена должна равняться номинальной стоимости. Таким образом, по мере приближения даты погашения, цена на дисконтные и премиальные облигации будет стремиться к своему номиналу. На рис. 8.3 приведена динамика цен на бескупонные дисконтные облигации со сроком погашения 20 лет.
Рассмотрим метод расчета цены облигации, принимая во внимание, что номинальная стоимость облигации равна 1000 долл., а доходность остается фиксированной на уровне 6% в год. Первоначально облигация имеет срок погашения 20 лет и ее цена составляет:

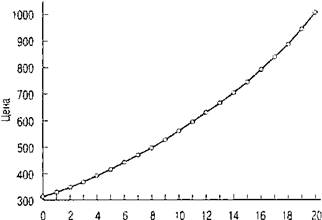
Время от даты выпуска облигации (лет)
Рис. 8.3. Динамика роста цены бескупонной облигации

Примечание: С течением времени при неизменной процентной ставке и равномерной структуре платежей цена бескупонной облигации будет расти со скоростью, эквивалентной ее доходности при погашении. График составлен из расчета номинала облигации 1000 долл. и 6% годовой доходности.
По истечении одного года со времени выпуска облигации до окончания ее срока погашения останется 19 лет и цена будет равна:

Таким образом, величина пропорционального изменения цены облигации точно соответствует ее доходности (6% в год):

Пропорциональное изменение цены = (330,51 долл. – 331,80 долл.) / 311,80 долл. = 6%

8.6.2. Процентный риск

Принято считать, что покупка долгосрочных облигаций Казначейства США со сроком обращения свыше 10 лет представляет собой консервативную инвестиционную политику, так как при этом отсутствует риск дефолта. Однако для инвесторов, вложивших в них средства, непредсказуемая экономическая среда с ее меняющимися процентными ставками, может принести как большие доходы, так и большие потери.
На рис 8.4 показана чувствительность цен долгосрочных облигаций к изменению процентных ставок. Этот график отражает динамику изменения цен на бескупонные дисконтные облигации со сроком погашения 30 лет и на купонные 8%-ные облигации с аналогичным сроком погашения. Предполагается, что сразу после их приобретения процентные ставки в экономике отклоняются от своего первоначального значения (8%). Каждая кривая представляет соответствующий ей тип облигаций. На оси OY нанесена шкала, показывающая коэффициент отношения цены облигации, рассчитанной исходя из переменного значения процентной ставки, к ее цене, рассчитанной по исходной 8%-ной ставке.

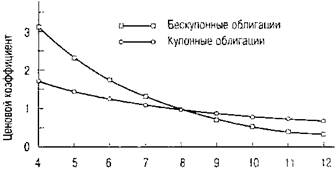
Процентная ставка (% в год)
Рис. 8.4. Чувствительность цены облигации к изменению процентных ставок

Допустим, что при процентной ставке 8% в год, цена 30-летней купонной облигации с номинальной стоимостью 1000 долл. равна 1000 долл. А уже при 9%-ной ставке ее цена равна 897,26 долл. Таким образом, отношение цены облигации при 9%-ной ставке к ее цене при 8%-ной ставке составит 897,26 / 1000 = 0,89726. Поэтому можно сказать, что если бы уровень процентных ставок поднялся с 8% до 9%, цена номинальной облигации упала бы примерно на 10%.
График описывает динамику изменения цен на бескупонные дисконтные облигации со сроком погашения 30 лет и на купонные 8%-ные облигации с аналогичным сроком погашения, если сразу после их приобретения процентные ставки отклонились бы от своего первоначального значения (8%). Значения оси OY представляют co-Sou отношение цены облигации, вычисленной по рассматриваемой процентной став- к ее цене, рассчитанной по исходной дисконтной 8%-ной ставке. Таким образом, при процентной ставке 8% соотношение цен для обеих облигаций составляет 1.
С другой стороны, при процентной ставке 8% в год цена 30-летней бескупонной облигации с номинальной стоимостью 1000 долл. равна 99,38 долл., а при 9%-ной Ставке ее цена равна 75,37 долл. Таким образом, отношение цены облигации при Ставке 9% к ее цене при 8%-ной ставке составляет 75,37 / 99,38 = 0,7684. Поэтому можно сказать, что если бы уровень процентных ставок поднялся с 8% до 9%, то цена купонной дисконтной облигации упала бы примерно на 23%.
Заметьте, что кривая, описывающая бескупонную дисконтную облигацию, более крутая, чем кривая, описывающая купонную облигацию. Это объясняется тем, что она более чувствительна к изменению уровня процентных ставок.

Резюме
• Изменение рыночных процентных ставок приводит к изменению в противоположном направлении рыночных цен всех существующих финансовых инструментов с фиксированными доходами.
• Вычисление текущей рыночной цены 1 долл., который предполагается получить в будущем, является исходным компонентом анализа фиксированных доходов по облигациям. Эта цена выводится на основании рыночных цен облигаций, которые в текущий момент времени обращаются на рынке. Затем полученные цены используются для оценки других фиксированных доходов.
• Еще один способ оценки стоимости облигаций заключается в использовании формулы расчета приведенной стоимости фиксированных поступлений с учетом различных дисконтных ставок для каждого определенного будущего периода времени.
• Отклонения в ценах на ценные бумаги с фиксированным доходом возникают в связи с различием в уровнях купонной доходности, наличием риска дефолта, особенностями, связанными с налогообложением, возможностью досрочного выкупа, конвертируемостью и другими факторами.
• По мере приближения даты погашения цена облигации будет приближаться к ее номиналу. Однако до наступления срока погашения цены могут значительно колебаться вследствие флуктуации рыночных процентных ставок.

Основные термины
• бескупонные облигации (pure discount bonds), 287
• нарицательная, номинальная стоимость облигации (face value),
287
• купонная, процентная облигация (coupon bond)
• купонная доходность (coupon rate)
• облигации, купленные по номиналу (par bonds)
• премиальная облигация (premium bond)
• текущая доходность (current yield)
• доходность при погашении (yield-to-matunty)
• облигация с правом выкупа (callable bond)
• конвертируемая облигация (convertible bond)

Ответы на контрольные вопросы
Контрольный вопрос 8.1. Что произойдет с курсом ценной бумаги с фиксированным доходом с ежегодной выплатой по ней 100 долл., если рыночная процентная ставка упаде 6% до 5% годовых?
ответ. Если процентная ставка упадет до 5% годовых, то курс ценной бумаги с фиксированным доходом возрастет до 272,32 долл.
Контрольный вопрос 8.2. Предположим, что доходность бескупонных облигаций со сроком погашения через 2 года упала до 6% в год, но остальные ставки, указанные в табл. 8 1, остались неизменными. Какова будет приведенная стоимость трехгодичного аннуитета по которому выплачивается 100 долл. в год? Какая единая дисконтная ставка, используемая в формуле приведенной стоимости, даст аналогичный результат?
ОТВЕТ. Стоимость трехлетнего аннуитета составит:
Приведенная стоимость ожидаемых поступлений за 1-й год = 100 долл. / 1,0526 =95,00 долл.
Приведенная стоимость ожидаемых поступлений за 2-й год = 100 долл. / 1,062 =89,00 долл.
Приведенная стоимость ожидаемых поступлений за 3-й год = 100 долл. / 1,07723 =80,00 долл.
Суммарная величина приведенной стоимости = 264 долл.
Таким образом, стоимость аннуитета возрастет на 1 долл.
Для того чтобы определить единую дисконтную ставку в соответствии с которой приведенная стоимость всех трех ожидаемых платежей равнялась бы 264 долл., необходимо использовать следующий вариант решения с помощью финансового калькулятора:

Контрольный вопрос 8.3. Какой будет текущая доходность и доходность при погашении трехлетней облигации, ценой приобретения 900 долл. и с купонной доходностью 6% в год?
ОТВЕТ. Текущая доходность составит —— = 0,067 = 6,67% Значение доходности при погашении рассчитывается следующим образом:

Контрольный вопрос 8.4. Используя те же самые цены, что и на бескупонные облигации, предложенные в предыдущем примере, определите цену и доходность при погашении двухгодичной купонной облигации с купонной доходностью 4% в год.
ОТВЕТ. Цена на облигацию с 4%-ной купонной доходностью равна:
0,961538 х 40 долл. + 0,889996 х 1040 долл. = 964,05736 долл. Доходность при погашении:

контрольный вопрос 8.5. Какой будет цена бескупонной облигации через два года, если годность зафиксируется на уровне 6% в год? Удостоверьтесь, что величина пропорционального изменения цены во втором году составит 6%.

ОТВЕТ. По истечении двух лет до окончания срока погашения останется 18 лет и цена облигации будет равна:

Таким образом, величина пропорционального изменения цены облигации точно соответствует ее доходности (6% в год):

Пропорциональное изменение цены = (350,34 долл. – 330,51 долл.) / 330,51 долл. = 6%

Контрольный вопрос 8.6. Предположим, что вы купили бескупонную облигацию с доходностью 6%, сроком погашения 30 лет и номиналом 1000 долл. На следующий день рыночные процентные ставки поднялись до 7%, что привело к повышению доходности вашей облигации до 7%. Какова будет величина пропорционального изменения цены облигации?
ОТВЕТ. Исходная цена бескупонной облигации со сроком погашения 30 лет равна:

На следующий день ее цена будет равна:

Величина пропорционального снижение цены составит 24,55%.

Вопросы и задания

Оценка облигаций с равномерной структурой платежей
ШаблонM8.1-8.3
1. Предположим, вам необходимо определить цену 7%-ной купонной о6-лигации Казначейства США со сроком погашения 10 лет с ежегодной выплатой процентов.
а. Вы узнали, что доходность при погашении составляет 8%. Какова будет цена облигации?
Ь. Какова будет цена облигации, если купонные платежи осуществляются раза в полгода, а доходность при погашении составляет 8%?
с. Теперь вы узнали, что доходность при погашении составляет 7% в год. Какая будет цена облигации? Можете ли вы предположить результат, не выполняя специальных расчетов? Что будет, если купонный доход будет выплачиваться раз в полугодие?
2. Предположим, шесть месяцев назад кривая доходности по ценным бумагам Казначейства США зафиксировалась на уровне 4% в год (с годовым начисление процентов) и вы купили облигацию Казначейства США со сроком погашения 30 лет. Сегодня кривая доходности вышла на уровень 5% в год. Какую доходность вы получили бы по своей первоначальной инвестиции:
а. если купили бы 4%-ную купонную облигацию?
Ь. если купили бы бескупонную облигацию?
с. насколько изменятся ваши ответы, если выплата по купонным платежам осуществляется раз в полгода?
Оценка облигаций с неравномерной структурой платежей
3. Предположим, вы изучаете следующие цены на безрисковые бескупонные облигации:

а. Какой должна быть цена на купонную облигацию с 6%-ной купонной доходностью и сроком обращения два года, если купонные платежи осуществляются один раз в год начиная со следующего года?
Ь. Впишите в таблицу отсутствующее значение.
с. Какой будет доходность при погашении по двухгодичной купонной облигации, рассматриваемой в пункте а)?
d. Почему ваши ответы для пунктов Ь) и с) отличаются друг от друга?
Отделение купонов
14. Предположим, вы искусственно хотите создать бескупонную облигацию со сроком погашения через два года. В вашем распоряжении имеется следующая информация: одногодичные бескупонные облигации продаются из расчета 0,93 долл. за один доллар от номинальной цены, а двухгодичные 7% купонные облигации (с ежегодной выплатой процентов) продаются по цене 985,30 долл. (номинал = 1000 долл.).
а. Какие два денежных поступления ожидаются по двухгодичной облигации?
Ь. Допустим, вы можете купить двухгодичную купонную облигацию и раздельно продать два денежных потока по этой облигации.
i. Сколько вы получите от продажи первого купонного платежа (отделенного купона)?
п. Какую сумму необходимо получить от продажи двухгодичной облигации Казначейства США с отделенными купонами для того, чтобы выйти на точку безубыточности своих инвестиций?
Закон единой цены и оценка облигаций
5. Предположим, что все облигации, указанные в следующей таблице, сопоставимы по всем ценовым параметрам, за исключением ожидаемых доходов. Используйте табличные данные и закон единой цены для расчета отсутствующих табличных значений. Купонные платежи осуществляются ежегодно.

Характерные особенности облигаций и их влияние на оценку облигаций
6. Каким образом следующие особенности отразятся на рыночной цене облигаций по сравнению с теми из них, которые не обладают такими свойствами.
а. Облигация со сроком погашения 10 лет может быть досрочно выкуплена компанией по истечении 5-летнего срока (облигация с правом выкупа). Сравните ее с 10-летней облигацией без права выкупа.
Ъ. Облигация является конвертируемой и может быть в любое время обменяна на 10 обычных акций. Сравните ее с неконвертируемой облигацией.
с. Облигация со сроком погашения 10 лет может быть возвращена компании (т.е. продана обратно эмитенту) по своей номинальной стоимости по истечении 3-х лет с момента выпуска. Сравните ее с аналогичной облигацией не имеющей права возврата.
d. Процентный доход по облигации с 25-летним сроком погашения освобожден от уплаты налогов.
Оценка гарантированных облигаций (выпущенных одной компанией и гарантированных другой)
7. Предположим, что кривая доходности по безрисковым долларовым облигациям, зафиксировалась на уровне 6% в год. Двухлетняя 10%-ная купонная облигация (с ежегодными купонными платежами и номинальной стоимостью 1000 долл.), выпущенная компанией DafaltoCorporation, имеет категорию риска Вив настоящее время продается по рыночной цене 918 долл. Кроме возможного риска неуплаты, облигации этой компании не имеют каких-либо других отличительных признаков. Какую сумму следовало бы заплатить инвестору за получение гарантии от возможного риска неуплаты по облигации Defalto Co.?
Оценка конвертируемых облигаций и облигаций с условием о досрочном выкупе
8. Предположим, что кривая доходности по безрисковым облигациям зафиксировалась на уровне 5% в год. Безрисковая купонная облигация со сроком погашения 20 лет (с номинальной стоимостью 1000 долл. и ежегодными купонными платежами), которая может быть досрочно выкуплена компанией-эмитентом по истечении 10-летнего срока, имеет купонную доходность 5,5% и котируется по своей номинальной стоимости.
а. Как можно оценить влияние на стоимость облигации наличия условия досрочного выкупа?
Ь. Облигация компании SafecoCorporation идентична во всех отношениях с 5,5%-ной купонной облигацией с правом досрочного выкупа, описание которой приведено выше. Однако она является конвертируемой, и в любое время до окончания срока своего погашения может быть обменена на 10 акций компании SafecoCorporation. Если доходность при погашении в настоящее время составляет 3,5% в год, то как можно оценить влияние на стоимость облигации наличия условия конвертируемости?
Изменения процентных ставок и цен на облигации
9. Если на протяжении всей кривой доходности (т.е. для всех ценных бумаг Казначейства) процентные ставки увеличиваются, то при всех прочих одинаковых условиях, следует ожидать того, что:
i. цены на облигации будут падать;
ii. цены на облигации будут расти;
iii. цена на долгосрочные облигации будет падать больше, чем цена на краткосрочные;
iv. цена на долгосрочные облигации будет расти больше, чем цена на кпят косрочные облигации;
а. правильными являются ответы ii и iv;
b. нельзя быть уверенным в том, что цены будут изменяться;
с. правильным является только ответ i;
d. правильным является только ответ ii;

Ваш комментарий о книге
Обратно в раздел Экономика и менеджмент